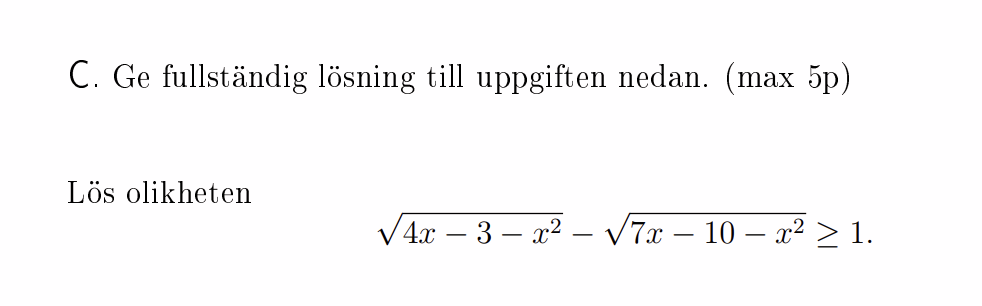Matematik- och fysikprovet 2024 – Lösningsförslag
I denna tråd finns lösningsförslag till matematikdelen av Matematik- och fysikprovet 2024. Då den tråd ConnyN och jag gjorde för provet som gavs 2022 blev både lång och ibland seg att öppna, är detta en samlingstråd, som länkar till varsin egen tråd för varje uppgift. Det möjliggör mer diskussioner kring olika lösningsförslag, utan att denna tråd blir extremt lång och klumpig.
Ställ gärna frågor eller bidra med egna lösningsförslag och strategier, i respektive tråd för varje fråga. :)
Uppgift 1:
Talen och är reella. Givet att , så gäller att är lika med
(a)
(b)
(c)
(d) inget av (a)-(c).
Uppgift 2:
Om och är reella tal så är villkoret "minst ett av talen a och b är skilt från 0" ekvivalent med
(a)
(b)
(c)
(d) inget av (a)-(c)
Uppgift 3:
Om x är ett reellt tal och , så gäller(a)
(b)
(c)
(d) inget av (a)-(c).
Uppgift 4:
Olikheten är ekvivalent med olikheten
(a)
(b)
(c)
(d) inget av (a)-(c).
Uppgift 5:
Alla lösningar till olikheten ges av
(a) alla negativa x och
(b) alla reella x
(c) alla negativa x och
(d) inget av (a)-(c)
Uppgift 6:
Om för alla reella tal x och y, så gäller för alla reella x och y att
(a)
(b)
(c)
(d) inget av (a)-(c) gäller generellt
Uppgift 7:
Antalet heltalslösningar till olikheten , där är ett reellt tal, är
(a) 0
(b) ändligt, skilt från 0
(c) oändligt
(d) kan ej avgöras
Uppgift 8:
Givet är ekvationen , där . Två av de tre koecienterna , , är reella och en är icke-reell. Då kan man dra slutsatsen att ekvationen inte är ekvivalent med någon ekvation , där
(a) alla tre koecienterna är reella
(b) alla tre koecienterna är icke-reella
(c) en koecient är reell och två av koecienterna är icke-reella
(d) inget av (a)-(c), den kan vara ekvivalent med ekvationer av alla tre typerna.
Uppgift 9:
Givet är ekvationen , där . Två av de tre koefficienterna , , är reella och en är icke-reell. Då kan man dra slutsatsen att
(a) en av ekvationens lösningar är reell och den andra icke-reell
(b) minst en av ekvationens lösningar är icke-reell
(c) minst en av ekvationens lösningar är reell
(d) inget av (a)-(c)
Uppgift 10:
Priset för en förpackning av en viss produkt har ökat med 10%, medan innehållets vikt har minskat med 10%. Kilopriset för produkten har då ökat med
(a) mindre än 20%
(b) exakt 20%
(c) mer än 20%
(d) det går inte att avgöra.
Uppgift 11:
Antalet reella lösningar till ekvationen för är
(a) 1
(b) 2
(c) kan ej avgöras
(d) inget av (a)-(c).
Uppgift 12:
För alla positiva reella tal x och y gäller att
(a)
(b)
(c)
(d) inget av (a)-(c) gäller generellt.
Uppgift 13:
För alla positiva reella tal x och p gäller att
(a)
(b)
(c)
(d) inget av (a)-(c) gäller generellt.
Uppgift 14:
Om och , så gäller att är lika med
(a)
(b)
(c)
(d) inget av (a)-(c) gäller generellt.
Uppgift 15:
Om och , så gäller att är lika med
(a)
(b)
(c)
(d) inget av (a)-(c) gäller generellt.
Uppgift 16:
Om , så gäller
(a)
(b)
(c)
(d) ingen av formlerna gäller generellt.
Uppgift 17:
Ekvationen , där koefficienterna och är reella tal, har lösningarna . Man kan då dra slutsatsen att
(a) både b och c är heltal
(b) minst ett av talen b och c inte är ett heltal
(c) varken b eller c är heltal
(d) inget av (a)-(c).
Uppgift 18:
En triangel har sidlängderna , och . Den minsta vinkeln i triangeln är då
(a) 30°
(b) skild från 30°
(c) det går inte att avgöra
(d) det finns ingen sådan triangel
Uppgift 19:
En triangel har sidlängderna , , längdenheter. Den minsta vinkeln i triangeln är då
(a) 30°
(b) skild från 30°
(c) det går inte att avgöra
(d) det finns ingen sådan triangel
Uppgift 20:
Givet är en tetraeder ABCD, sådan att |AB| = |AC| = |AD| = 2 längdenheter, och de tre plana vinklarna vid hörnet A är räta. Tetraederns höjd från hörnet A mot sidan BCD har i samma längdenheter längden
(a)
(b) annat tal
(c) det går inte att avgöra
(d) det finns ingen sådan tetraeder.
Uppgift 21:
BeräknaAnge svaret på formen , där , är heltal och bråket är maximalt förkortat.
Uppgift 22:
Bestäm alla reella tal , för vilka ekvationen har två icke-reella lösningar som befinner sig på avstånd 5 från talet 0. Ange det minsta talet med den egenskapen.
Uppgift 25:
En geometrisk talföljd har kvoten q. Bestäm de värden q kan ha givet att det andra elementet i följden är 1 och summan av de fyra första elementen i följden är 4. Ange summan av dessa värden.
Uppgift 26:
Lös ekvationen
.
Ange summan av de två minsta positiva lösningarna.
Uppgift 28:
I triangeln ABC gäller att l.e., l.e. Beräkna och ange längden av höjden från hörnet mot sidan .
Uppgift 29:
Två cirklar tangerar den räta linjen t och ligger på samma sida om den. Den ena cirkeln har medelpunkt och radie , den andra har medelpunkt och radie , där . Avståndet mellan de två medelpunkterna är . Linjen t skär linjen som binder samman cirklarnas medelpunkter i punkten . Beräkna och ange avståndet |. (Alla längder och avstånd mäts i samma längdenhet.)
Uppgift 30:
Romben ABCD har sidlängd (längdenheter). Summan av dess diagonallängder är (längdenheter). Beräkna och ange rombens area.
Finns det inget svar till C? 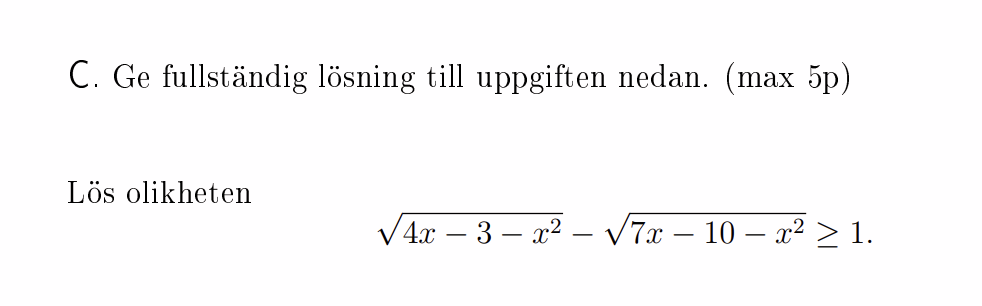
Volt skrev:Finns det inget svar till C?
Finns på deras hemsida