Hur ska man motivera att den största differensen b-a erhålls då b och a har samma avstånd?
Halloj!
Jag sitter med b)-uppgiften här:
Jag undrar hur man kan motivera att den största differensen erhålls då man låter och ligga lika långt ifrån symmetrilinjen . Jag har löst uppgiften på ett annat sätt men det hade inte funkat på ett prov. Jag skulle uppskatta ett direkt svar och inte en "ledning" som brukar vara praxis här, då jag är lite sent ute och inte förstår detta.
Antar att "brute-force" beräkning är den metod du använt och inte vill ha, denna kommer definitivt funka men tar förmodligen för lång tid på ett prov.
Ett annat intuitivt sett att direkt se det är genom att visualisera grafen till integranden. Det kommer vara en "ledsen" andragradsfunktion som skär x-axeln i 2 olika punkter. Det finns ett oändligt stort intervall för vilken integralen kommer vara negativ, men enbart ett ändligt intervall där integralen är positiv. Eftersom att integralen ska bli 0 vill vi balansera det negativa med det positiva. För att maximera avståndet mellan a och b vill vi inkludera hela det positiva området. Därmed kommer a och b vara på varsin sida om x=2 och x=5 som begränsar det positiva området.
Men varför just symmetriskt runt x=3.5 kan man undra? Det är eftersom att kurvan blir brantare ju längre ifrån denna symmetrilinje vi går. Detta innebär att för varje steg vi tar iväg från symmetrilinjen kommer integralen för det steget bli större och större. För att maximera avståndet mellan a och b vill vi att de går lika långt på båda sidor. Om antingen a eller b går längre ut på sin sida måste den andra gränsen kompensera genom att komma ännu närmre den första.
Ursäkta otydlig förklaring, har svårt att formulera det mycket bättre än såhär i textform. Hoppas du förstår ändå!
Tillägg: 16 maj 2024 23:13
Sista frågan, hur ska man komma på något sådant under ett tidsbegränsat prov?
Mitt tips är att börja med att visualisera funktionen i fråga. Det var så jag angrep denna uppgift och det gav mig bättre förståelse om vad som eftersöktes och hur man kan resonera sig fram till svaret.
Men jag förstår inte riktigt hur det resonemanget håller matematiskt. Man kan ju naturligtvis påstå att man måste gå åt båda hållen för att maximera avståndet, men ett annat alternativ vore ju att fixera och sedan gå tillräckligt långt till höger. Då kommer vi till slut få och få ett värde på .
Hur ska man veta att detta värde inte blir större än värdet på då man rör sig symmetriskt åt båda håll? Och hur kan vi resonera oss fram till att värdet på man får då man går åt båda håll blir det allra största, och att det inte finns någon annan variant som ger ett större värde?
Antar att "brute-force" beräkning är den metod du använt och inte vill ha, denna kommer definitivt funka men tar förmodligen för lång tid på ett prov.
Inte bara det, jag har noll aning hur jag skulle göra det på miniräknaren. Jag använde geogebra men det har vi ej tillgång till under provet :(
naytte skrev:Men jag förstår inte riktigt hur det resonemanget håller matematiskt. Man kan ju naturligtvis påstå att man måste gå åt båda hållen för att maximera avståndet, men ett annat alternativ vore ju att fixera och sedan gå tillräckligt långt till höger. Då kommer vi till slut få och få ett värde på .
Ursäkta som sagt för att jag formulerar mig otydligt, men det var där min poäng om lutningen kom in. Om vi fixar x=2 och ökar b tills C=0 kommer inte b komma särskilt långt eftersom att lutningen på funktionen ökar hela tiden så att integralen blir större (integralens ökning är snabbare än linjär). Så fort b har nått ett värde större en x=5 är det mer gynnsamt att minska a, tills 2-a > b-5. Sedan b osv fram och tillbaka. Väsentligen ökar/minskar vi båda gränserna samtidigt.
Skulle istället lutningen hos funktionen vara konstant kommer (b-a) vara densamma oavsett hur vi placerar gränserna på varsin sida om det positiva området.
Hur ska man veta att detta värde inte blir större än värdet på då man rör sig symmetriskt åt båda håll? Och hur kan vi resonera oss fram till att värdet på man får då man går åt båda håll blir det allra största, och att det inte finns någon annan variant som ger ett större värde?
Inte bara det, jag har noll aning hur jag skulle göra det på miniräknaren. Jag använde geogebra men det har vi ej tillgång till under provet :(
Går bra att räkna ut det för hand, men tar som sagt tid och inte rekommenderat att göra under provet.
Okej, insåg nu att det kanske inte funkar ändå. Hade en tanke om att det helt enkelt skulle reduceras till ett optimeringsproblem för variabeln (b-a) som inte skulle vara alltför svår att lösa analytiskt. Får skylla på trötthet just nu, om någon annan vill ta över och ro detta argument i hamn vore jag tacksam.
Oavsett vad är nog inte tanken att du ska använda denna metod. Skulle gissa på att lösningsförslaget mer eller mindre följer det resonemang jag skrev där uppe.
I dessa bedömda elevlösningar kan du få lite tips om vad som då ansågs vara tillräckligt bra motiveringar:


Du kan även läsa detta svar för en algebraisk lösning och en bit ner i denna tråd för ett försök till resonemang kring symmetrilinjen.
Så uppgiften gick från analytisk till 'CAS' på 1 år?
Ett par rader i Mathematica. Någon närmare utläggning om symmetrilinjer m.m. onödig;
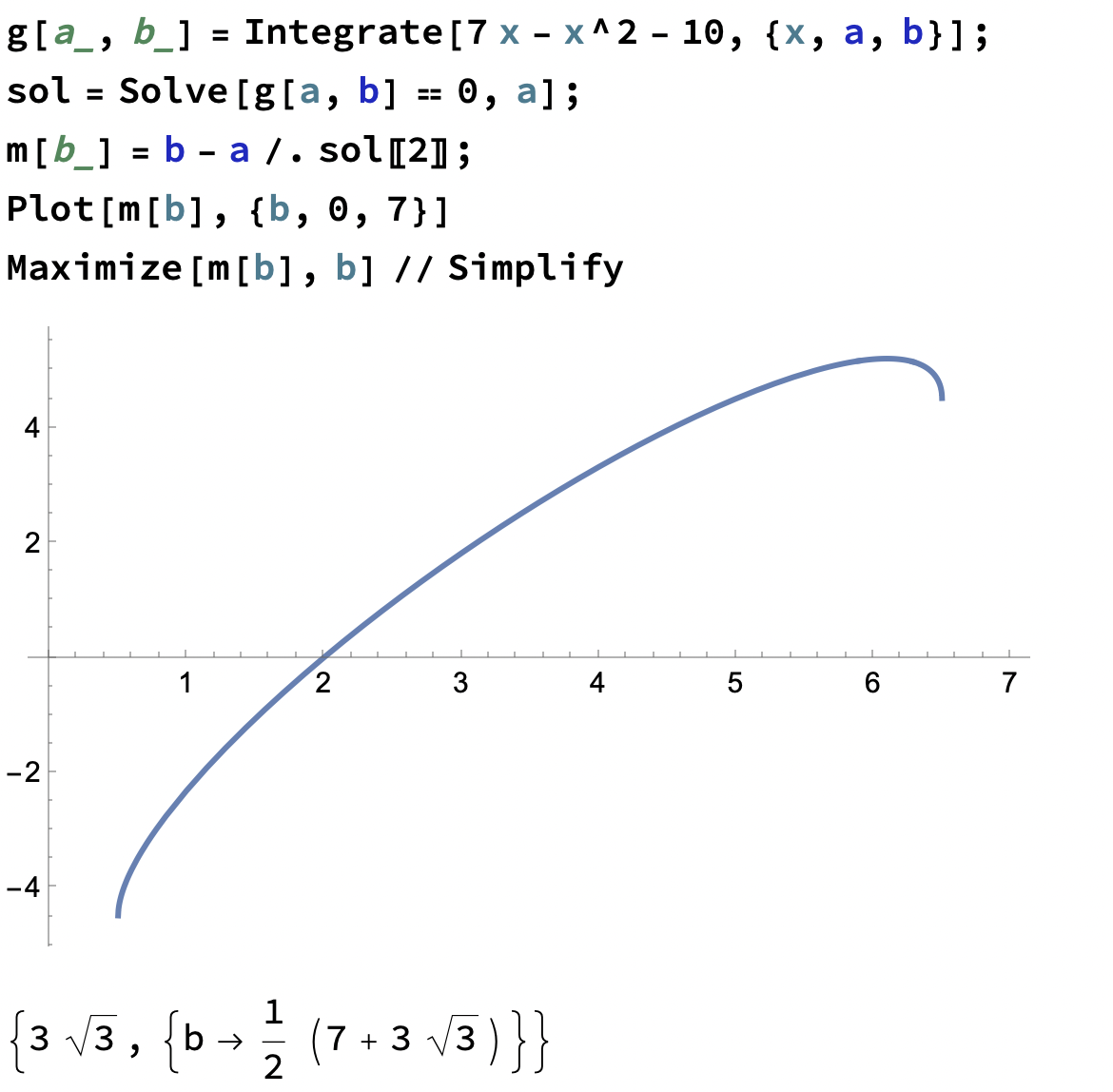
Fast den analytiska är "snyggare", men kräver "symmetrimotivering". Se dock #9 nedan.
Yngve skrev:Du kan även läsa detta svar för en algebraisk lösning och en bit ner i denna tråd för ett försök till resonemang kring symmetrilinjen.
I första tråden antar personen redan symmetri. Med det antagandet räcker det med att integrera från 3.5 till k och likställa med 0. Det leder till en tredjegradsekvation som vi kan lösa på valfritt sätt.
Vore intressant om vi kunde behålla problemet generellt. I slutändan kommer det oavsett leda till någon tredjegradare som ska lösas. Kan kika lite mer på det imorn om jag får tid.
Calle_K skrev:Yngve skrev:Du kan även läsa detta svar för en algebraisk lösning och en bit ner i denna tråd för ett försök till resonemang kring symmetrilinjen.
I första tråden antar personen redan symmetri. Med det antagandet räcker det med att integrera från 3.5 till k och likställa med 0. Det leder till en tredjegradsekvation som vi kan lösa på valfritt sätt.
Vore intressant om vi kunde behålla problemet generellt. I slutändan kommer det oavsett leda till någon tredjegradare som ska lösas. Kan kika lite mer på det imorn om jag får tid.
Kanske något i denna stil, där många beräkningar hoppats över, men fullt möjliga att utföra för hand;


Trinity2 skrev:Så uppgiften gick från analytisk till 'CAS' på 1 år?
Nej, tvärtom. CAS-lösningen är från en bedömd elevlösning 2022. Själva uppgiften är från NP Matte 4 vt22 där digitala hjälpmedel är tillåtna, men det visste jag inte förrän nu.
Tack, Trinity för din analytiska lösning utan solver!
@Yngve
Jag gjorde på samma sätt som personen i lösningsförslag #2. Men det första lösningsförslaget känns otillräckligt. Personen har ju knappast motiverat varför man kan göra så, utan har bara påstått att det är så. Och det kanske räcker för uppgiften. Men det känns bara omatematiskt.
Trinity2 skrev:Calle_K skrev:Yngve skrev:Du kan även läsa detta svar för en algebraisk lösning och en bit ner i denna tråd för ett försök till resonemang kring symmetrilinjen.
I första tråden antar personen redan symmetri. Med det antagandet räcker det med att integrera från 3.5 till k och likställa med 0. Det leder till en tredjegradsekvation som vi kan lösa på valfritt sätt.
Vore intressant om vi kunde behålla problemet generellt. I slutändan kommer det oavsett leda till någon tredjegradare som ska lösas. Kan kika lite mer på det imorn om jag får tid.
Kanske något i denna stil, där många beräkningar hoppats över, men fullt möjliga att utföra för hand;
Där har vi det. Mycket bra!
naytte skrev:@Yngve
Jag gjorde på samma sätt som personen i lösningsförslag #2. Men det första lösningsförslaget känns otillräckligt. Personen har ju knappast motiverat varför man kan göra så, utan har bara påstått att det är så. Och det kanske räcker för uppgiften. Men det känns bara omatematiskt.
Det stämmer. Och eleven fick ju inte heller full poäng för lösningen.
Vill bara meddela att jag skrev NP idag och att det gick väldigt bra! Tror faktiskt jag satte varje fråga, både på miniräknardelen och delen utan räknare, förutom en liten delfråga jag slarvade på 🥳🥳!
naytte skrev:Vill bara meddela att jag skrev NP idag och att det gick väldigt bra! Tror faktiskt jag satte varje fråga, både på miniräknardelen och delen utan räknare, förutom en liten delfråga jag slarvade på 🥳🥳!
Bravo! Vi håller tummarna för ett bra resultat.
naytte skrev:Vill bara meddela att jag skrev NP idag och att det gick väldigt bra! Tror faktiskt jag satte varje fråga, både på miniräknardelen och delen utan räknare, förutom en liten delfråga jag slarvade på 🥳🥳!
Redan de gamla romarna: Errare est humanum!
Jag instämmer med Yngves förhoppning!
Just det "Att mänskla är feligt" 😀
naytte skrev:Halloj!
Jag sitter med b)-uppgiften här:
Jag undrar hur man kan motivera att den största differensen erhålls då man låter och ligga lika långt ifrån symmetrilinjen . Jag har löst uppgiften på ett annat sätt men det hade inte funkat på ett prov. Jag skulle uppskatta ett direkt svar och inte en "ledning" som brukar vara praxis här, då jag är lite sent ute och inte förstår detta.
Vi skall maximera G(a, b) = b - a, under bivillkoret att C(a, b) = . Där p(x) är det givna polynomet i problemtexten
Låt oss antaga att (a, b) är den punkt som maximerar G med uppfyllt bivillkor.
Låt oss se vad som händer om vi gör infinitesimala förändringar da och db av variablerna a och b.
dC = . Om vi kräver att våra infinitesimala ändringar inte får bryta mot bivillkoret så måste dC = 0. Dvs
p(b)db - p(a)da = 0 (1).
Vidare så har vi att
dG = db - da.
Om G(a, b) är optimalt så måste dG vara noll. Antag tex att db - da är större än noll, men då skulle de infinitesimala ändringarna leda till en liten ökning av G, som då inte kan vara maximal. Om db - da är negativt så kan vi istället byta da mot -da och db mot -db och få ett positivt dG. Så dG måste vara noll. Dvs vi har kravet att
db - da = 0 (2).
Notera att både (1) och (2) måste var uppfyllda. Vi sätter in (2) i (1).
(p(b) - p(a))da = 0.
Om detta skall vara uppfyllt för godtyckliga da, så måste vi ha att p(a) = p(b).
Detta är uppfyllt om a = b (uppenbarligen inte max) eller om a och b ligger på samma avstånd från symmetrilinjen x = 7/2.
Vi kan bestämma värdet på b genom att kräva att
0 = , vilket ger att b = 7/2 + .
max(b - a) blir därmed .








