En spiral ritas med hjelp av halvcirklar
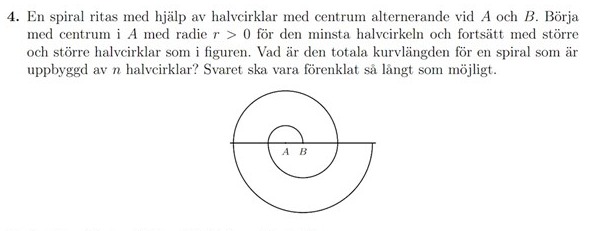
Hej! Klurar med uppgiften ovan. Har insett att det rör sig om en geometrisk summa då n rör sig mot oändligheten. Jag fick svaret men jag inser nu att det kanske inte går att anta att radien ökar med ? Om jag inte får göra så är jag helt vilse!
Jag såg den frågan här för ett litet tag sedan, men nu hittar jag den inte.
Längden är väl:
Vi bryter ut:
Den där summan ser välbekant ut.
Vad tror du om det och kommer du vidare?
Här är den: https://www.pluggakuten.se/trad/rakna-ut-total-kurvlangd
men ni har kanske kommit lika långt här.
Laguna skrev:Här är den: https://www.pluggakuten.se/trad/rakna-ut-total-kurvlangd
men ni har kanske kommit lika långt här.
Ungefär ja, men tack ändå.
sictransit skrev:Längden är väl:
Vi bryter ut:
Den där summan ser välbekant ut.
Vad tror du om det och kommer du vidare?
ska det stå k + 1 i parantesen och så ska n gå mot oändligheten? Eller är det inga gränsvärden som ska blandas in?
swaggerdabber44 skrev:sictransit skrev:Längden är väl:
Vi bryter ut:
Den där summan ser välbekant ut.
Vad tror du om det och kommer du vidare?
ska det stå k + 1 i parantesen och så ska n gå mot oändligheten? Eller är det inga gränsvärden som ska blandas in?
Frågan gäller ju längden för n halvcirklar, inte oändligt många.
Summan blir:
sictransit skrev:swaggerdabber44 skrev:sictransit skrev:Längden är väl:
Vi bryter ut:
Den där summan ser välbekant ut.
Vad tror du om det och kommer du vidare?
ska det stå k + 1 i parantesen och så ska n gå mot oändligheten? Eller är det inga gränsvärden som ska blandas in?
Frågan gäller ju längden för n halvcirklar, inte oändligt många.
Summan blir:
Jaha det förenklar det! Hur kom du fram till den summan?
swaggerdabber44 skrev:Jaha det förenklar det! Hur kom du fram till den summan?
Den är rätt allmänt känt, som pythagoras typ. Det sägs att Gauss briljerade när han som skolpojke blixtsnabbt summerade ihop de 1000 (?) första heltalen: Aritmetisk följd – Wikipedia
Hur som helst är det inte svårt att inse att summan av en aritmetisk talföljd är:
antalet tal * medelvärdet av det första och det sista
1+2+3+4+5 = 5 * (1+5)/2 = 15
sictransit skrev:swaggerdabber44 skrev:Jaha det förenklar det! Hur kom du fram till den summan?
Den är rätt allmänt känt, som pythagoras typ. Det sägs att Gauss briljerade när han som skolpojke blixtsnabbt summerade ihop de 1000 (?) första heltalen: Aritmetisk följd – Wikipedia
Hur som helst är det inte svårt att inse att summan av en aritmetisk talföljd är:
antalet tal * medelvärdet av det första och det sista
1+2+3+4+5 = 5 * (1+5)/2 = 15
Jag insåg nu att det var en aritmetisk talföljd! Ibland är det för lätt för att det ska bli uppenbart....Tack!



