Dubbelintegral
Behöver hjälp att förstå varför min lösning inte fungerar samt vad facit vill att man ska göra.
Detta är uppgiften: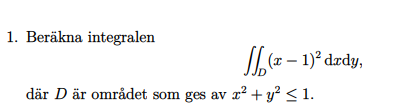 Såhär ser min lösning ut:
Såhär ser min lösning ut:
∫∫D(x-1)2
Enligt facit är svaret
Såhär löser dem det i facit:
Jag förstår inte hur de bryter ut , hur kommer in i integralen och varför de har .
Det här ser ut att vara samma uppgift: https://www.pluggakuten.se/trad/dubbelintegral-221
Är det phi du vill använda som parameter? Den där saken används vanligtvis bara i partiella derivator.
Laguna skrev:Det här ser ut att vara samma uppgift: https://www.pluggakuten.se/trad/dubbelintegral-221
Är det phi du vill använda som parameter? Den där saken används vanligtvis bara i partiella derivator.
Tack för svar.
Jag har lyckats förstå mig på facit och varför de gör som de gör, och varför det fungerar. Jag är dock fortfarande osäker på varför min lösning inte ger rätt svar.
Vad menar du med "phi som parameter"?
Din parametrisering ger inte rätt område. Den ger visserligen en enkel integrand.
Jag menar krumeluren som du t.ex. tar cos av. Ska det vara theta?
Laguna skrev:Din parametrisering ger inte rätt område. Den ger visserligen en enkel integrand.
Jag menar krumeluren som du t.ex. tar cos av. Ska det vara theta?
^ Ditt område blir fel då x = 1 + rcos(phi) sätter ditt område (cirkeln) ett steg ut längs x-axeln istället för kring origo, vilket x^2+y^2<=1 avser.


