Zooma in och ut i Chrome - ingen egentlig uppgift, bara en fundering

Notera att för t.ex. $a=\frac{1}{4}$ så skulle vi behöva att $5\cdot 3 bc=4^3$. Denna ekvation har inga lösningar eftersom VL är delbart med 5 och 3 men inte HL. Vad händer om du testar de andra värdena på $a$?

Då får jag

$$\begin{gathered} 15bc=4^3 \\ 45bc=4^3 \\ 75bc=4^3 \\ 75bc=4^2 \end{gathered}$$

Det är alltså hopplöst. Men, när jag ställer upp ekvationerna så här så känns det väldigt ointuitivt. Det ser ut som att ju mer jag zoomar, ju längre från målet kommer jag. Som att jag startat för långt ifrån, och bara kan köra ännu längre ifrån. Så är ju inte fallet - jag kan hålla på och komma lite över, lite under 100% zoom, fram och tillbaka.

Ok, problemet är ju med min ursprungliga uppställning. Ekvationen ska väl vara

$a\times {\left(\frac{5}{4}\right)}^b\times {\left(\frac{3}{4}\right)}^c=1$

Det är fortfarande hopplöst, men nu är det i alla fall vettigt med att man kan hamna omkring 1 istället för att komma längre och längre ifrån hela tiden.

thedifference skrev:

$a\times {\left(\frac{5}{4}\right)}^b\times {\left(\frac{3}{4}\right)}^c=1$

Det är fortfarande hopplöst, men nu är det i alla fall vettigt med att man kan hamna omkring 1 istället för att komma längre och längre ifrån hela tiden.

Fantastiskt kul tråd!

Följdfråga: Finns det någon gräns för hur nära du kan komma? Det vill säga: finns det en gräns för hur litet felet

$|\frac{1}{4}\cdot(\frac{5}{4})^b\cdot (\frac{3}{4})^c-1|$

kan bli genom att välja lämpliga positiva heltal $b$ och $c$?

oggih skrev:

thedifference skrev:

$a\times {\left(\frac{5}{4}\right)}^b\times {\left(\frac{3}{4}\right)}^c=1$

Det är fortfarande hopplöst, men nu är det i alla fall vettigt med att man kan hamna omkring 1 istället för att komma längre och längre ifrån hela tiden.

Fantastiskt kul tråd!

Följdfråga: Finns det någon gräns för hur nära du kan komma? Det vill säga: finns det en gräns för hur litet felet

$|\frac{1}{4}\cdot(\frac{5}{4})^b\cdot (\frac{3}{4})^c-1|$

kan bli genom att välja lämpliga positiva heltal $b$ och $c$?

Tråden i sig fick mig att tänka på denna serie. Speciellt nu när vi kommit till ett matematiskt moment som jag inte alls behärskar. Vi kan låtsas ett tag att det inte ens är uppfunnet.

oggih skrev:

thedifference skrev:

$a\times {\left(\frac{5}{4}\right)}^b\times {\left(\frac{3}{4}\right)}^c=1$

Det är fortfarande hopplöst, men nu är det i alla fall vettigt med att man kan hamna omkring 1 istället för att komma längre och längre ifrån hela tiden.

Fantastiskt kul tråd!

Följdfråga: Finns det någon gräns för hur nära du kan komma? Det vill säga: finns det en gräns för hur litet felet

$|\frac{1}{4}\cdot(\frac{5}{4})^b\cdot (\frac{3}{4})^c-1|$

kan bli genom att välja lämpliga positiva heltal $b$ och $c$?

Min intuition säger mig att det går, och det verkar även stämma när jag simulerar det. Men jag är inte säker på hur man kan visa det. Tänkte först på continued fractions och diofantisk approximering, men kan i princip inget om det. Har du något tips?

Om vi logaritmerar (övning till läsaren: gör detta!) så ser vi att det här är en variant av följande mer generella problem, som mycket riktigt hör till ett matematikområde som kallas för diofantisk approximering!

Problem: Givet två reella tal $x$ och $y$, kan vi approximera vilket tal $z$ som helst hur noggrant som helst, genom att ta lämpliga heltalslinjärkombinationer av $x$ och $y$? 

Svaret är ja, förutsatt att $x$ och $y$ är "oberoende", i bemärkelsen att kvoten $x/y$ inte är ett rationell tal (övning till läsaren: övertyga dig om varför detta är nödvändigt!).

Man brukar attribuera detta jakande svar till den tyska talteoretikern Dirichlet som levde på 1800-talet – och det går hyfsat enkelt att bevisa med lådprincipen som ofta uppkallas efter samma man!

Dirichlets approximationssats. Låt $x,y\in\mathbb{R}$ sådana att $\frac{x}{y}\not\in\mathbb{Q}$. Då gäller det att för varje $z\in\mathbb{R}$ och $\varepsilon>0$ så existerar det $b,c\in\mathbb{Z}$ sådana att $|bx+cy-z|<\varepsilon$.

Beviset med lådprincipen ger dock inte så mycket praktisk vägledning för hur man faktiskt ska hitta heltal $b$ och $c$ som gör jobbet. Därför:

Ny följdfråga: Är det kanske någon som kan mer om talteori och/eller programmering än mig som har något systematiskt sätt att göra detta på? Till exempel: Kan någon hitta $b$ och $c$ som ger

$|\frac{1}{4}\cdot(\frac{5}{4})^b\cdot (\frac{3}{4})^c-1|<\frac{1}{10\,000}$?

oggih skrev:

Ny följdfråga: Är det kanske någon som kan mer om talteori och/eller programmering än mig som har något systematiskt sätt att göra detta på? Till exempel: Kan någon hitta $b$ och $c$ som ger

$|\frac{1}{4}\cdot(\frac{5}{4})^b\cdot (\frac{3}{4})^c-1|<\frac{1}{10\,000}$?

Vad kul, här kunde jag hänga med igen! Skrev följande script i Python, som försöker 1 miljon gånger med att multiplicera med 5/4 om produkten är under 1 och med 3/4 om den är över, men slutar om vi kommer tillräckligt nära.

# for maximum precision
from decimal import Decimal

one = Decimal("1")
one_fourth = Decimal("0.25")
five_fourths = Decimal("1.25")
three_fourths = Decimal("0.75")
one_ten_thousandth = Decimal("0.0001")

b = 0
c = 0
product = one_fourth

for _ in range(1_000_000):
    if product < one:
        product *= five_fourths
        b += 1
    else:
        product *= three_fourths
        c += 1

    if abs(product - one) < one_ten_thousandth:
        print(b)
        print(c)
        print(one_fourth * (five_fourths) ** b * (three_fourths) ** c)
        break

För att komma så här nära behöver man bara blygsamma 1240 inzoomningar (b) och 957 utzoomningar (c). Detta ger oss talet 0.9999659327261617250174797267.

Wow! Snyggt jobbat! ^_^

Med det scriptet skulle vi kanske kunna undersöka detta:

Ny följdfråga: Kan man säga något om hur det totala antalet klick som behövs växer när vi minskar den tillåtna felmarginalen? Vad händer t.ex. om vi går till 0.0001, 0.00001 och så vidare?

Jag fick ganska exakt att felet minskade med en faktor 10 då jag ökade antalet iterationer med en faktor 10. Testade upp till 100 miljoner iterationer.

Hmm, det där låter inte direkt som en slump, så det går kanske att bevisa något här! ^_^

Var faktorn exakt 10? Kan du få printa ut några värden på b och c som algoritmen hittade?

oggih skrev:

Ny följdfråga: Kan man säga något om hur det totala antalet klick som behövs växer när vi minskar den tillåtna felmarginalen? Vad händer t.ex. om vi går till 0.0001, 0.00001 och så vidare?

Körde ett test där den skulle reagera på första kombinationen som kom nära nog. En miljard iterationer (där b eller c ökar med 1).

På 1E-9 blir det overflow på vad till och med Decimal klarar.

Kod:

# for maximum precision
from decimal import Decimal

one = Decimal("1")
one_fourth = Decimal("0.25")
five_fourths = Decimal("1.25")
three_fourths = Decimal("0.75")
target_arr = []

for i in range(8):
    dec_str = "0." + "0" * i + "1"
    my_decimal = Decimal(dec_str)
    target_arr.append(my_decimal)

b = 0
c = 0
product = one_fourth

to_remove = []

for _ in range(1_000_000_000):
    if product < one:
        product *= five_fourths
        b += 1
    else:
        product *= three_fourths
        c += 1

    # always start with the most lenient
    for target_distance in target_arr:
        if abs(product - one) < target_distance:
            print(f"Target distance: {target_distance}")
            print(f"b: {b}")
            print(f"c: {c}")
            print(f"Product: {one_fourth * (five_fourths) ** b * (three_fourths) ** c}")

            to_remove.append(target_distance)
        else:
            # if the most lenient wasn't close enough, the second won't be either, etc
            break

    # remove target distances we have already found the minimum for
    if to_remove:
        for remove_me in to_remove:
            target_arr.remove(remove_me)
        to_remove = []

    # we've found minimums for all distances and completed the test
    if not target_arr:
        break

Väldigt imponerande att Decimal-paketet kan hålla koll på alla de där decimalerna – och att Python kan genomföra en miljard iterationer så snabbt! ^_^

Jag provade att plotta dina värden i en log-log-plot och får något som ser anmärkningsvärt linjärt ut, vilket indikerar att $b+c$ beror på felmarginalen $\varepsilon$ som en potensfunktion (övning till läsaren: förstå varför potensfunktioner $y=kx^a$ ser linjära ut i en log-log-plot, och hur man kan avläsa $k$ och $a$ i en sådan plot).

Om vi passar en rät linje till datan så får vi att exponenten är ungefär $-1$, vilket skulle innebära att $b+c$ är ungefär omvänt proportionellt mot felmarginalen $\varepsilon$, vilket precis stämmer med Gustors observation här ovan! 

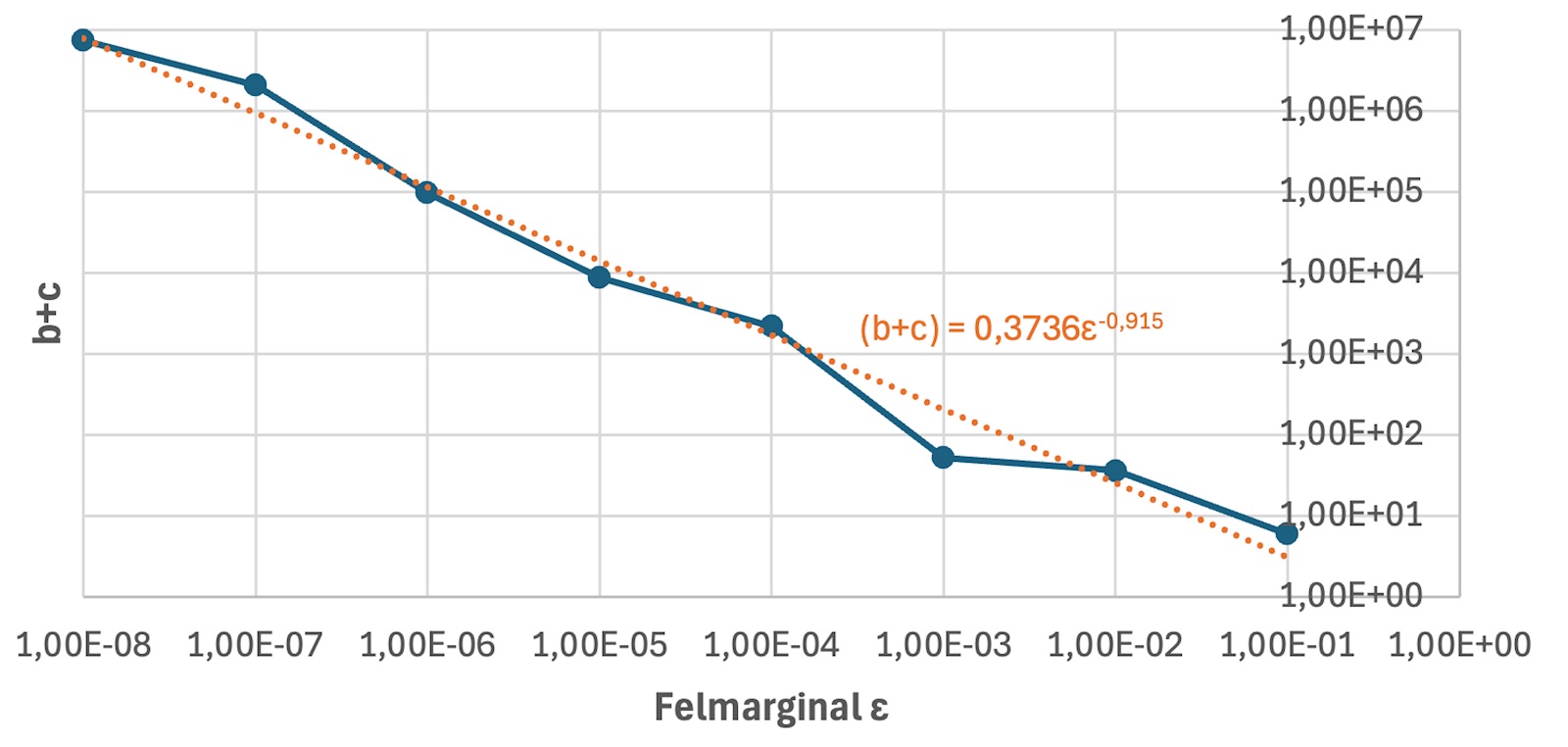
Jag funderar på om det är en slump $b+c$ beror på $\varepsilon$ på ett så strukturerat sätt här, eller om det är det mer generellt matematiskt fenomen som vi observerar! Om någon har tankar är jag idel öra!

Och rent experimentellt skulle nästa steg kanske kunna vara att undersöka om vi får liknande resultat för andra förändringsfaktorer än just $5/4$ och $3/4$.

Egentligen går det inte så snabbt med 1 miljard iterationer... den hittar bara det sista resultatet ganska snabbt och avbryter. För en del andra tar det lång tid, så jag har satt 1E-7 som sista. Här är tre andra med godtyckliga b och c.

a = 1/4 för samtliga.

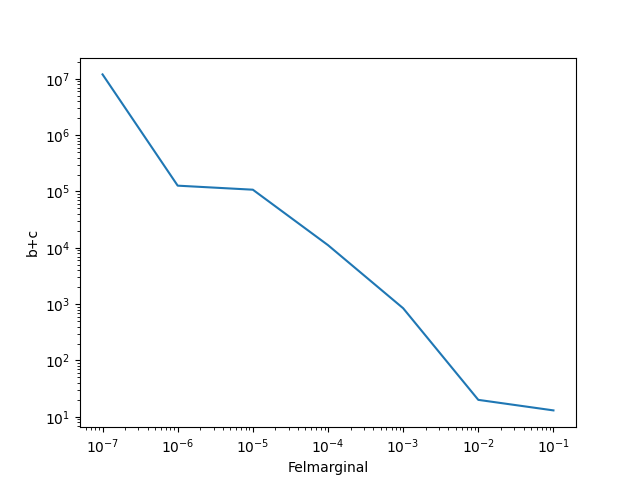
b = 17/8, c=1/5

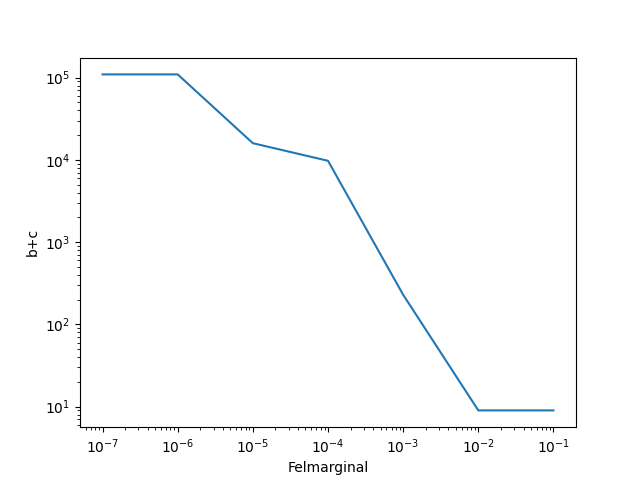
b=7/6 (decimalapproximerat), c=3/5

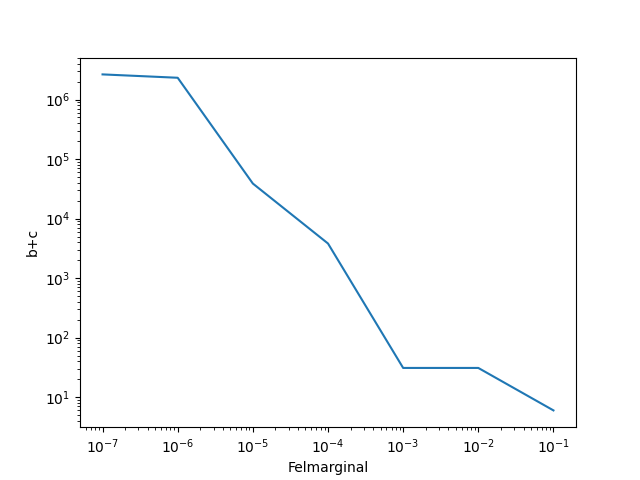
b=11/8 (decimalapproximerat), c=3/4

Eftersom jag har resultaten för den sista uppe kan jag tillägga att E-2 och E-3 båda klaras av 17, 14, och att de högsta två är nära men inte samma: 1 100 171, 1 217 845 samt 1 253 026, 1 387 050.

Har svårt att uttrycka mig om matten men vill du ha fler experiment i Python så är det bara att säga till =)