Zeta = max(xi1,xi2) beräkna p(0,3 <= zeta <=0,85)
Hej! Jag undrar hur de gjort för att beräkna sannolikheten? Enligt deras formel som de använder förstpr jag inte hur de gjort?
'Frågan:

Facit:
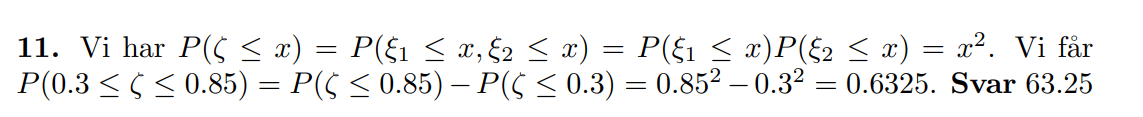
Hur jag tänker att det borde bli enligt formeln:

Tack på förhand!
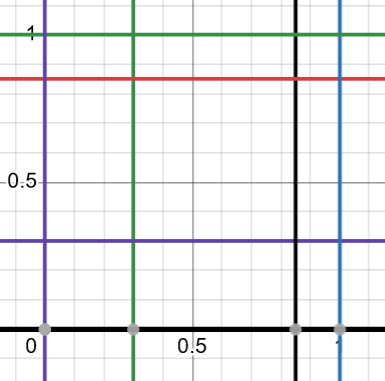
Utfallsrummet är kvadraten 0<x<1, 0<y<1. Den sökta sannolikheten är kvadraten 0,3<x<0,85, 0,3<y<0,85. Hur många % är den lilla kvadraten av den stora kvadraten?
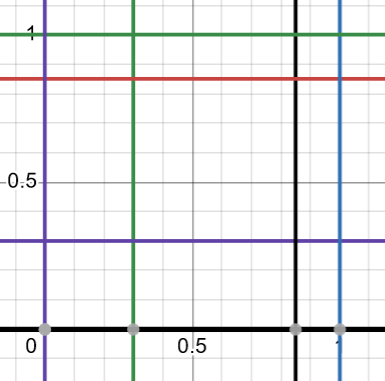
Smaragdalena skrev:Utfallsrummet är kvadraten 0<x<1, 0<y<1. Den sökta sannolikheten är kvadraten 0,3<x<0,85, 0,3<y<0,85. Hur många % är den lilla kvadraten av den stora kvadraten?
Den sökta sannolikheten inkluderar även de två rektanglarna 0<x<0.35, 0.35<y<0.85 samt 0.35<x<0.85, 0<y<0.35
Följande beräkning
P(0.35<X<0.85) = P(X<0.85-0.35)
hade fungerat om X var rektangelfördelat.
I detta fall är X = max(xi1, xi2) där xi1 och xi2 är rektangelfördelade, den stokastiska variabeln X blir inte rektangelfördelad.
Den sökta sannolikheten inkluderar även de två rektanglarna 0<x<0.35, 0.35<y<0.85 samt 0.35<x<0.85, 0<y<0.35
Ja tänk, det har du rätt i! Tack.