Xk = k/n?
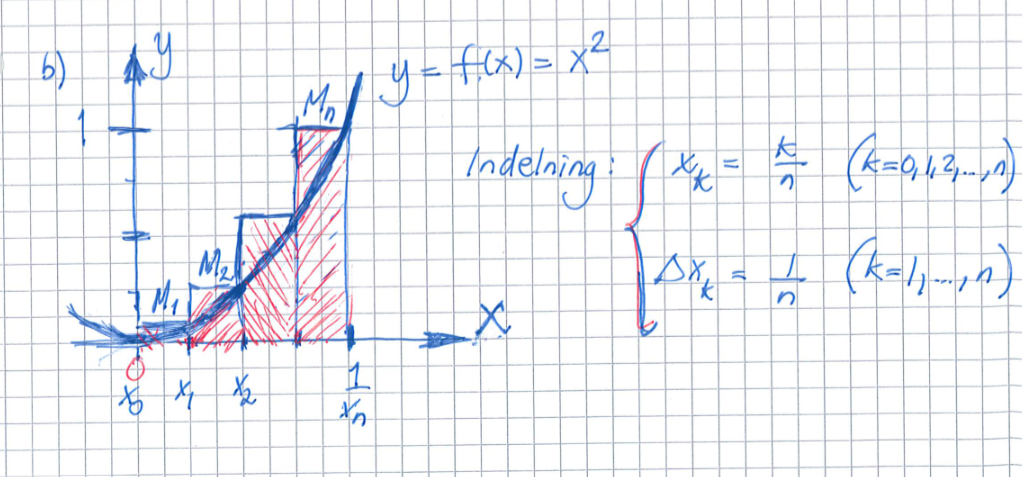
Hej! På b) funderar jag på hur de kom fram till att Xk = k/n och att maxf(x) = (k/n)^2?


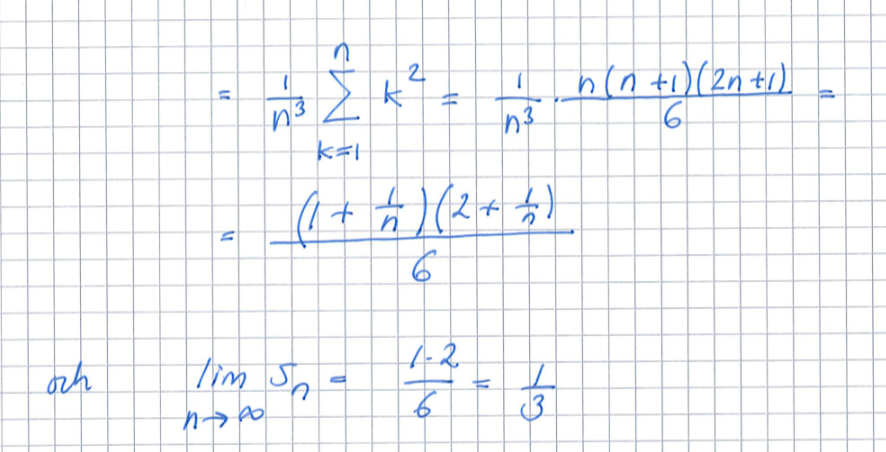
Tack på förhand!
Xk ska nog vara xk = x-koordinaten för det k:te delintervallet i dess högra ändpunkt. Eftersom f är strängt växande antas max för det k:te delintervallet just i dess högra ändpunkt. Därav max f(x)=(k/n)2.
Ah okej tack! men hur kommer de på att de sa dela k med n?
Om du skulle beräkna arean på en gräsmatta som begränsades av en kurva, så tror jag att också du skulle dela in arean i mindre och mer lättberäknade bitar. Idén här är förstås att låta rektanglarna bli så smala och många att rektanglarna kan ”ersätta” kurvan. Den här metoden funkar så länge som f är kontinuerlig och positiv. I definitionen av Riemann- integralen, som denna är, ingår också undersummor. Detta för att kunna handskas också med kurvor som dyker under x-axeln och kurvor som inte är kontinuerliga överallt. Dock får antalet diskontinuiteter bara vara ändligt i en Riemann-integral.
Ah okej tack!:)

