X går mot a
Hej
Jag har några funderingar kring gränsvärde:
Lim x->en siffra; går funktionen alltid mot oändligheten?
Lim x->0: går funktionen alltid mot ett tal?
Gränsvärdet Lim x->0 för sinx/x: kan jag använda den för 0+ och 0-? Tänker jag då att svaret som I vanliga fall blir 1 blir samma eller något annat?
Jag undrar också, uppgiften som jag gjorde där dessa frågor kom:
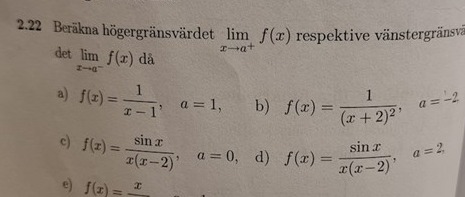
Jag gjorde a och c. Här är min lösning på a och c
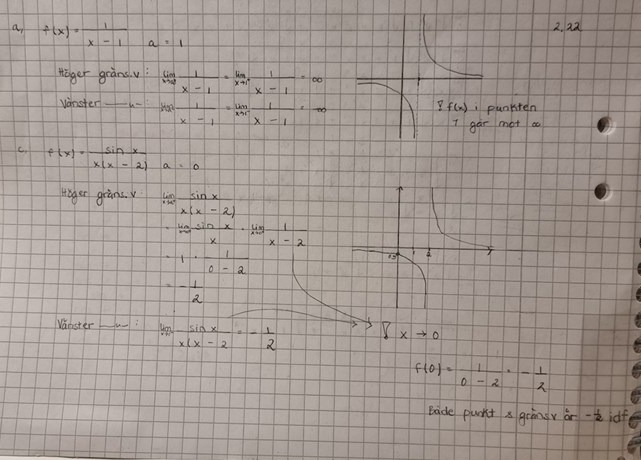
På a så tittar jag på ritningen och avgör, men på c så sätter jag in 0 för att få svaret: men om jag hade suttit in 1 i a så hade jag inte fått rätt svar. Hur ska jag tänka? När ska jag göra vad?
Lim x->en siffra; går funktionen alltid mot oändligheten?
Lim x->0: går funktionen alltid mot ett tal?
Gränsvärdet Lim x->0 för sinx/x: kan jag använda den för 0+ och 0-? Tänker jag då att svaret som I vanliga fall blir 1 blir samma eller något annat?
Nej, nej och ja.
På a så tittar jag på ritningen och avgör, men på c så sätter jag in 0 för att få svaret: men om jag hade suttit in 1 i a så hade jag inte fått rätt svar. Hur ska jag tänka? När ska jag göra vad?
Du hade inte ens kunnat sätta in i a), det är det som är den stora skillnaden. Ofta måste man manipulera uttrycket algebraiskt innan man faktiskt kan stoppa in värden.
naytte skrev:Lim x->en siffra; går funktionen alltid mot oändligheten?
Lim x->0: går funktionen alltid mot ett tal?
Gränsvärdet Lim x->0 för sinx/x: kan jag använda den för 0+ och 0-? Tänker jag då att svaret som I vanliga fall blir 1 blir samma eller något annat?
Nej, nej och ja.
På a så tittar jag på ritningen och avgör, men på c så sätter jag in 0 för att få svaret: men om jag hade suttit in 1 i a så hade jag inte fått rätt svar. Hur ska jag tänka? När ska jag göra vad?
Du hade inte ens kunnat sätta in i a), det är det som är den stora skillnaden. Ofta måste man manipulera uttrycket algebraiskt innan man faktiskt kan stoppa in värden.
Oh okej, men i c när jag har brutit ut så liknar den 1/(x-2) funktionen i a: här kan jag ju stoppa in 0 fast jag har inte gjort något med uttrycket. Varför är det så?
Jag vet inte riktigt vad jag ska svara på den frågan. Om du stoppar in i a) så får du ju en nämnare med 0. Dina fall i c) och a) är ju helt annorlunda.
naytte skrev:Jag vet inte riktigt vad jag ska svara på den frågan. Om du stoppar in i a) så får du ju en nämnare med 0. Dina fall i c) och a) är ju helt annorlunda.
Varför är det helt olika eller vad är det som är olika? Menar du olika värden jag stoppar i?
Heocon skrev:naytte skrev:Lim x->en siffra; går funktionen alltid mot oändligheten?
Lim x->0: går funktionen alltid mot ett tal?
Gränsvärdet Lim x->0 för sinx/x: kan jag använda den för 0+ och 0-? Tänker jag då att svaret som I vanliga fall blir 1 blir samma eller något annat?
Nej, nej och ja.
På a så tittar jag på ritningen och avgör, men på c så sätter jag in 0 för att få svaret: men om jag hade suttit in 1 i a så hade jag inte fått rätt svar. Hur ska jag tänka? När ska jag göra vad?
Du hade inte ens kunnat sätta in i a), det är det som är den stora skillnaden. Ofta måste man manipulera uttrycket algebraiskt innan man faktiskt kan stoppa in värden.
Oh okej, men i c när jag har brutit ut så liknar den 1/(x-2) funktionen i a: här kan jag ju stoppa in 0 fast jag har inte gjort något med uttrycket. Varför är det så?
0 kan du väl inte stoppa in utan göra något med uttrycket i c)?
Mrpotatohead skrev:Heocon skrev:naytte skrev:Lim x->en siffra; går funktionen alltid mot oändligheten?
Lim x->0: går funktionen alltid mot ett tal?
Gränsvärdet Lim x->0 för sinx/x: kan jag använda den för 0+ och 0-? Tänker jag då att svaret som I vanliga fall blir 1 blir samma eller något annat?
Nej, nej och ja.
På a så tittar jag på ritningen och avgör, men på c så sätter jag in 0 för att få svaret: men om jag hade suttit in 1 i a så hade jag inte fått rätt svar. Hur ska jag tänka? När ska jag göra vad?
Du hade inte ens kunnat sätta in i a), det är det som är den stora skillnaden. Ofta måste man manipulera uttrycket algebraiskt innan man faktiskt kan stoppa in värden.
Oh okej, men i c när jag har brutit ut så liknar den 1/(x-2) funktionen i a: här kan jag ju stoppa in 0 fast jag har inte gjort något med uttrycket. Varför är det så?
0 kan du väl inte stoppa in utan göra något med uttrycket i c)?
Men hur ska jag göra då? För når jag bara tittat på den så vet jag inte vad funktionen är vid ×=0. 0.5 kommer från att jag stoppa in 0
Vid x=0 är den odefinierad.
f(0)=sin(0)/(0*(0-2))
Bara för f(x) är odef i 0 betyder det inte att alla funktioner du kan bryta ur den, såsom 1/(x-2) måste vara odef där.
Din uträkning (-1/2) är ju korrekt.
Mrpotatohead skrev:Vid x=0 är den odefinierad.
f(0)=sin(0)/(0*(0-2))
Bara för f(x) är odef i 0 betyder det inte att alla funktioner du kan bryta ur den, såsom 1/(x-2) måste vara odef där.
Din uträkning (-1/2) är ju korrekt.
Vänta, om den är odefinerad i 0 så är jag med på den delen. Det blir som a uppgiften där 1 är odefinerad. Men varför räknar man inte de på samma sätt isf?
Heocon skrev:Mrpotatohead skrev:Vid x=0 är den odefinierad.
f(0)=sin(0)/(0*(0-2))
Bara för f(x) är odef i 0 betyder det inte att alla funktioner du kan bryta ur den, såsom 1/(x-2) måste vara odef där.
Din uträkning (-1/2) är ju korrekt.
Vänta, om den är odefinerad i 0 så är jag med på den delen. Det blir som a uppgiften där 1 är odefinerad. Men varför räknar man inte de på samma sätt isf?
Aha vänta jag fattar. För jag har delat på de så I den termen 0-2 blir den inte definierad. Okej nu är jag med. Tack🥹



