VT-19 DTK Uppgift 30

30. Hur många ridsportföreningar fanns det i genomsnitt per år under perioden 1990–2000?
A 750
B 850
C 950
D 1 050
Vet någon hur man kan hitta genomsnittet genom att rita en vågrät linje mellan år 1990 och år 2000 för y=750, y=850, y=950 och y=1050? Fick veta att man kan spara tid under högskoleprovet då, än att räkna ut areorna för figurerna och sen dividera med 10.

Tänk dig ett diagram med en rät linje – alla år är antalet föreningar exempelvis 150 stycken. Vilket är då det genomsnittliga antalet?
Tänk nu att grafen är en rät linje som börjar på noll och går till 300. Vilket är då det genomsnittliga antalet?
Hur är det om du har en kurva som pendlar mellan 200 och 400 – vartannat år är antalet 200, och vartannat år är antalet 400 – vilket är då genomsnittet? :)
Smutstvätt skrev:Tänk dig ett diagram med en rät linje – alla år är antalet föreningar exempelvis 150 stycken. Vilket är då det genomsnittliga antalet?
Då borde det genomsnittliga antalet vara 150? Jag har inte en bild av hur denna diagrammet ser ut i mitt huvud.
Tänk nu att grafen är en rät linje som börjar på noll och går till 300. Vilket är då det genomsnittliga antalet?
Är inte säker.
Hur är det om du har en kurva som pendlar mellan 200 och 400 – vartannat år är antalet 200, och vartannat år är antalet 400 – vilket är då genomsnittet? :)
300? Jag antar att man är intresserad av att arean under ska vara lika stor som arean ovanför, för att få det genomsnittliga värdet.
Då borde det genomsnittliga antalet vara 150? Jag har inte en bild av hur denna diagrammet ser ut i mitt huvud.
Precis! Jag har tagit mig friheten att rita upp dessa exempel som diagram. Detta exempel ser ut såhär:

(linjen går vid 150) Här är snittet 150, eftersom värdet varje år är 150.
Exempel två, ser ut såhär:
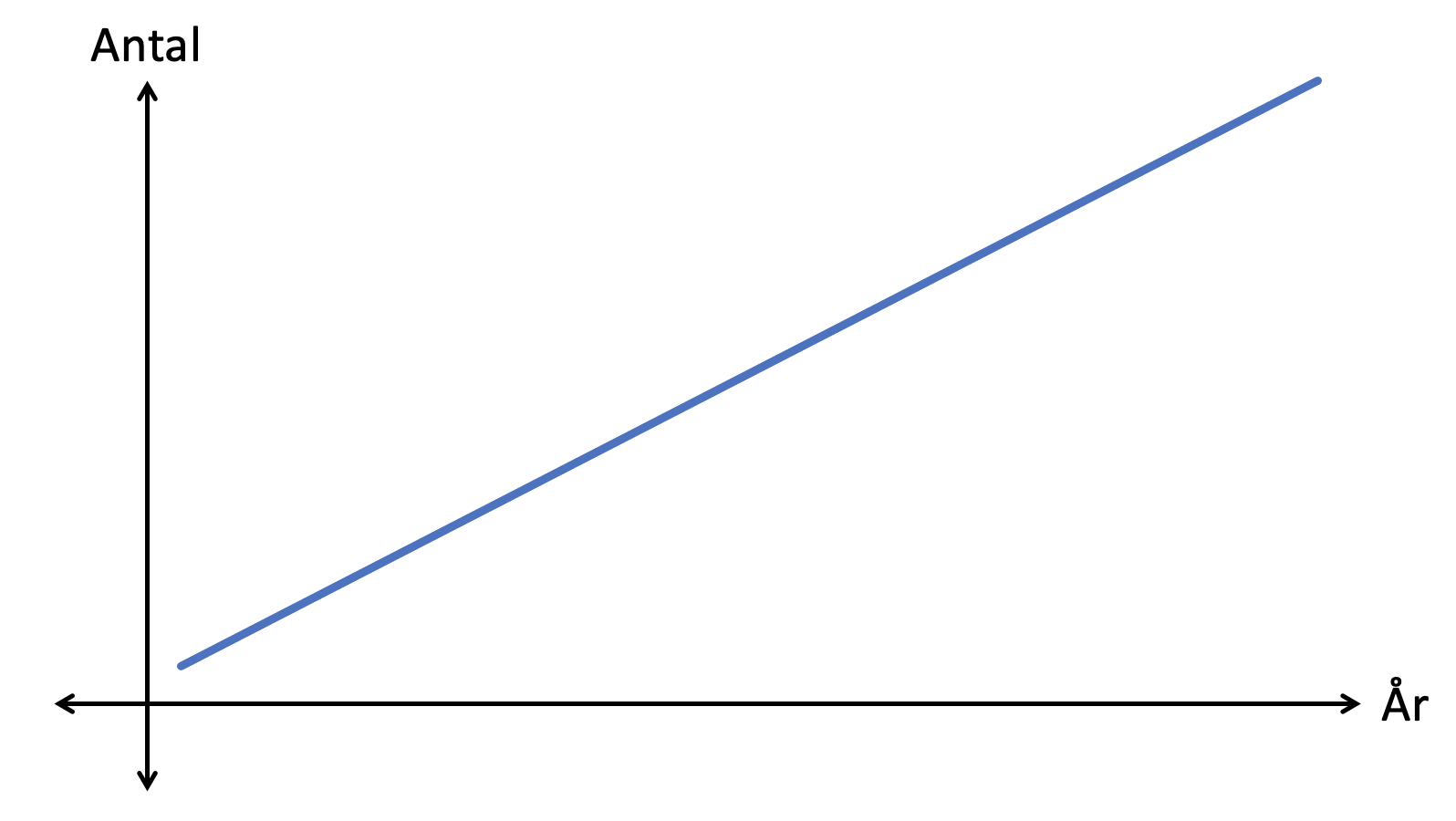
Då går snittlinjen i mitten av värdena. Se den streckade linjen nedan:

I det tredje exemplet, när du skriver:
300? Jag antar att man är intresserad av att arean under ska vara lika stor som arean ovanför, för att få det genomsnittliga värdet.
Har du helt rätt!
Kurvan ser ut såhär:

När du skriver
Jag antar att man är intresserad av att arean under ska vara lika stor som arean ovanför, för att få det genomsnittliga värdet.
Är du helt rätt ute! Vi vill pussla om värdena så att vi får en helt vågrät linje, som i exempel ett, eftersom vi då vet vad genomsnittet är (om alla värden är lika stora, är snittet det värdet). Jag har satt ihop ett litet klipp som visar ungefär hur en kan tänka (men eftersom det är en filmsnutt har jag laddat upp den på imgur). Vi ritar in det värde vi tror är vårt snitt (på HP är detta de olika svarsalternativen). Sedan ser vi om areorna ovanför och under grafen verkar ta ut varandra, eller om det finns för mycket ovanför eller under grafen. I detta exempel är snittet ganska lagom – det är lite för mycket ovanför grafen egentligen, men förhoppningsvis framgår konceptet i alla fall. :)


