volymberäkning runt y=3
Formen hos en viss kropp kan beskrivas genom att området i första kvadranten som begränsas av linjerna y=3 och x=3 och kurvan y=x2 + 4 roteras runt linjen y= 3 .Beräkna kroppens volym.
Jag förstår inte riktigt hur jag ska räkna ut det när området roteras y=3.
Jag vet att man kan beräkna det genom pi*∫x^2dy, vilka integrationsgränser ska jag ha?
Skissa kroppen så blir det ganska tydligt för dig.
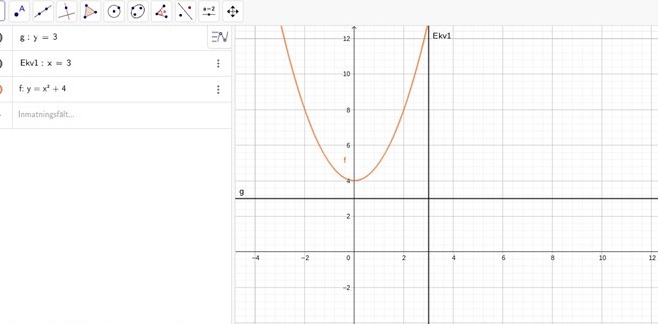
så ser det ut men är det så att kurvan begränsas av y-axeln?
Som vanligt, rita upp kroppen!
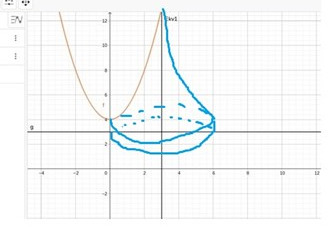
ska det inte roteras runt y=3 ?
Jo, du har rätt! Jag läste fel.
Det är alltså detta område som roterar runt linjen y = 3:

hur ska jag göra då för att jag har både y=3 och x=3
Pröva att göra en grov skiss av hur området roterar runt y = 3.
Markera gärna även hur en skiva ser ut och vad den har för radie.
Visa din skiss så hjälper vi dig vidare.
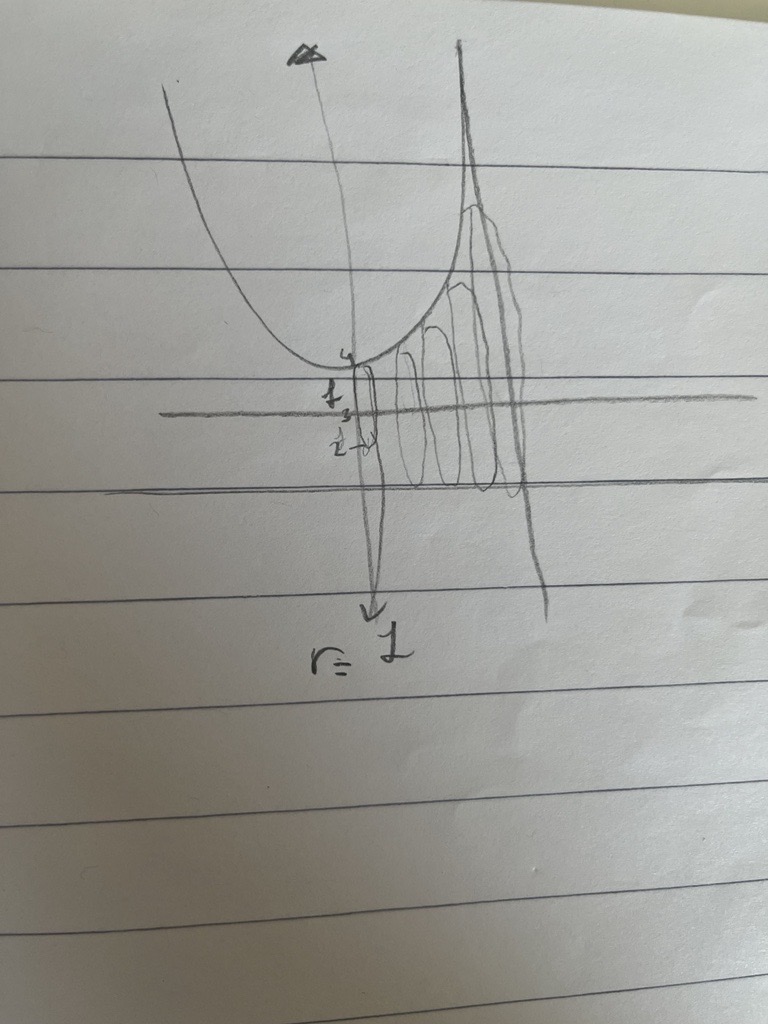
något sånt...
Snyggt!
Jag lade till lite förtydliganden.

Varje skiva har alltså en radie r och en tjocklek dx.
Med hjälp av radien kan du ta fram ett uttryck för varje skivas area och detta multiplicerat med dx ger varje skivas volymbidrag.
Det finns ett samband mellan radien r och positionen x, vilket gör att du kan uttrycka radien med hjälp av x.
Skivorna ligger staplade på varandra längs med linjen y = 3, från x = 0 till x = 3, vilket ger dig tips om hur integralen ska sättas upp.
Kommer du vidare då.




