Visa logisk ekvivalens mellan definitioner av kontinuitet - infinitesimaler

Du definierar en Infinitesimal som ”ett objekt vars belopp är strikt större än 0 men strikt mindre än alla positiva tal”

Din definition stödjer sig alltså på begreppet Belopp, underförstått absolutbeloppet, dvs metriken på R. Men denna funktion har definitionsmängden R, så man kan inte stoppa in några andra objekt än reella tal där. Du behöver alltså en ny metrik.

Jag ville bara förklara det på ett sätt som var enkelt att förstå. Egentligen har jag en helt ny ordningsrelation på min mängd, tillsammans med den euklidiska metriken. Den vanliga ordningsrelationen på $\mathbb{R}$ är en delmängd till min nya ordningsrelation.

Definitionen av en infinitesimal följer implicit av denna definition:

$\displaystyle f(\varepsilon)\prec g(\varepsilon)\iff\exists a\in\mathbb{R}[f(x)< g(x)\;\;\forall x\in(0,a)]$

$\varepsilon$ är "grundinfinitesimalen". Hela talmängden bygger först på en algebraisk utvidgning med ett nytt objekt "$\varepsilon$". Sedan får detta objekt topologisk mening med hjälp av denna definition.

Jag har lite en känsla av att ekvivalensen inte gäller, att den förutsätter sluten definitionsmängd för funktionen.

Eller så förstår jag inte hur dina infinitesimaler fungerar.

Hmm, hur menar du det? 

Definitionen med $\sim$ säger att "om x ligger oändligt nära a ligger f(x) oändligt nära f(a)" och det är ju det epsilon-delta säger också, men på ett lite annorlunda sätt. 

Kan du till exempel visa att f(x)=1/x är kontinuerlig enligt infinitesimal definitionen?

Ja, i alla punkter som ingår i dess domän. Det är nog bara att välja ett $x=a+\alpha$, där $\alpha$ är någon infinitesimal. Då $x=a+\alpha$ ser vi per definition att $x\sim a$. Det är uppenbarligen sant att:

$\displaystyle \frac{1}{a+\alpha} \sim \frac{1}{a}$, ty $\displaystyle \frac{1}{a+\alpha}-\frac{1}{a}=\frac{a}{a(a+\alpha)}-\frac{a+\alpha}{a(a+\alpha)}=-\frac{1}{a(a+\alpha)}\cdot\alpha$

Produkten längst till höger är uppenbarligen infinitesimal eftersom $\alpha$ är infinitesimalt. Det innebär att för alla $x$ där $\displaystyle x \sim a$ följer att $\displaystyle f(x) \sim f(a)$. Det betyder per definition att funktionen är kontinuerlig i alla punkter där den är definierad.

Nä men jag tänker om a är infinitesimal.

Då tänker vi alltså att 1/epsilon och 1/(2*epsilon) ligger nära varandra. Då är jag inte säker på att jag förstår hur metriken fungerar här.

Definitionsmängden här är x>0 så innehåller epsilon, 2*epsilon osv.

Jag var nog otydlig i mitt ursprungsinlägg. $a$ i det här fallet är ett tal som ingår i den reella definitionsmängden, dvs. den "vanliga" definitionsmängden till funktionen. Eftersom $0$ inte är ett sådant tal för $1/x$ blir $1/\varepsilon$ lite meningslöst i det här sammanhanget.

Ok då är jag med

Den utvidgade domänen till reella tal >0 är alltså inte reella tal och infinitesimaler > 0 utan reella tal >0 och infinitesimaler som befinner sig oändligt nära något reellt tal >0? Dvs exklusive infinitesimaler>0 om de ligger oändligt nära 0?

Då stämmer det nog, ska fundera på bevis.

"utan reella tal >0 och infinitesimaler som befinner sig oändligt nära något reellt tal >0?"

Ja, alltså den utvidgade domänen inkluderar den vanliga domänen, samt alla (linjär)kombinationer av infinitesimaler och tal ur den vanliga domänen. Mejkar det sense?

Så om vi betraktar $1/x$ skulle exempelvis $x=1+\varepsilon$ ingå i den utvidgade domänen, men inte $x=0+\varepsilon$ eftersom 0 inte ingår i den vanliga domänen.

Så om $x\in D_f$ så gäller för _alla_ $x\sim a$ att $f(x)\neq f(a)$?

Edit: Vad jag tycker är konstigt är alltså att du inte valt en ekvivalensrelation samt att somliga kontinuerliga reella funktioner inte är kontinuerliga. Låt t.ex. $f(x)=1$. Då antar jag att du menar att $f(a)=f(x)$ samt att $f(x)-f(a)=0$ för alla $x$?

D4NIEL skrev:

Så om $x\in D_f$ så gäller för _alla_ $x\sim a$ att $f(x)\neq f(a)$?

Edit: Vad jag tycker är konstigt är alltså att du inte valt en ekvivalensrelation samt att somliga kontinuerliga reella funktioner inte är kontinuerliga. Låt t.ex. $f(x)=1$. Då antar jag att du menar att $f(a)=f(x)$ samt att $f(x)-f(a)=0$ för alla $x$?

Hoppsan, jag missade tydligen ännu en detalj i mitt inlägg. I mitt arbete har jag skrivit så här:

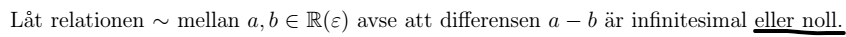
Redigerar genast ursprungsinlägget.

Man får då lägga till ett ytterligare krav tror jag. Vi får säga något i stil med detta istället:

$(\forall x \in D_f)[x\sim a \wedge x≠a \implies f(x) \sim f(a)]$

Nämen för mig känns det fortfarande som att det fattas saker här. 

Eller jag menar det här är ganska enkelt att bevisa i icke-standard analys på det sätt icke-standard analys presenterats för mig.

Som jag förstår det försöker du utvecklas någon egen typ av icke-standardanalys? Där man börjar med en algebraisk utvidgning av de reella talen? Så att man får något liknande de komplexa talen, a+b*e där e är infinitesimal istället för a+bi där i är imaginär? Är det som är idén?

Jag tänker att i en sådan kontext förstår jag inte hur en funktion agerar på infinitesimala objekt. Liksom ta den klassiska diskontinuerliga funktionen: indikatorfunktionen för irrationella tal. Vad är f(epsilon)?  

Eller jag menar det här är ganska enkelt att bevisa i icke-standard analys på det sätt icke-standard analys presenterats för mig.

Jodå, i gängse icke-standardanalys är det bara att använda transfer så är man färdig. Väldigt fint faktiskt, men sådan logisk lyx har jag tyvärr inte tillgång till.

Som jag förstår det försöker du utvecklas någon egen typ av icke-standardanalys? Där man börjar med en algebraisk utvidgning av de reella talen? Så att man får något liknande de komplexa talen, a+b*e där e är infinitesimal istället för a+bi där i är imaginär? Är det som är idén?

Ja typ, men istället för $a+b\varepsilon$ får man snarare något som liknar polynom med olika heltalspotenser av $\varepsilon$, sedan kan man gå vidare därifrån för mer komplexa funktioner som exponentialfunktioner m.m.

Jag tänker att i en sådan kontext förstår jag inte hur en funktion agerar på infinitesimala objekt. Liksom ta den klassiska diskontinuerliga funktionen: indikatorfunktionen för irrationella tal. Vad är f(epsilon)?  

Det saknar mening för mina infinitesimaler. Mina infinitesimaler kan inte vara irrationella eller rationella, på samma sätt som jag misstänker att de kan vara i vanlig icke-standardanalys med hjälp av transfer.

naytte skrev:

Eller jag menar det här är ganska enkelt att bevisa i icke-standard analys på det sätt icke-standard analys presenterats för mig.

Jodå, i gängse icke-standardanalys är det bara att använda transfer så är man färdig. Väldigt fint faktiskt, men sådan logisk lyx har jag tyvärr inte tillgång till.

Som jag förstår det försöker du utvecklas någon egen typ av icke-standardanalys? Där man börjar med en algebraisk utvidgning av de reella talen? Så att man får något liknande de komplexa talen, a+b*e där e är infinitesimal istället för a+bi där i är imaginär? Är det som är idén?

Ja typ, men istället för $a+b\varepsilon$ får man snarare något som liknar polynom med olika heltalspotenser av $\varepsilon$, sedan kan man gå vidare därifrån för mer komplexa funktioner som exponentialfunktioner m.m.

Jag tänker att i en sådan kontext förstår jag inte hur en funktion agerar på infinitesimala objekt. Liksom ta den klassiska diskontinuerliga funktionen: indikatorfunktionen för irrationella tal. Vad är f(epsilon)?  

Det saknar mening för mina infinitesimaler. Mina infinitesimaler kan inte vara irrationella eller rationella, på samma sätt som jag misstänker att de kan vara i vanlig icke-standardanalys med hjälp av transfer.

Nämen i standard icke-standard analys så är det här lätt att visa, även utan transfer.

Jo i "standard icke-standard" analys kommer varje infinitesimal utvärdera till 0 eller 1, som om de vore rationella eller irrationella (men i många fall  är det omöjligt att avgöra om 0 eller 1).

Jag känner ändå att det blir oklart nu: för vilka funktioner finns det en meningsfull utvidgning? Du pratar om polynom, exponentialfunktioner osv. Då är det nästan som att kontinuiteten är inbakad i vilka funktioner som har en utvidgning till att innefatta infinitesimaler. Någonstans så får vi ett så vekt funktionsbegrepp. Vilka diskontinuerliga funktioner har ens en utvidgning, bara de styckvis kontinuerliga?

Vad är det vi ska visa här då, att ekvivalensen gäller för de funktioner som har en meningsfullt utvidgning till infinitesimaler?

Nämen i standard icke-standard analys så är det här lätt att visa, även utan transfer.

Hur då? Jag har bara sett bevis där man är tvungen att använda transfer.

Vilka diskontinuerliga funktioner har ens en utvidgning, bara de styckvis kontinuerliga?

Jag har faktiskt inte funderat så mycket på detta. Men ett exempel skulle vara t.ex:

$\displaystyle f\left(x \right)=\frac{x^2-4}{x-2}$

Denna är varken kontinuerlig eller styckvis definierad, men skulle ha en meningsfull utvidgning.

Vad är det vi ska visa här då, att ekvivalensen gäller för de funktioner som har en meningsfullt utvidgning till infinitesimaler?

Jo, det är ju en förutsättning att vi ska kunna tolka vad funktionen är för att kunna tolka huruvida den är kontinuerlig.

naytte skrev:

Nämen i standard icke-standard analys så är det här lätt att visa, även utan transfer.

Hur då? Jag har bara sett bevis där man är tvungen att använda transfer.

Vilka diskontinuerliga funktioner har ens en utvidgning, bara de styckvis kontinuerliga?

Jag har faktiskt inte funderat så mycket på detta. Men ett exempel skulle vara t.ex:

$\displaystyle f\left(x \right)=\frac{x^2-4}{x-2}$

Denna är varken kontinuerlig eller styckvis definierad, men skulle ha en meningsfull utvidgning.

Vad är det vi ska visa här då, att ekvivalensen gäller för de funktioner som har en meningsfullt utvidgning till infinitesimaler?

Jo, det är ju en förutsättning att vi ska kunna tolka vad funktionen är för att kunna tolka huruvida den är kontinuerlig.

Alltså den funktionen är ju kontinuerlig. överallt där den är definierad. Återigen: om man ska visa den här ekvivalense behöver man ha en klar idé om hur utvidgningen av funktionen går till vid verkliga diskontinuiteter. Jag kan inte i alla fall inte hjälpa dig för jag vet inte exakt hur detta funkar.

Jag ska fundera vidare över exakt hur utvidgningen av domänerna borde se ut, och återkommer när jag har gjort det. Jag trodde inte det var så viktigt - i värsta fall bevisar man det för något bredare än det man behöver - men du har nog en poäng.

Men jag undrar ändå hur man kan bevisa ekvivalensen i gängse icke-standardanalys. Du nämnde att man kunde göra det utan transfer, vilket gör mig väldigt nyfiken, för hittills har jag bara sett bevis med transfer. Skulle du kunna skissera ett sådant bevis eller länka ett?

Jag var kanske kaxig, hemmansnickrat bevis on the fly, hoppas du inte hittar fel i det.

Men ungefär så här:

Antag först infinitesimal kontinuitet gäller i en reell punkt c. Antag sedan att $\epsilon -\delta$-kontinuitet inte gäller.

Negationen till ε-δ kontinuitet kan skrivas:

$\exists \epsilon :\forall \delta :\exists x\in \left[c-\delta .c+\delta \right]:\left|f\right(x)-f(c\left)\right|\ge \epsilon$

För detta $\epsilon$  konstruerar vi en serie ${\delta }_i=1/i$ och för varje i väljer vi ett lämpligt $x_i$.

Sätt sedan $x=x_1,x_2,...$. och $c=c,c,c,....$.

Vi har då att:

$x-c =x_1-c,x_2-c,...⩽1,1/2,1/3...$

så infinitesimalt, dvs x ligger oändligt nära c.

Men

$f\left(x\right)-f\left(c\right)=f\left(x_1\right)-f\left(c\right), f\left(x_2\right)-f\left(c\right),...\ge \epsilon ,\epsilon ,\epsilon ...$

Så större än $\epsilon$ och därför inte infinitesimalt. 

Vilket är motsägelse eftersom vi antog infinitesimal kontinuitet.

Andra riktningen är enklare, jag kan posta vid tillfälle

Andra riktningen:

Antag $\epsilon -\delta$-kontinuitet i en reell punkt c och att $x=x_1,x_2...$ ligger oändligt nära c.

För varje givet $\epsilon$ finns då ett $\delta$ sådant att osv...

Eftersom x ligger oändligt nära c har vi också:

$M_{\delta }=\{n:| x_n-c|<\delta \}\in F$

där F är vårt filter. Av vanliga kontinuiteten följer nu:

$M_{\epsilon }=\{n:|f( x_n)-f\left(c\right)|<\epsilon \}\supset M_{\delta }$

Så av filtrets superset-egenskap följer att  även $M_{\epsilon }$  tillhör F dvs $\left|f\right(x)-f(c\left)\right|<\epsilon$

för varje epsilon, dvs f(x) ligger oändligt nära f(c).

Angående ditt första bevis: har du inte krångligt till det lite med kvantifikationen av variablerna? Egentligen borde det väl stå så här:

$\displaystyle (\exists\varepsilon\in\mathbb{R}^+)(\forall \delta \in\mathbb{R}^+)(\exists x\in\mathbb{R})[x\in[c-\delta,x+\delta]\implies|f(x)-f(c)|\ge \varepsilon]$

Hoppas jag skrev det rätt nu som ett logiskt påstående. Hur som helst antar vi i negationen till $\varepsilon$-$\delta$-kriteriet att $\varepsilon$, $\delta$, och $x$ är reella tal. Men du drar sedan slutsatsen att $x-c$ är infinitesimalt, vilket omöjligen kan stämma om både $x$ och $c$ är reella. Jag tror du har använt transfer där utan att märka det. Det verkar som att beviset förutsätter att om negationen gäller för reella tal gäller den också för hyperreella tal, dvs. transfer.

Jag borde kanske varit tydligare med notationen, använt boldade bokstäver eller någonting.

x och c i epsilon-delta defintionen är förstås positiva reella tal.

Men sedan konstruerar vi de hyperreella talen:

$\mathit{x}=x_1,x_2,x_3,...$

och

$\mathit{c}=c,c,c,...$

'Det är differensen mellan de hyperrella x och c som är infinitesimal.

Men sen nej, din omformuleringen av negationen av epsilon-delta kriteriet är felaktig, f(x)-f(a)>epsilon behöver bara gälla ett x i intervallet, inte alla.

f(x)-f(a)>epsilon behöver bara gälla ett x i intervallet, inte alla.

Är det inte det jag skriver när jag skriver $\exists x...$? Då påstår jag väl bara att det finns ett sådant $x$, sådant att om $x\in[c-\delta, c+\delta] \implies |f(x)-f(c)|\ge \varepsilon$?

Det är differensen mellan de hyperrella x och c som är infinitesimal.

Borde det inte stå $f^*$ då när du skriver ut $f(x)-f(c)$? Det vill säga att vi jobbar med den hyperreella utvidgningen av $f$? Det är väl differensen $f^*(x)-f^*(c)$ vi kollar på då, medan det ursprungliga påståendet berör $f(x)-f(c)$?

naytte skrev:

f(x)-f(a)>epsilon behöver bara gälla ett x i intervallet, inte alla.

Är det inte det jag skriver när jag skriver $\exists x...$? Då påstår jag väl bara att det finns ett sådant $x$, sådant att om $x\in[c-\delta, c+\delta] \implies |f(x)-f(c)|\ge \varepsilon$?

Det är differensen mellan de hyperrella x och c som är infinitesimal.

Borde det inte stå $f^*$ då när du skriver ut $f(x)-f(c)$? Det vill säga att vi jobbar med den hyperreella utvidgningen av $f$? 

På första nej, det ska i så fall vara ett och, inte en implikation.

På andra, absolut, jag har slarvat lite med notationen.

Ja okej, jag förstår beviset, tror jag!

Vi har ju antagit att $f$ är mikrokontinuerlig vid $x=c$, dvs. $x \approx c \implies f(x) \approx f(c)$, men vi ser att $f^*(x)-f^*(c) \ge \varepsilon$. Och eftersom $\varepsilon$ är reellt kan det inte stämma. Vilket betyder att grundantagandet att $f$ är mikrokontinuerlig men inte $\varepsilon$-$\delta$-kontinuerlig samtidigt är falskt?

Jo precis så, det är egentligen hemskt enkelt.

Japp, verkligen! Jag ska se om jag kan formulera något liknande för mina tal, tack så mycket för beviset!

Jag har dessutom funderat en del på vilka typer av utvidgade domäner och målmängder jag kan ha i min definition. Jag sov på saken och kom fram till att det är rimligt att göra på följande sätt:

Låt $f : X \to Y$ vara en reellvärd, analytisk funktion. Beteckna dess taylorutveckling, centrerad runt $x=a$ som:

$\displaystyle g\left( x\right) = \sum_{n=0}^{\infty}\frac{f^n(a)}{n!}\left(x-a\right)^n$

Vi säger att den utvidgade domänen är mängden av alla tal $x\in\mathbb{R}_\varepsilon$, för vilken $g(x)$ är definierad i mitt ramverk. Kalla denna nya mängd $X_\varepsilon$. Den utvidgade målmängden $Y_\varepsilon$ är bilden av $X_\varepsilon$ under $g$.

Mitt algebraiska ramverk tillåter (i princip) samma typer av tal som gängse icke-standardanalys gör. Så t.ex. finns det saker som $\varepsilon^{\varepsilon^3\sqrt2}$. 

Jag tror ett rimligt krav är att funktionen ska vara analytisk för att det ska finnas en utvidgning. Det blir inte heller alltför begränsande eftersom de flesta funktionerna i analysen är analytiska, men samtidigt förlorar vi tyvärr möjligheten att tala om fulare funktioner som indikatorfunktionen.