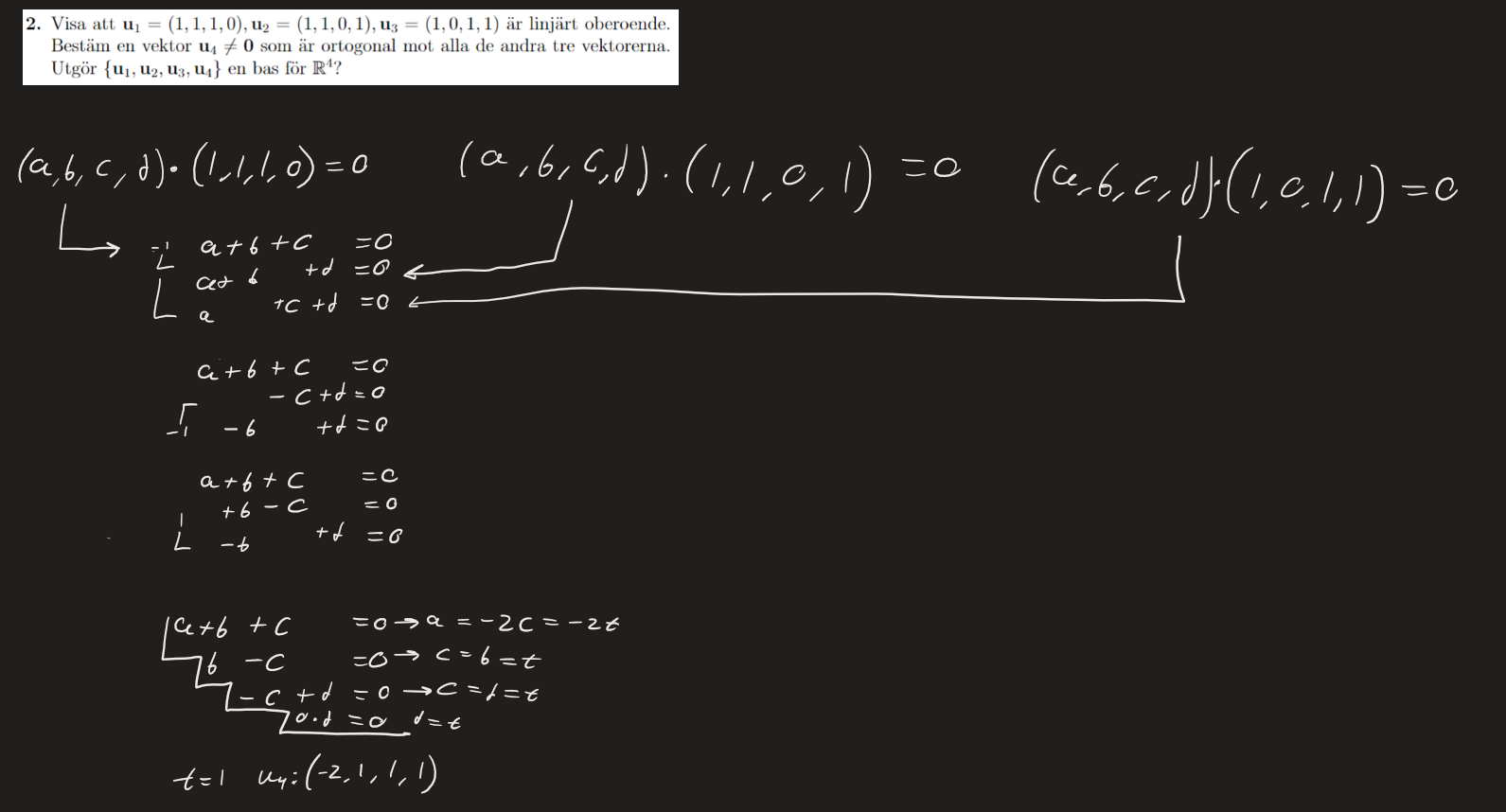
Visa att vektorerna är linjärt oberoende

Jag är lite osäker på ifall jag ställer upp ekvationssystemet rätt. Jag har ju tre vektorer men fyra koordinater. Jag tänker att om vi endast har den triviala lösningen så är vektorerna linjärt oberoende. Sedan undrar jag vilka sätt det finns för att bestämma vektor u4 som är ortogonal.
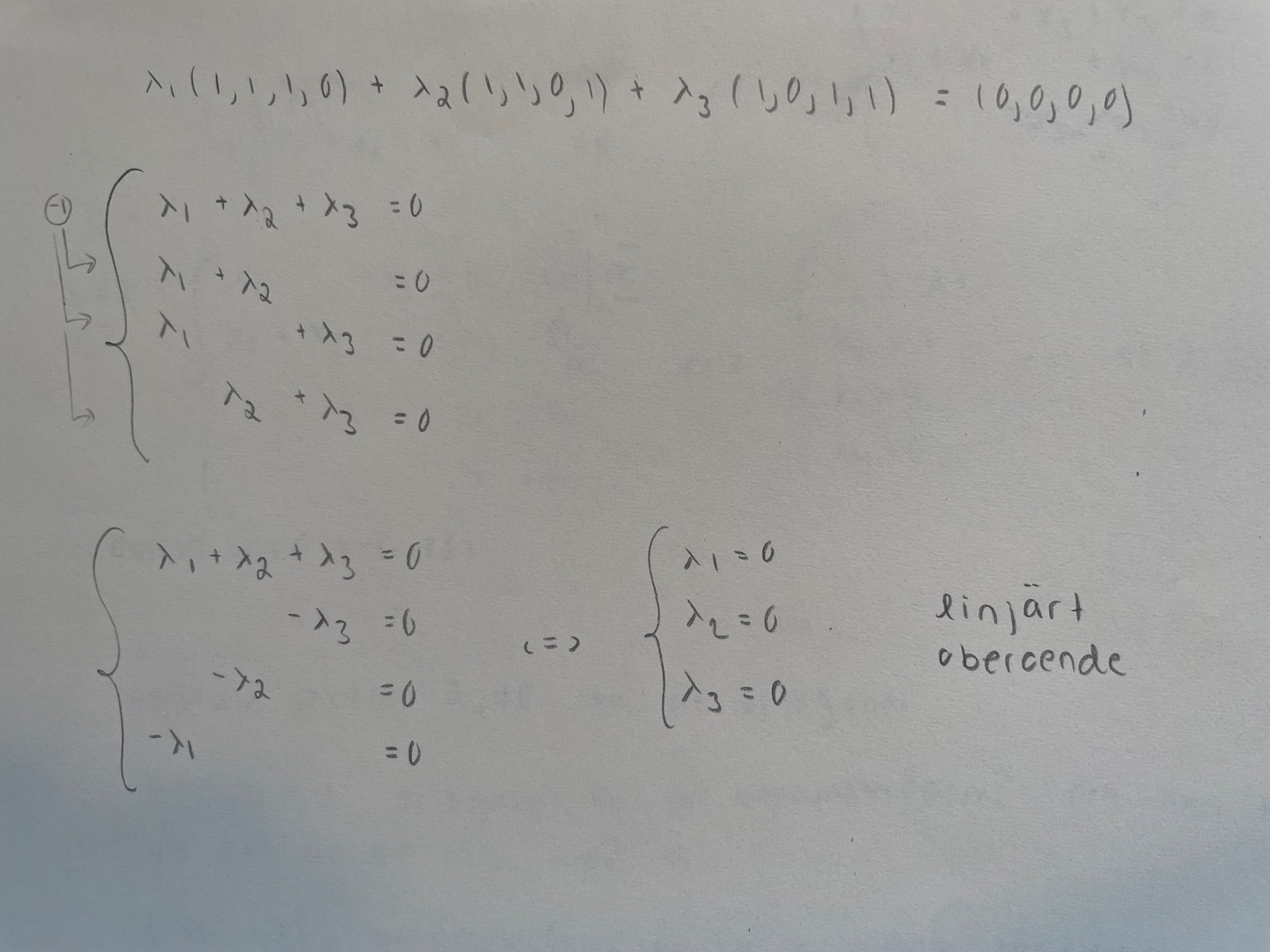
Jag vet att jag kan använda transponaten för att beräkna den fjärde vektorn men undrar om det finns någon mer metod
Jag tycker du borde kunna använda vilken linjärkombination som helst av dom tre vektorer som du har (om ingen koefficient är lika med noll).
Laguna skrev:Jag tycker du borde kunna använda vilken linjärkombination som helst av dom tre vektorer som du har (om ingen koefficient är lika med noll).
Hur menar du nu?
Jag löste den på följande vis för att ta reda på u_4: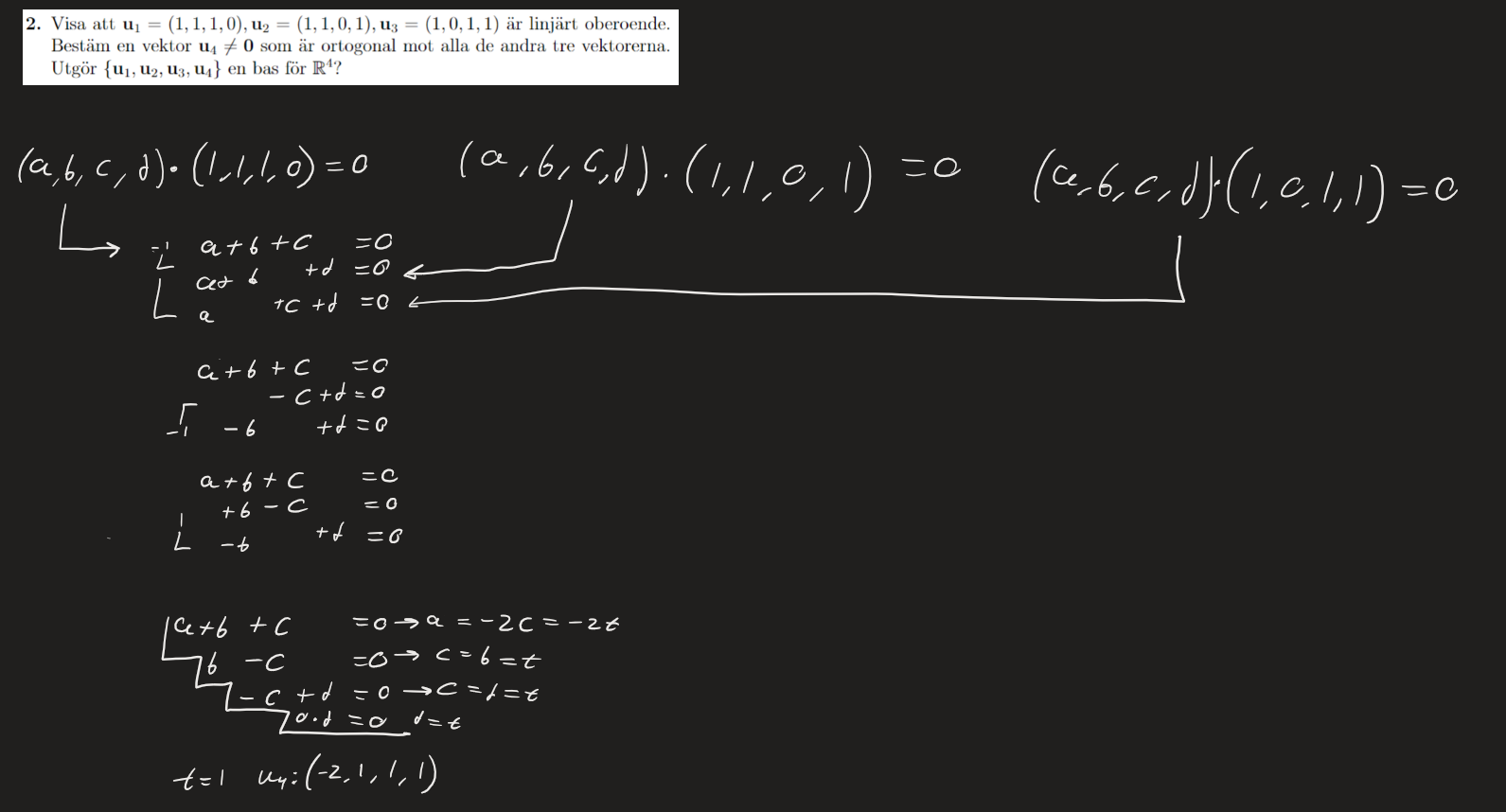
notsogenius skrev:Laguna skrev:Jag tycker du borde kunna använda vilken linjärkombination som helst av dom tre vektorer som du har (om ingen koefficient är lika med noll).
Hur menar du nu?
Jag tänkte att det bara gällde att hitta en ny vektor så att alla fyra var linjärt oberoende, men den skulle ju vara ortogonal också.
Etthejfrånpolhem skrev:Jag löste den på följande vis för att ta reda på u_4:
Om du lägger in dina basvektorer som kolonner i en matris så är din metod samma sak som att lösa det transponerade underbestämda ekvationssystemet
där är din vektor vektor
Och det i sin tur är samma sak som att bestämma nollrummet till matrisen , dvs (vilket i sin tur är ekvivalent med att bestämma det ortogonala komplementet till värderummet av dvs ).
Man kan även generalisera kryssprodukten till fyra dimensioner.
.