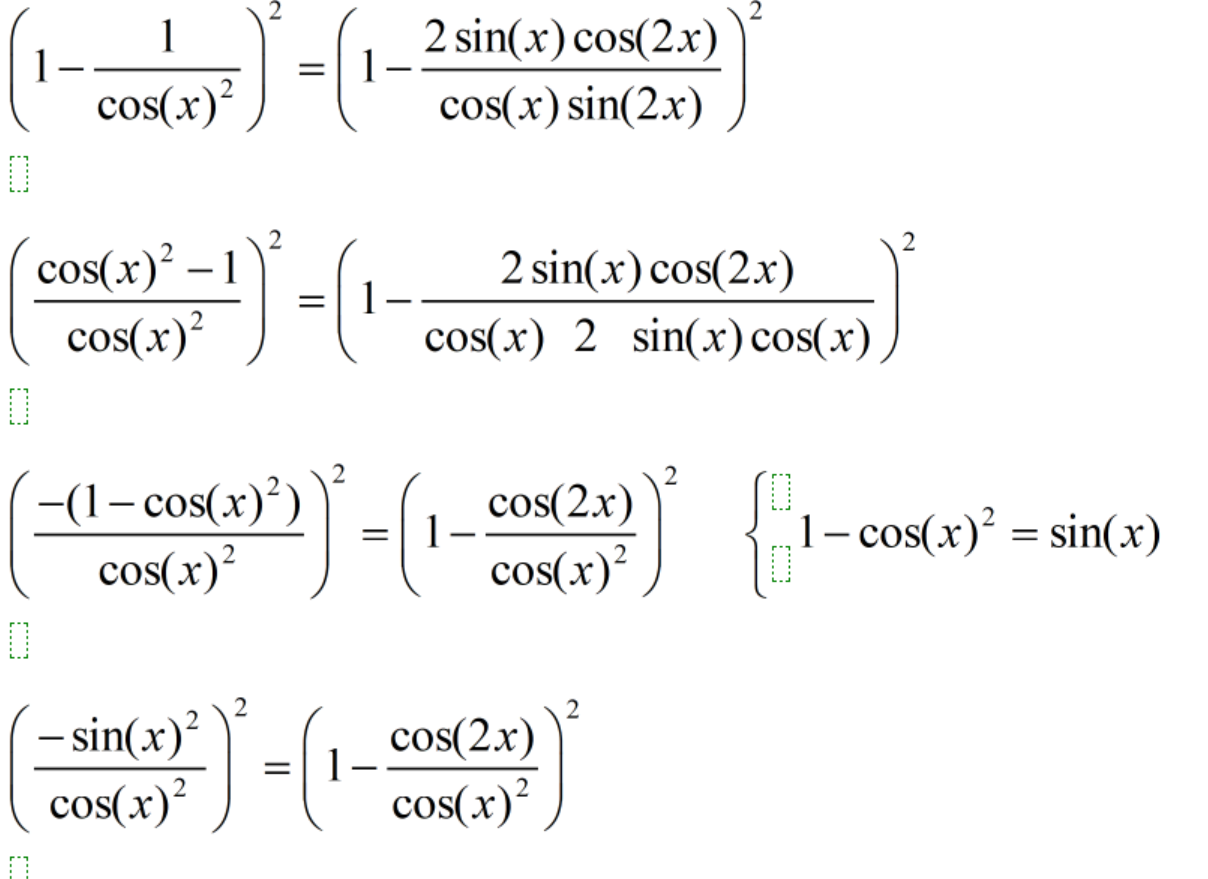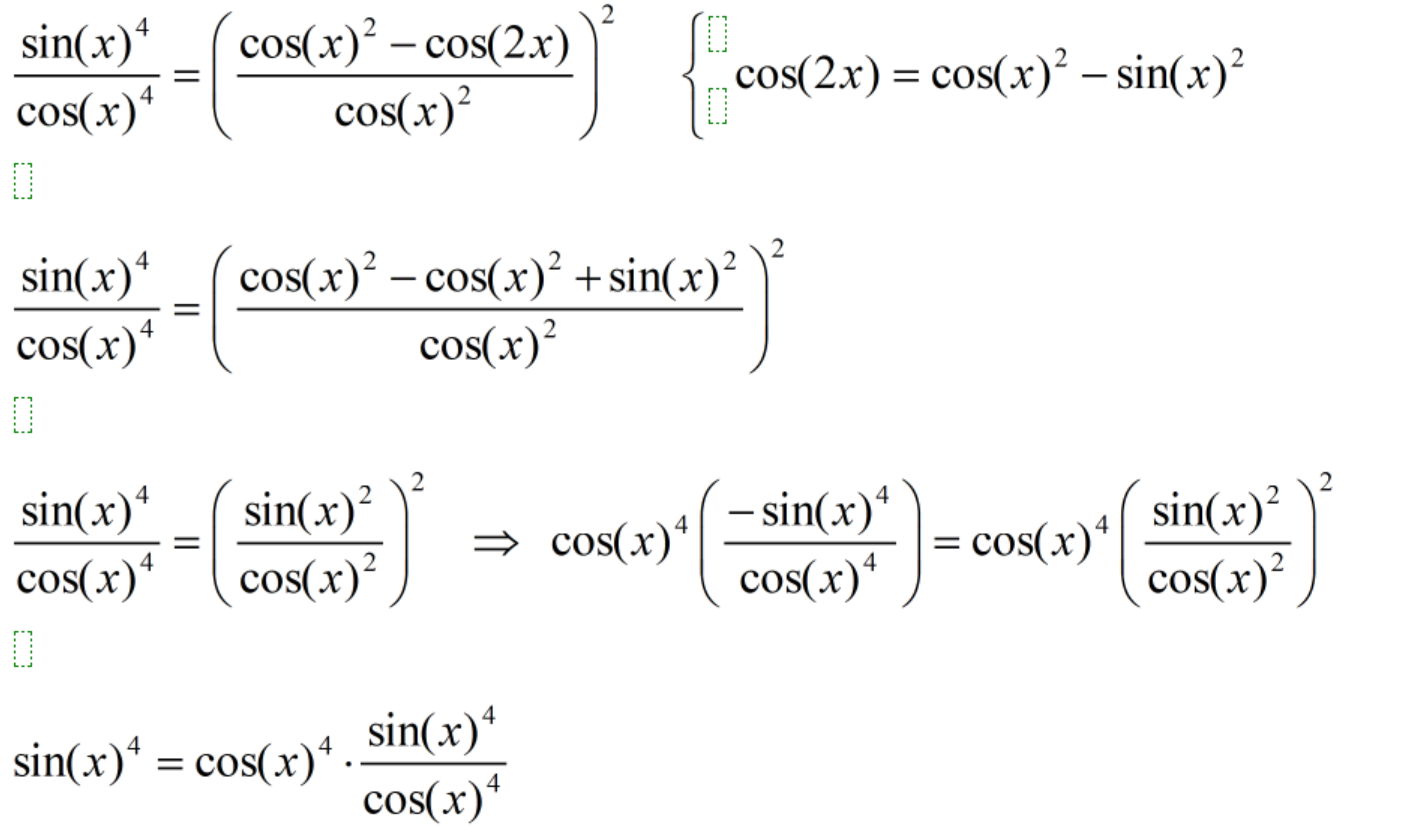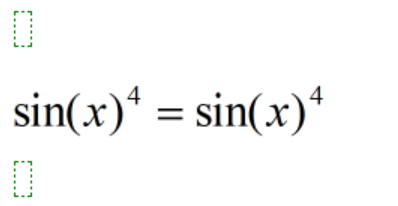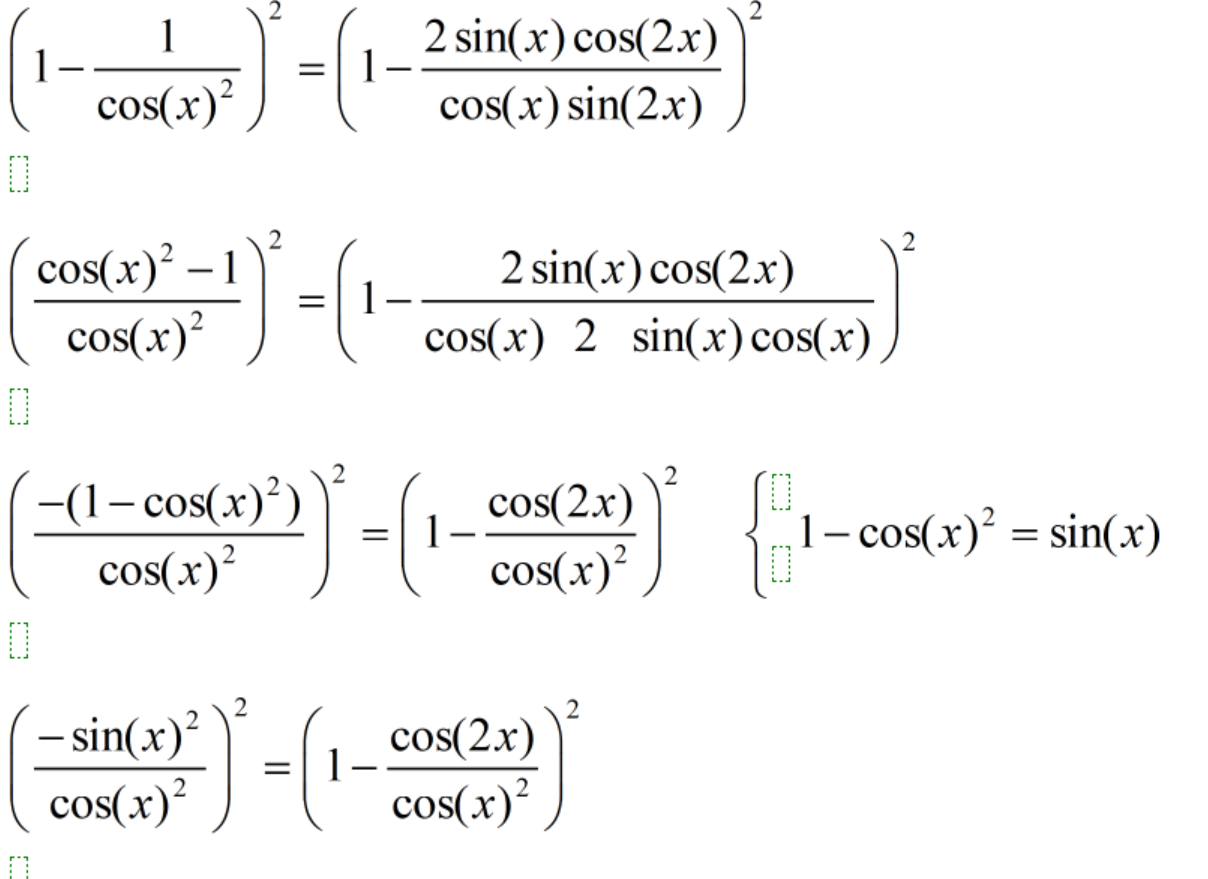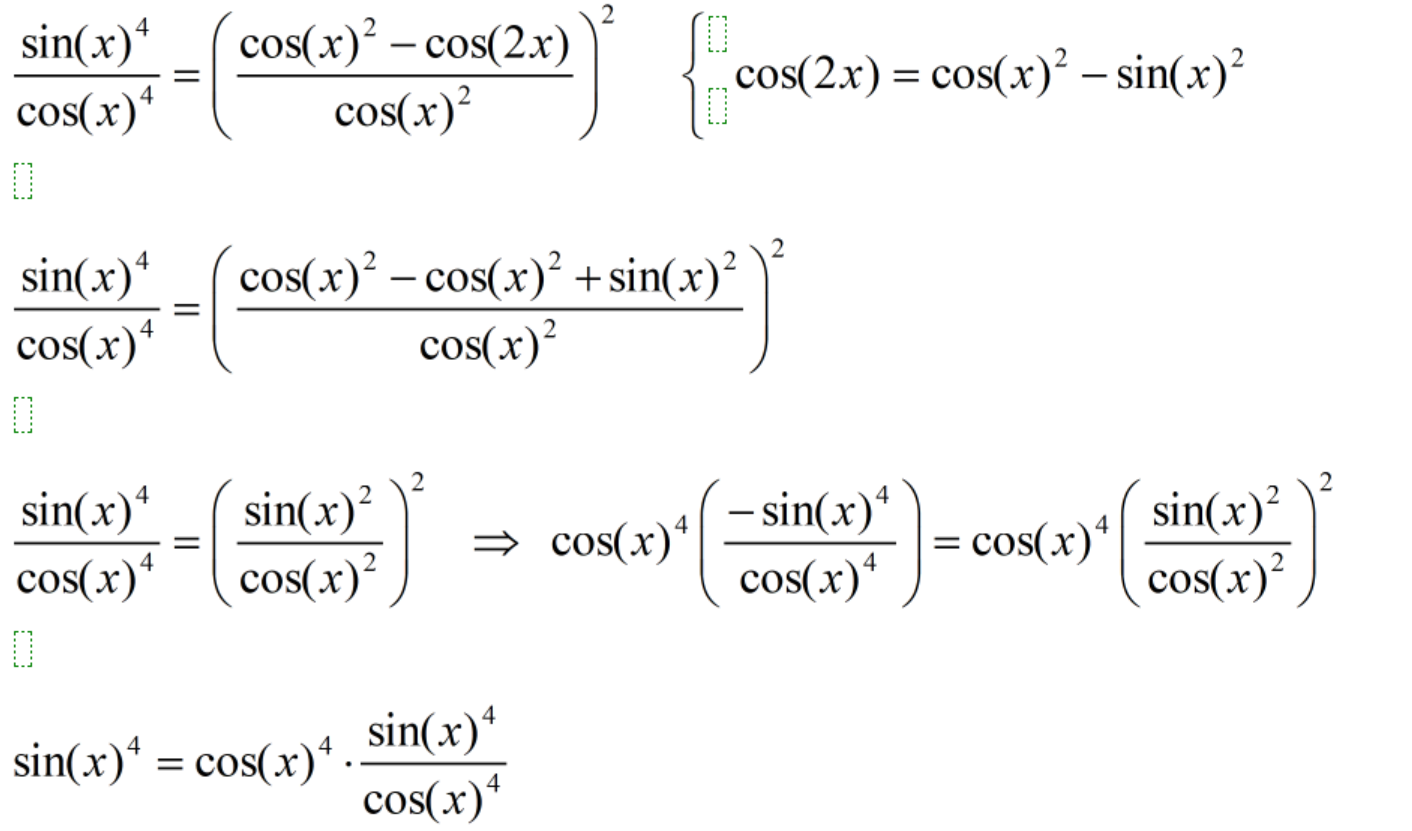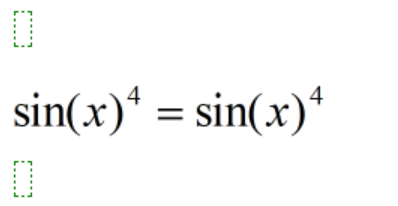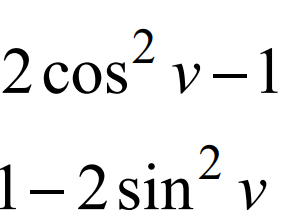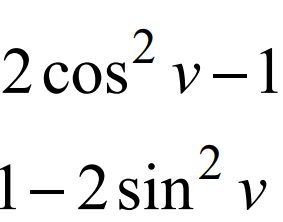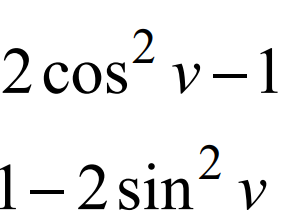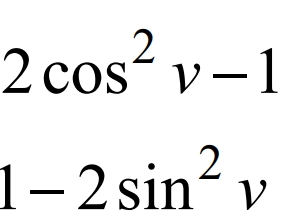"visa att" uppgift A-nivå
Hej!
Undrar om jag löst uppgiften rätt? Om något är fel vill jag gärna veta vad och varför. Undrar också hur bra min lösning är och om jag kan förbättra den på något sätt?


Jag läste ej till slutet, men du verkar kunna din algebra, men jag hade stannat vid 4:e ledet och valt denna väg
(1-1/cos^2(x))^2 = (1-cos(2x)/cos^2(x))^2
(-sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
(sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
Klart.
Tack för svaret!
Men jag undrar hur du fick det till (-sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
Är det så att du omvandlade i HL cos2x till cos^2x - sin^2x (formeln för dubbla vinkeln)... men då borde det stå (-sin^2(x)/cos^2(x))^2
och hur fick du VL till (-sin^2(x)/cos^2(x))^2
Det går att förenkla tills det bara står sin(x)4 = sin(x)4
Jag kan posta vad jag gjorde :D
Skulle vara tacksam om ni läste mitt svar till slutet och kommenterade på det!
itsLukas skrev:Det går att förenkla tills det bara står sin(x)4 = sin(x)4
Jag kan posta vad jag gjorde :D
Det skulle vara verkligen till hjälp om du postade, tack!
Trinity2 skrev:Jag läste ej till slutet, men du verkar kunna din algebra, men jag hade stannat vid 4:e ledet och valt denna väg
(1-1/cos^2(x))^2 = (1-cos(2x)/cos^2(x))^2
(-sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
(sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
Klart.
Tack för svaret!
Men jag undrar hur du fick det till (-sin^2(x)/cos^2(x))^2 = (sin^2(x)/cos^2(x))^2
Är det så att du omvandlade i HL cos2x till cos^2x - sin^2x (formeln för dubbla vinkeln)... men då borde det stå (-sin^2(x)/cos^2(x))^2
och hur fick du VL till (-sin^2(x)/cos^2(x))^2
itsLukas skrev:Det går att förenkla tills det bara står sin(x)4 = sin(x)4
Här kommer lösningen.
Sorry för det tog tid! Jag skrev den på dator så det är enkelt att läsa. (Jag har dålig handstill, men math type har inte det :). )
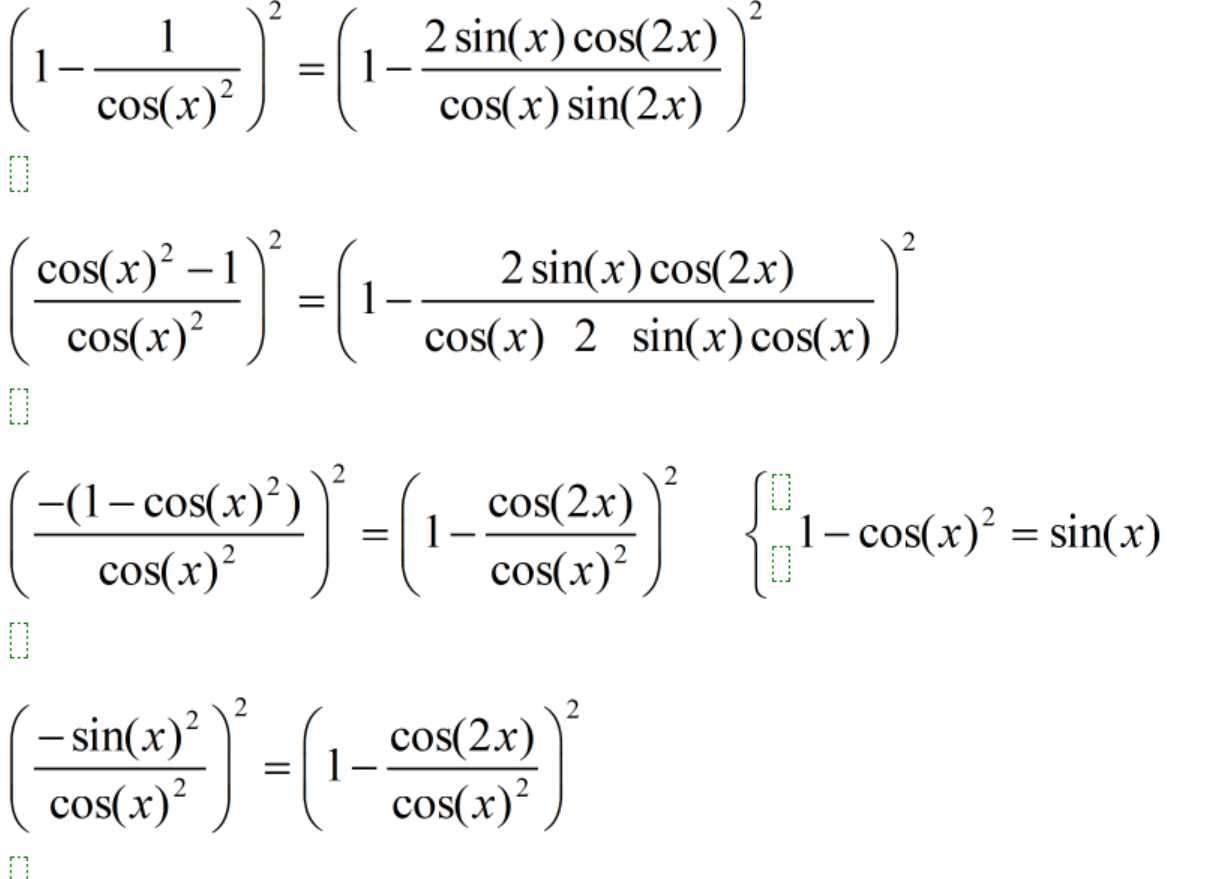
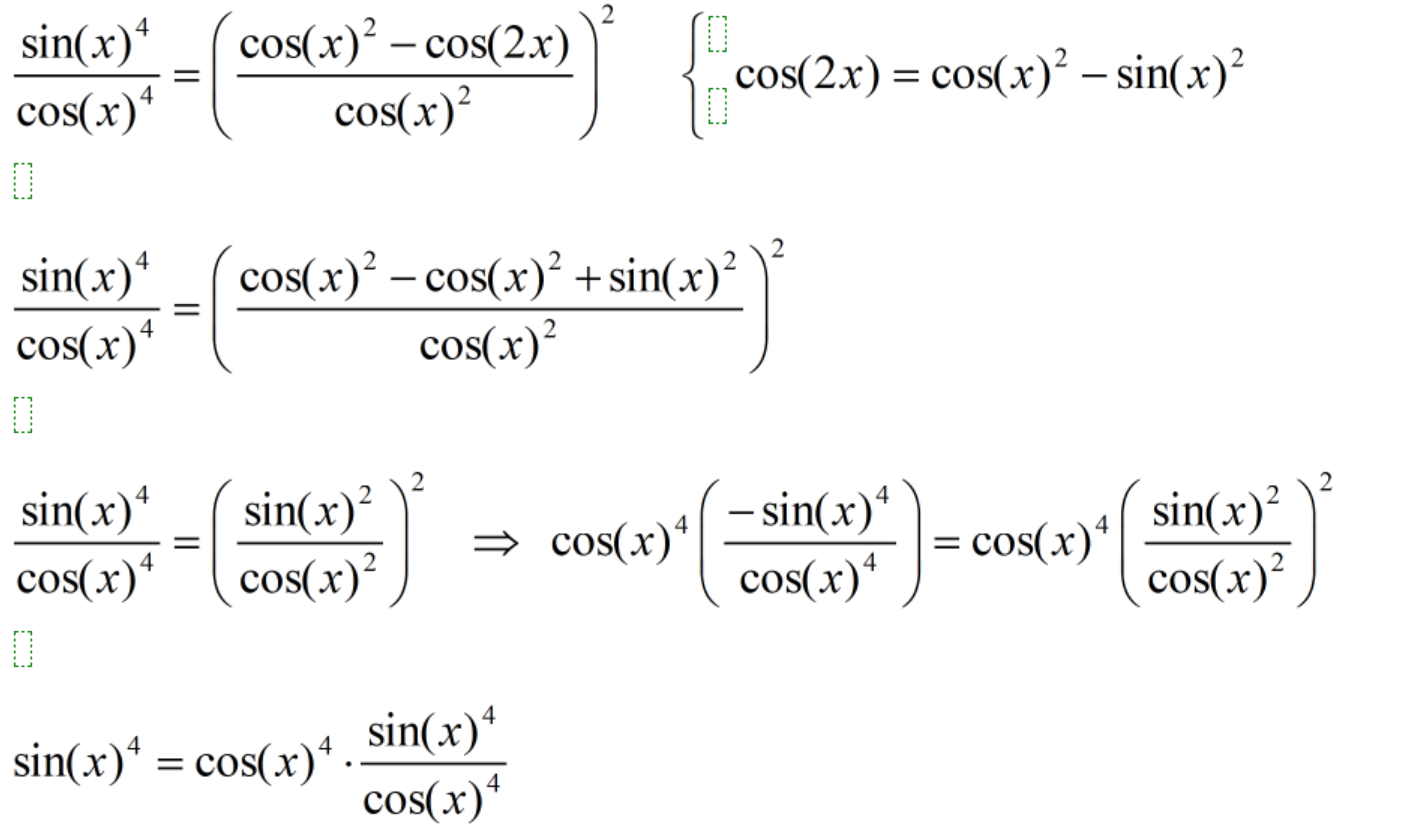
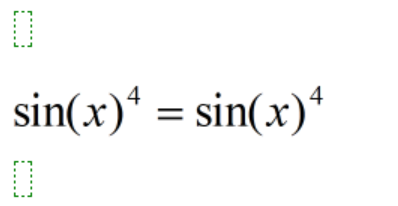
Detta tycker jag är det mest enklaste from. VL = HL
Logiskt är detta sant men till vad mer man vill göra kan jag inte säga :)
Hodlys skrev:Skulle vara tacksam om ni läste mitt svar till slutet och kommenterade på det!
Jag har läst till slutet och har tre kommentarer.
- Du bör inleda med att förutsätta att sin(2x) är skilt från 0. Annars är både vänster- och högerledet odefinierade.
- Du bör omvandla vänster-och högerled var för sig och inte fortsätta att ha det som en likhet mellan vänster- och högerled.
- Du kan stanna vid det gulmarkerade i bilden, eftersom vänster- och högerled här är identiska. Fortsättningen är onödig.


https://mathb.in/78486
itsLukas skrev:itsLukas skrev:Det går att förenkla tills det bara står sin(x)4 = sin(x)4
Här kommer lösningen.
Sorry för det tog tid! Jag skrev den på dator så det är enkelt att läsa. (Jag har dålig handstill, men math type har inte det :). )
Detta tycker jag är det mest enklaste from. VL = HL
Logiskt är detta sant men till vad mer man vill göra kan jag inte säga :)
haha inget att be om ursäkt för! Tack för svaret! Jag gjorde uppgiften återigen och kom fram till att man även kan skriva tan^4x=tan^4x (hoppas jag har rätt nu, lol)
Yngve skrev:Hodlys skrev:Skulle vara tacksam om ni läste mitt svar till slutet och kommenterade på det!
Jag har läst till slutet och har tre kommentarer.
- Du bör inleda med att förutsätta att sin(2x) är skilt från 0. Annars är både vänster- och högerledet odefinierade.
- Du bör omvandla vänster-och högerled var för sig och inte fortsätta att ha det som en likhet mellan vänster- och högerled.
- Du kan stanna vid det gulmarkerade i bilden, eftersom vänster- och högerled här är identiska. Fortsättningen är onödig.
Tack så jättemycket för svaret! Uppskattar det verkligen!
så även om VL har -1 och HL +1 så är de identiska på grund av att -1 spelar ingen roll tack vare att uttrycket är upphöjt med två, har jag rätt?
Trinity2 skrev:
https://mathb.in/78486
Tack så jättemycket för hjälpen! Uppskattar det verkligen! Omvandlingen av tan2x har jag inte tagit...men tack ändå!
Jag har dock en fråga, ni alla omvandlade cos2u= cos^2x - sin^2x
kan man lösa uppgiften genom att omvandla cos2u till de andra 2 omvandlingarna, liksom:
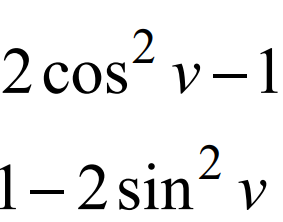
Hodlys skrev:itsLukas skrev:itsLukas skrev:Det går att förenkla tills det bara står sin(x)4 = sin(x)4
Här kommer lösningen.
Sorry för det tog tid! Jag skrev den på dator så det är enkelt att läsa. (Jag har dålig handstill, men math type har inte det :). )
Detta tycker jag är det mest enklaste from. VL = HL
Logiskt är detta sant men till vad mer man vill göra kan jag inte säga :)
haha inget att be om ursäkt för! Tack för svaret! Jag gjorde uppgiften återigen och kom fram till att man även kan skriva tan^4x=tan^4x (hoppas jag har rätt nu, lol)
Helt rätt, Jag testade också att får det till tan(x)4 Detta är bra !
Det verkar lite mer lättare att lösa till tan tycker jag :).
Hodlys skrev:Jag har dock en fråga, ni alla omvandlade cos2u= cos^2x - sin^2x
kan man lösa uppgiften genom att omvandla cos2u till de andra 2 omvandlingarna, liksom:
Jag menar, jag använde 2cos^2 x-1 i mitt första svar, dock vet jag inte om jag fick rätt...
Hodlys skrev:Hodlys skrev:Jag har dock en fråga, ni alla omvandlade cos2u= cos^2x - sin^2x
kan man lösa uppgiften genom att omvandla cos2u till de andra 2 omvandlingarna, liksom:
Jag menar, jag använde 2cos^2 x-1 i mitt första svar, dock vet jag inte om jag fick rätt...
menar du led 5 i din uträkning?
itsLukas skrev:Hodlys skrev:Hodlys skrev:Jag har dock en fråga, ni alla omvandlade cos2u= cos^2x - sin^2x
kan man lösa uppgiften genom att omvandla cos2u till de andra 2 omvandlingarna, liksom:
Jag menar, jag använde 2cos^2 x-1 i mitt första svar, dock vet jag inte om jag fick rätt...
menar du led 5 i din uträkning?
Ja, eller led 6, beror på hur man räknar
Hodlys skrev:itsLukas skrev:Hodlys skrev:Hodlys skrev:Jag har dock en fråga, ni alla omvandlade cos2u= cos^2x - sin^2x
kan man lösa uppgiften genom att omvandla cos2u till de andra 2 omvandlingarna, liksom:
Jag menar, jag använde 2cos^2 x-1 i mitt första svar, dock vet jag inte om jag fick rätt...
menar du led 5 i din uträkning?
Ja, eller led 6, beror på hur man räknar
Jag vågar inte att säga direkt av. Men.... Vid led 6 på HL där du har -cos(x)2 + 1 vilket också är sin(x)2
alltså -cos(x)2 + 1 = sin(x)2 Vilket tillslut kommer bli tan(x)4
Använda det uttrycket går men du valde inte den vägen. Jag tror det blev förmodligen fel runt led 7.
Hodlys skrev:[...] så även om VL har -1 och HL +1 så är de identiska på grund av att -1 spelar ingen roll tack vare att uttrycket är upphöjt med två, har jag rätt?
Det stämmer.
Generellt gäller att (a-b)2 = (b-a)2.
Detta eftersom (a-b) = (-1)*(b-a) och (c*d)2 = c2*d2, vilket ger oss att ((-1)*(b-a))2 = (-1)2*(b-a)2 = (b-a)2
Oj, vad lång din lösning blev! Jag håller med Yngves inlägg, men skulle gjort så här: