Visa att Tan (-v) = tan(180°-v)

Är följande "att visa"?

Nej, du skriver att tan(180°-v) = sin(180°-v) och att tan(180°-v) = cos(180°-v).

Inget av detta stämmer.

=======

Försök istället att utnyttja att tangens har en periodicitet på 180°, vilket betyder att sambandet tan(u) = tan(u+180°) gäller för alla vinklar u.

Nej, men du är ändå en bit på vägen.

tan(180-v)=sin(180-v)/cos(180-v)=sin(v)/-cos(v)=-sin(v)/cos(v)=sin(-v)/cos(v)=…

Ser du sista steget själv?

Nej, jag ser det inte, men jag vet att det är tan(-v). Eller, ja använda sig utav hur cos och sin beter sig i olika kvadranter och använda sig av definitionen av tangens så har man visat det. Okej. Tack.

Jag undrar också varför höjden på en triangel som har ena kateten på cirkelns rand är lika med värdet för tangens? Har inget med den här frågan att göra men 

Din andra fråga,

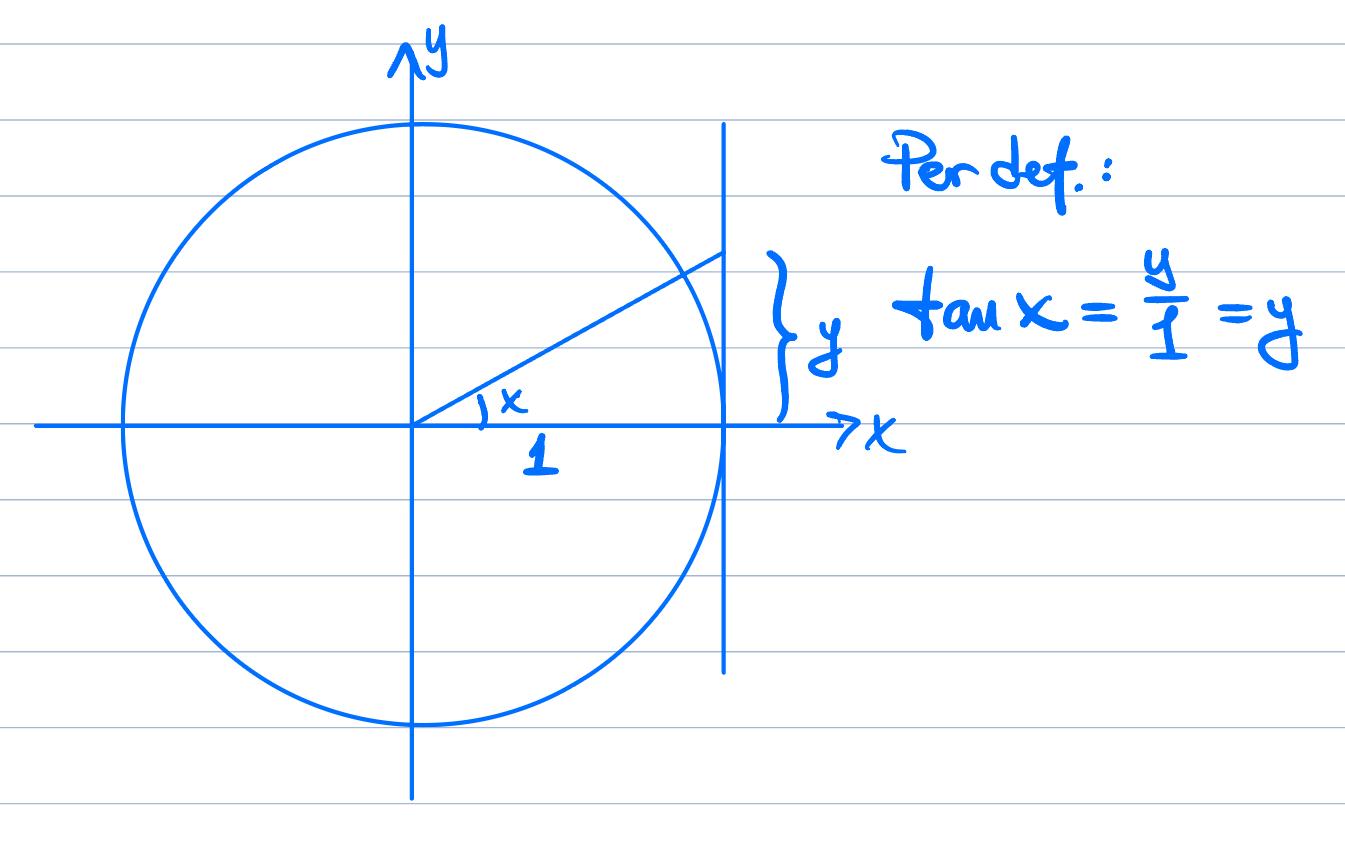
Jo..

Men, hur förstår jag att det värdet (y)då är lika med kvoten mellan sin/cos för R=1? Det är logiskt antar jag men jag kan inte koppla ihop det.

Hypotenusan i den rätvinkliga triangeln OAB har längden $\sqrt{1^2+y^2}=\sqrt{y^2+1}$

Det ger oss att $\sin(x)=\frac{y}{\sqrt{y^2+1}}$ och att $\cos(x)=\frac{1}{\sqrt{y^2+1}}$

Eftersom $\tan(x)=\frac{sin(x)}{cos(x)}$ så får vi att $\tan{x}=\frac{\frac{y}{\sqrt{y^2+1}}}{\frac{1}{\sqrt{y^2+1}}}=\frac{y}{1}=y$

Blev det tydligare då? 

Nej, jag vet inte.

Det är säkert exakt det du skriver men det är en viss skillnad och då går det inte.

Jag menar såhär:

Borde inte ditt x och y byta plats?

Och vad är det du undrar över?

Dom var inte relevanta till frågan så jag satte bara dit två godtyckliga variabler.. men vi använder ju oss av enhetscirkeln och då kan kan försöka representera den ordentligt naturligtvis.

Jag undrar varför höjden på kateten på som är tangent till cirkelns rand på den stora triangeln överensstämmer med kvoten mellan SIN(V) OCH COS (V) för den lilla triangeln DVS y/x (nu kastade jag om dom korrekt).

Är det något/några av följande påståenden du inte är med på?

1. Triangeln OAB är rätvinklig
2. Den till vinkeln $v$ motstående kateten har längden $H$
3. Den till vinkeln $v$ närliggande kateten har längden $1$
4. $\tan(v)=\frac{H}{1}=H$
5. $\tan(v)=\frac{\sin(v)}{\cos(v)}$
6. Alltså är $H=\frac{\sin(v)}{\cos(v)}$

======

Du kan även använda att den lilla och den stora triangeln är likformiga, vilket ger dig sambandet $\frac{y}{x}=\frac{H}{1}$, dvs $H=\frac{y}{x}$.

Detta tillsammans med $\sin(v)=y$ och $\cos(v)=x$ ger dig det samband du undrar över.

Yngve skrev:

Är det något/några av följande påståenden du inte är med på?

1. Triangeln OAB är rätvinklig
2. Den till vinkeln $v$ motstående kateten har längden $H$
3. Den till vinkeln $v$ närliggande kateten har längden $1$
4. $\tan(v)=\frac{H}{1}=H$
5. $\tan(v)=\frac{\sin(v)}{\cos(v)}$
6. Alltså är $H=\frac{\sin(v)}{\cos(v)}$

======

Du kan även använda att den lilla och den stora triangeln är likformiga, vilket ger dig sambandet $\frac{y}{x}=\frac{H}{1}$, dvs $H=\frac{y}{x}$.

Detta tillsammans med $\sin(v)=y$ och $\cos(v)=x$ ger dig det samband du undrar över.

Tack.

Jag förstår.