Visa att summan är 180 grader

Jag har bara tänkt att man kan använda radierna, men kommer verkligen inte på hur.
Tack i förhand!
Använd randvinkelsatsen på de båda vinklarna.
Tips om du inte kommer framåt
Gör på liknande sätt som i denna uppgift, med skillnaden att medelpunktsvinklarna inte nödvändigtvis är 180°. Kalla den ena medelpunktsvinkeln för x. Då blir den andra medelpunktsvinkeln 360° - x.
Använd sedan randvinkelsatsen för att uttrycka u och v i termer av x.
Yngve skrev:Använd randvinkelsatsen på de båda vinklarna.
Tips om du inte kommer framåt
Gör på liknande sätt som i denna uppgift, med skillnaden att medelpunktsvinklarna inte nödvändigtvis är 180°. Kalla den ena medelpunktsvinkeln för x. Då blir den andra medelpunktsvinkeln 360° - x.
Använd sedan randvinkelsatsen för att uttrycka u och v i termer av x.
Börjat såhär:

Jag kan väll inte uttrycka v med?
Bra början.
u = x/2
v = (360-x)/2
Kommer du vidare då?
Yngve skrev:Bra början.
u = x/2
v = (360-x)/2
Kommer du vidare då?
vänta, hur kan man göra så med v? det buktar ju utåt?
Ja randvinkelsatsen gäller även om mittpunktsvinkeln är större än 180°.
Yngve skrev:Ja randvinkelsatsen gäller även om mittpunktsvinkeln är större än 180°.
aha, är det samma sätt att bevisa det som när det är mindre än 180 grader?
Jag förstår inte vad du menar med "när det är mindre än 180 grader".
Vad är det som är mindre än 180 grader och vad är det som då ska bevisas?
Yngve skrev:Jag förstår inte vad du menar med "när det är mindre än 180 grader".
Vad är det som är mindre än 180 grader och vad är det som då ska bevisas?
jag menade hur randvinkelsatsen kan fungera på figuren längst till höger i bilden nedan. Är det samma bevis som för den längst till vänster (den jag är van att använda randvinkelsatsen för)?
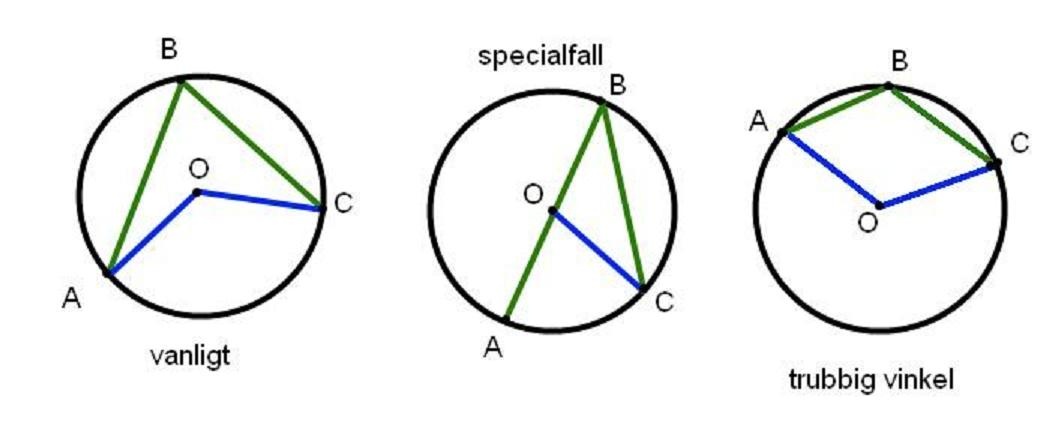
Du skriver "bevis", vilket förvirrar mig.
Du ska väl inte bevisa att randvinkelsatsen gäller?
-------
Om du istället menar om och hur randvinkelsatsen fungerar så är svaret att den fungerar även då randvinkeln är trubbig, dvs då medelpunktsvinkeln är större än 180° och att den fungerar på samma sätt som då randvinkeln är spetsig eller rät.

Rita in de två sträckor som behövs för att det skall bildas två medelpunktsvinklar som står på samma vinkelbågar som u respektive v.
Enligt randvinkelsatsen är medelpunktsvinklarna 2u respektive 2v. Vi kan se att 2u+2v=...
Yngve skrev:Du skriver "bevis", vilket förvirrar mig.
Du ska väl inte bevisa att randvinkelsatsen gäller?
-------
Om du istället menar om och hur randvinkelsatsen fungerar så är svaret att den fungerar även då randvinkeln är trubbig, dvs då medelpunktsvinkeln är större än 180° och att den fungerar på samma sätt som då randvinkeln är spetsig eller rät.
jag menar hur man kan visa att randvinkelsatsen fungerar för trubbig vinkel också?
Smaragdalena skrev:Rita in de två sträckor som behövs för att det skall bildas två medelpunktsvinklar som står på samma vinkelbågar som u respektive v.
Enligt randvinkelsatsen är medelpunktsvinklarna 2u respektive 2v. Vi kan se att 2u+2v=...
aa det fungerade men förstår bara inte riktigt varför randvinkelsatsen funkar på trubbig vinkel
Kolla sista stycket i det här avsnittet.
Yngve skrev:Kolla sista stycket i det här avsnittet.
men det är ju för spetsig vinkel?
Dela in fyrhörningen i två likbenta trianglar. Titta på vinkelsumman i fyrhörningen.

Dr. G skrev:Dela in fyrhörningen i två likbenta trianglar. Titta på vinkelsumman i fyrhörningen.
vet att det blir 180 grader men förstår inte varför randvinkelsatsen gäller för trubbig vinkel?
lovisla03 skrev:Yngve skrev:Kolla sista stycket i det här avsnittet.
men det är ju för spetsig vinkel?
Vinkeln på deras bild är spetsig, men det är bara en illustration för att göra tydligt vilka vinklar de pratar om. Det antas ingenstans i beviset att vinkeln måste vara spetsig. Om du vill så kan du rita en egen figur med trubbig vinkel istället och göra om beviset precis likadant utifrån din illustration.
Russell skrev:lovisla03 skrev:Yngve skrev:Kolla sista stycket i det här avsnittet.
men det är ju för spetsig vinkel?
Vinkeln på deras bild är spetsig, men det är bara en illustration för att göra tydligt vilka vinklar de pratar om. Det antas ingenstans i beviset att vinkeln måste vara spetsig. Om du vill så kan du rita en egen figur med trubbig vinkel istället och göra om beviset precis likadant utifrån din illustration.
ok! tack!





