Visa att sambandet stämmer
Hej,
Jag har dessvärre fastnat på en uppgift... där jag ska försöka visa hur dessa tre ledtrådar stämmer överens med integralen. 
Har svårt att hitta vart jag ska börja och hur jag ska hitta f(x), om jag ska kunna gör det? Eftersom att f(x) inte är definierad i intervallet så är desmos inte heller till hjälp...
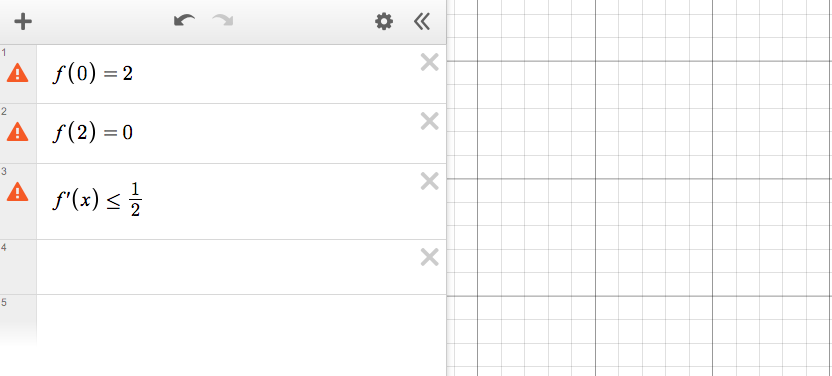
Tacksam för lite tydligare riktlinjer :)
Om man börjar i (0, 2) och sedan går uppåt så brant som den givna derivatan tillåter, hur ser kurvan ut då?
Så brant som den tillåter, alltså 1/2?
Eftersom att f'(x)<=1/2?
Sockerkakan 1 skrev:Så brant som den tillåter, alltså 1/2?
Ja. Låt alltså f(x) = x/2+2 i stort sett hela vägen fram till x = 2 och störtdyk sedan ner till (2,0).
På det sättet får du så stort värde på integralen som möjligt.
- Vilket värde är det?
Försök sedan med en liknande tankesätt definiera f(x) så att du får ett så litet värde på integralen som möjligt.
- Vilket värde är det?
Rita och visa eller beskriv med ord hur du tänker.
Typ något sånt? Eller är jag lite ute och cyklar nu...?
På rätt väg men på slutet ser det ut som derivata blir väldigt hög?
har du provat att störtdyker direkt efter 0 och sen ta dig upp till 0 med maximal tillåten hastighet?
Något i den här stilen? Eller har jag missuppfattat hur du menar? :)
Kan du få den negativa delen att bli större?
Om du kan få funktionens graf att ligga så högt ovanför x-axeln som möjligt så blir integralens värde så stort som möjligt.
Om du kan få funktionens graf att ligga så långt under x-axeln som möjligt så blir integralens värde så litet som möjligt.
Om f(x)=x/2+2 och sedan ritar upp det samt integrerar så får jag det största värdet till 5 vilket är vad som ingår i intervallet, stämmer detta då?
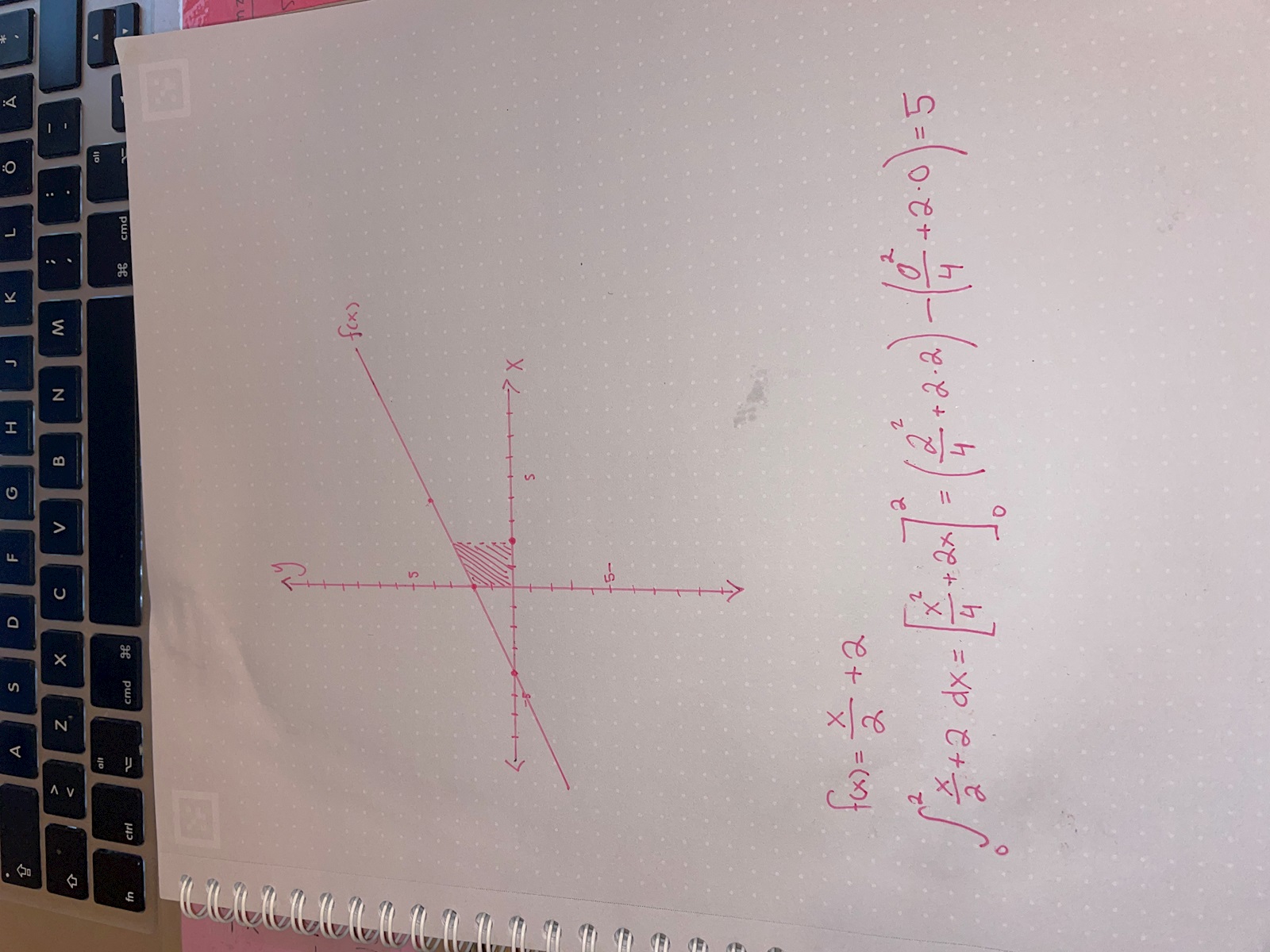
Då behöver jag alltså bara hitta en funktion vars minsta värde är -1 (då det ingår i det givna intervallet)? Men hur? Jag ska jag utgå från punkten (2,0) för att hitta funktionen?
Eller finns det bättre metoder?
Sockerkakan 1 skrev:Om f(x)=x/2+2 och sedan ritar upp det samt integrerar så får jag det största värdet till 5 vilket är vad som ingår i intervallet, stämmer detta då?
Ja, men eftersom f(2) = 0 så måste funktionen störtdyka ner mot 0 alldeles innan x når värdet 2.
Det betyder att det blir en yttepyttesmal strimma som inte ingår i området. Bidraget till integralen är nästan försumbart, men leder till att integralens värde definitivt är mindre än 5.
Då behöver jag alltså bara hitta en funktion vars minsta värde är -1 (då det ingår i det givna intervallet)? Men hur? Jag ska jag utgå från punkten (2,0) för att hitta funktionen?
I din första ansats när du sökte integralens maximala värde har du försökt få funktionsgrafen att ligga så högt ovanför x-axeln som möjligt, detta genom att utgå från den givna punkten (0, 2) och sedan följa den maximala lutningen 1/2 så långt du bara kan.
Nu, när du letar efter integralens minsta värde, så ska du tänka tvärtom. Du vill att grafen ska vara så långt under x-axeln som möjligt, med samma villkor som tidigare.
Pröva att tänka tvärtom och baklänges, dvs utgå från (2, 0) och rita grafen bakåt mot y-axeln med så brant lutning som möjligt så långt som möjligt. Men precis innan du når x = 0 så måste grafen göra ett jätteskönt upp till punkten (0, 2).
Tror fortfarande att det är något som jag missar... Chansade för att hitta det minsta värdet så att integralen stämmer överens om att det ska bli -1.
När jag försökte rita upp det lite så kom jag fram till dessa men det känns heller inte rätt.... förstår inte vad det är som jag missar....
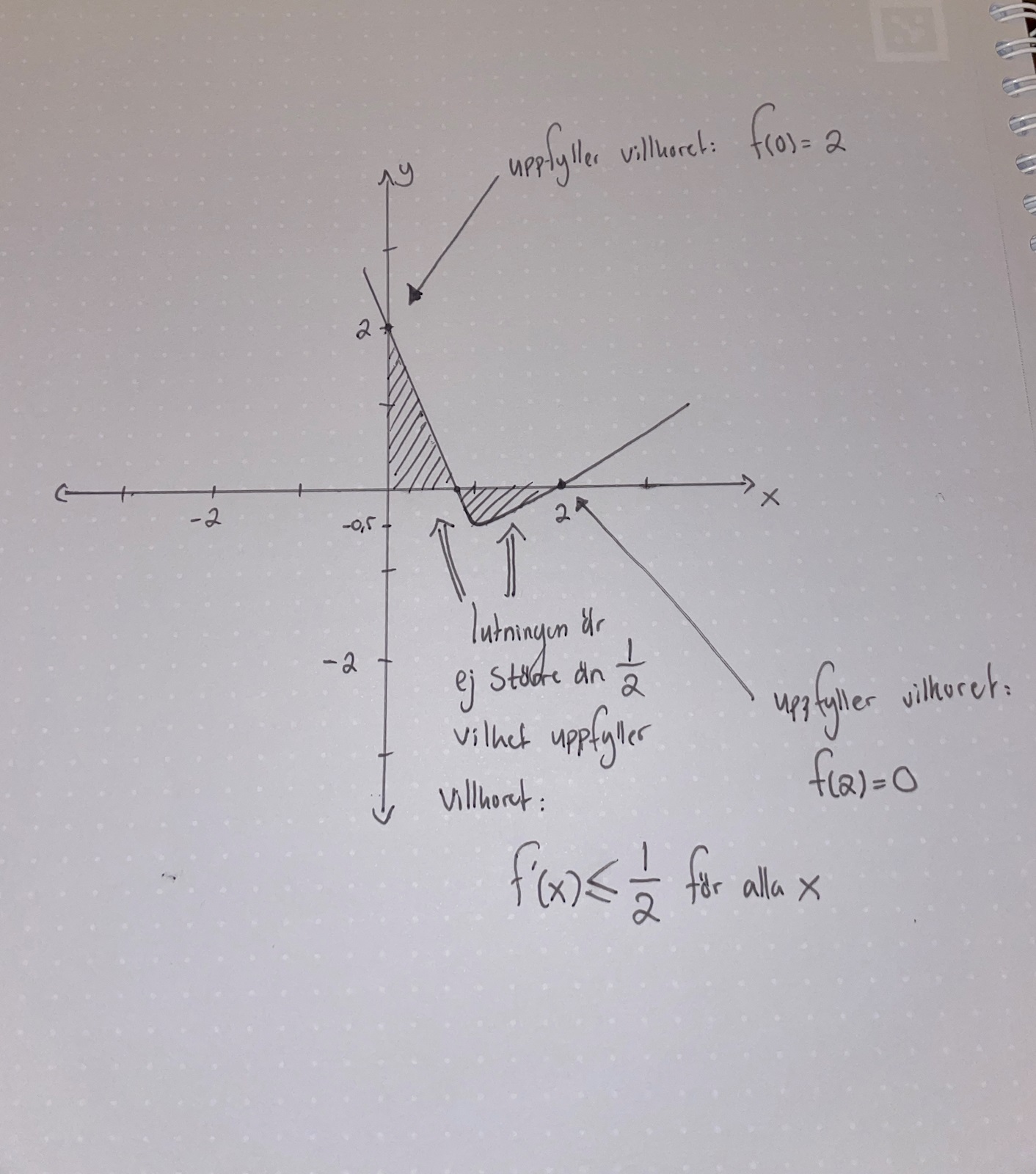
Kan du få minimum att ligga längre till vänster?
Låt grafen störtdyka från (0,2) så brant det bara går och så långt ner det bara går samtidigt som den därefter ska arbeta sig upp till (2,0) med en lutning som inte överskrider gränsen:
Men behöver jag inte veta själva lutningen för linjen som "störtdyker"?
Det gör väldigt liten skillnad om k-värdet är -100 eller -999 999 999 999. Räkna med en lodrät linje för enkelhets skull.
Lutningen är ju derivatan, ska jag bara tolka det som att lutningen kan vara oändligt negativt?
Så det finns inget direkt värde på derivatan/lutningen i detta fall?
Sockerkakan 1 skrev:Lutningen är ju derivatan, ska jag bara tolka det som att lutningen kan vara oändligt negativt?
Ja, lutningen är nästan minus oändligheten.
Det här är precis samma sak som du gjorde I det första fallet, när du ville ha så stort värde på integralen som möjligt.
Då såg din graf ut som det blåmarkerade i bilden: Den utgår från (0,2) och har sedan max positiv lutning 1/2 fram till precis innan x = 2, då den störtdyker ner mot slutpunkten (2,0):
