Visa att Pythagoras ekvation....
Visa att Pythagoras ekvation x2+y2= z2 har oändligt många jämna heltalslösningar, dvs. lösningar där x, y och z är är alla jämna tal
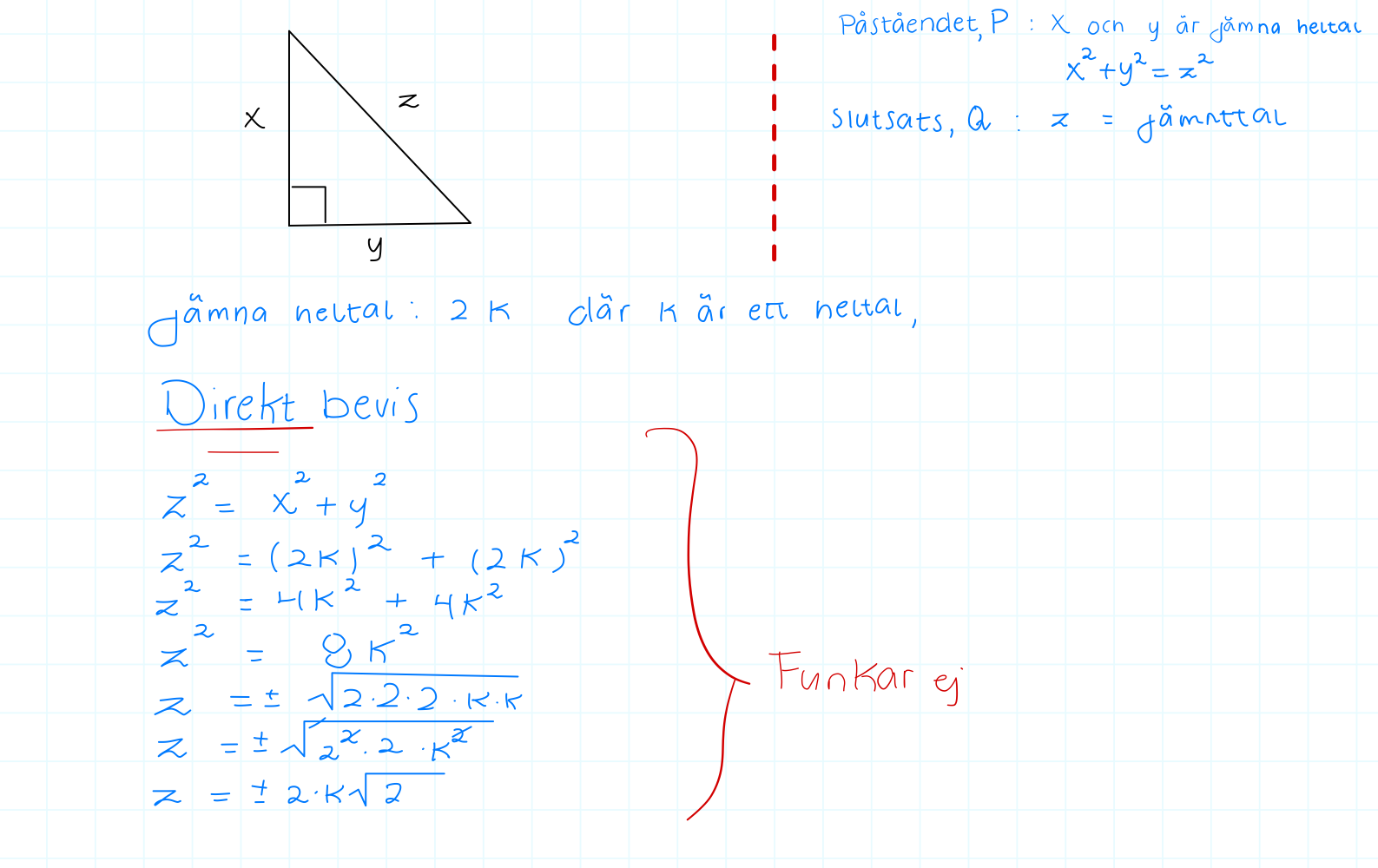
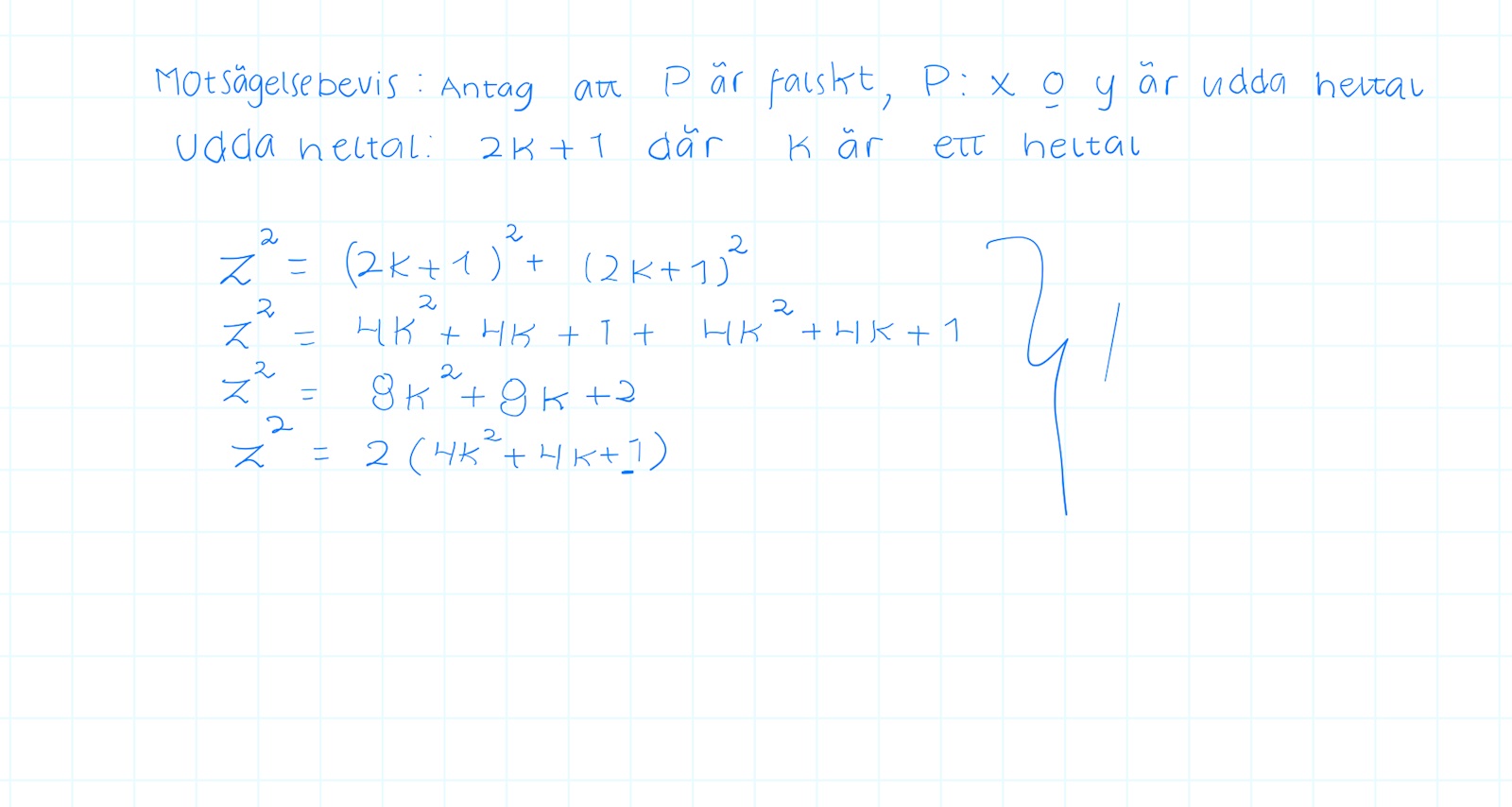
känner att jag har kört fast vet inte om jag riktigt förstod frågan ordenligt, hjälp?
Om du utgår från en lösning som du vet finns, exempelvis längderna 3, 4, 5 så kan man visa att 3k, 4k, 5k är lösningar till ekvationen där k är ett heltal.
men måste inte x och y vara positiva tal?
fysik3 skrev:men måste inte x och y vara positiva tal?
Jo, egentligen är det så. Men ekvationen x2+y2 = z2 gäller även för negativa värden på x, y och z.
Om vi vill förtydliga att det handlar om positiva lösningar så kan vi göra det enligt nedan.
Der vi hittills har missat är att vi enligt uppgiften ska visa att det gäller för oändligt många jämna tal.
Det kan vi uppnå om vi ändrar lite på det utmärkta förslaget från Eagle314.
Utgå från heltalslöningen 3, 4 och 5.
Om nu n är ett positivt heltal så är både 2n*3, 2n*4 och 2n*5 positiva jämna heltal som uppfyller Pythagoras sats.
Bra träning är att visa att detta faktiskt stämmer.
Det du gör fel i dina lösningar är att du antar att x=y, vilket inte behöver stämma (faktum är att det inte finns några sådana lösningar, vilket vi ser från ditt direkta bevis).
Yngve skrev:fysik3 skrev:men måste inte x och y vara positiva tal?
Jo, egentligen är det så. Men ekvationen x2+y2 = z2 gäller även för negativa värden på x, y och z.
Om vi vill förtydliga att det handlar om positiva lösningar så kan vi göra det enligt nedan.
Der vi hittills har missat är att vi enligt uppgiften ska visa att det gäller för oändligt många jämna tal.
Det kan vi uppnå om vi ändrar lite på det utmärkta förslaget från Eagle314.
Utgå från heltalslöningen 3, 4 och 5.
Om nu n är ett positivt heltal så är både 2n*3, 2n*4 och 2n*5 positiva jämna heltal som uppfyller Pythagoras sats.
Bra träning är att visa att detta faktiskt stämmer.
det jag menade var att x och y bör vara jämna heltal och om vi utgår från att x=3k och y=4k där k är ett heltal finns det risk för t.ex. att 3k inte är ett jämnt tal. och om vi nu utgår att x= 3k och y=4k där k är ett heltal ger pythagorssats att
z2 = (3k)2 + (4k)2
z2=25k2
z= 5k om k inte är ett jämnt tal kommer väl z jämn heltalslösning.
Låt k vara ett jämt heltal (dvs k=2p där p är ett heltal). Då blir både 3k och 4k jämna heltal för alla möjliga jämna värden på k.
fysik3 skrev:
det jag menade var att x och y bör vara jämna heltal och om vi utgår från att x=3k och y=4k där k är ett heltal finns det risk för t.ex. att 3k inte är ett jämnt tal. och om vi nu utgår att x= 3k och y=4k där k är ett heltal ger pythagorssats att
z2 = (3k)2 + (4k)2
z2=25k2
z= 5k om k inte är ett jämnt tal kommer väl z jämn heltalslösning.
Är du med på att om x är ett heltal och n är ett heltal så är 2n*x ett jämnt heltal?
Om ja, är du då även med på att både 2n*3, 2n*4 och 2n*5 är jämna heltal?
Om ja så räcker det att du visar att ekvationen (2n*3)2+(2n*4)2 = (2n*5)2 gäller för alla heltal n (positiva heltal n om du vill begränsa till enbart positiva jämna heltalslösningar).
okej jag hänger med men kan jag istället för att använda 3, och 4 ha k och m där k och m är heltal
x=2k
y=2m
x2+y2 = z2
(2k)2 + (2m)2 = z2
4k2m2= z2
z=2(km)
z= jämn heltal eftersom 2 gånger ett tal är alltid ett jämnt tal
fysik3 skrev:okej jag hänger med men kan jag istället för att använda 3, och 4 ha k och m där k och m är heltal
x=2k
y=2m
x2+y2 = z2
(2k)2 + (2m)2 = z2
4k2m2= z2
z=2(km)
z= jämn heltal eftersom 2 gånger ett tal är alltid ett jämnt tal
insåg lite sent att det var vad calle skrev men tack hörni!
fysik3 skrev:okej jag hänger med men kan jag istället för att använda 3, och 4 ha k och m där k och m är heltal
x=2k
y=2m
x2+y2 = z2
(2k)2 + (2m)2 = z2
4k2m2= z2
Det blir lite fel i sista steget här.
Vi får 4(k2+m2)=z2
.
För att z ska bli ett jämt positivt tal måste k och m vara sådana att roten ur summan av deras kvadrater blir ett heltal. För att detta ska gälla kan vi t.ex. säga att k=3 och m=4.



