Visa att polynomekvationen har en rot som är.. och lös ekv. fullständigt
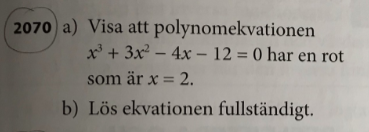

Detta är nog basic matte men jag undrar, nu när jag har fått ett noll ställe och enligt faktorsatsen har (x-2) som en faktor i polynomet. Gör en polynomdivision för att lösa ekvationen fullständigt får jag att x=2 , x=-2 , x-3.
Men vad är det jag har fått egentligen, det skär inte x-axeln, kallar man det nollställen eller hur funkar detta tänk.
Har någon tips på en bra förklaring på nätet eller en bok?
Den grafen stämmer inte:
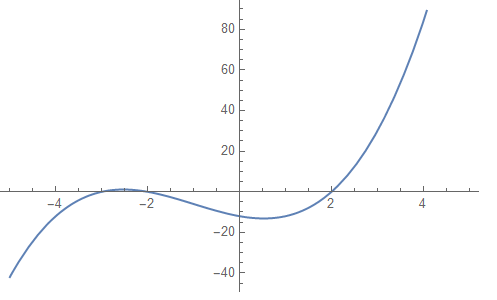
Så skumt vad har jag gjort för fel?
Herre min
Tack
Vet inte varför man blir så osäker på matte ibland!
Raif skrev:Men vad är det jag har fått egentligen, det skär inte x-axeln, kallar man det nollställen eller hur funkar detta tänk.
Bra fråga. Nu råkade du ju skriva fel i funktionsuttrycket, men tänk om vi istället hade haft ekvationen x3+x2-4x-24 = 0 med en rot x = 3, se bild.

Då skulle vi efter faktorisering få
(x-3)(x2+4x+8) = 0
De två övriga rötterna blir då x=-2+2i och x=-2-2i
Svaret på din fråga är ja, polynomet har fortfarande tre nollställen (varav två är komplexa).




