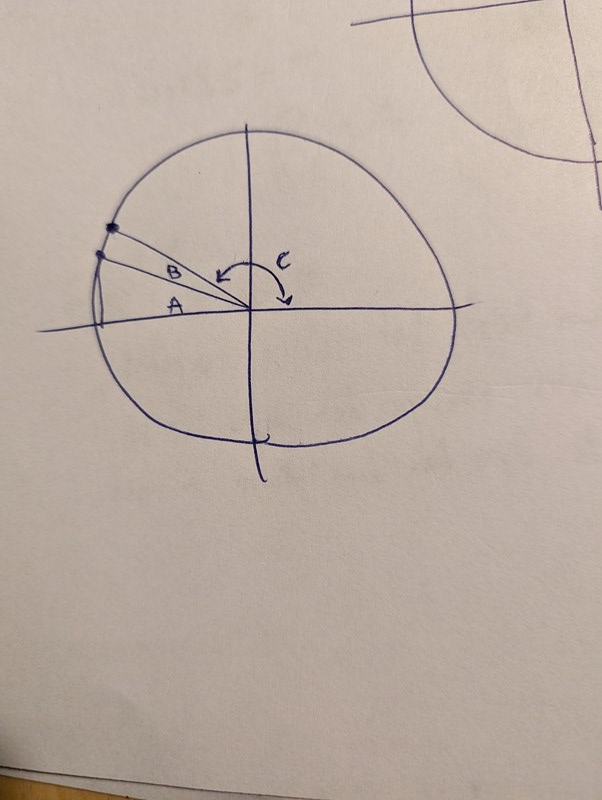Visa att h = uttryck.
Hej,
Behöver hjälp med fråga 4372.
Jag vet inte vad jag ska visa, jag har några täckta A4 med alla möjliga försök till lösningar. Jag vet inte. Har i slutändan inte kommit någonstans egentligen.

Hej.
Involverar någon av dina lösningar möjligen areasatsen?
Nej, den kändes irrelevant. Har mest försökt skriva om sinussatsen på olika sätt och uttryckt h utifrån de andra sidorna och försökt slänga runt allt så det ska se ut som svaret.
Försöker med den lite då..
Hej, förresten
Nej
Jag klarar av att skriva två uttryck för arean.
CbSIN (A) /2
Och
CaSIN(B) /2
Det är allt
Skilj gärna på små och stora bokstäver.
Det finns även Area = ab*sin(C) och Area = ch/2.
Jo, tänkte inte på det.
Jag kollade facit istället, är inte intelligent nog till att föra de logiska resonemang som krävs för att kunna härleda rätt lösning på uppgiften. Förstår knappt svaret. Kan inte sitta i flera timmar med en uppgift.
Tack för din tid.
Jag kan erkänna att jag inte omedelbart ser hur jag skulle göra, trots att jag är bra på det här. Tänka en bra stund kombinerat med lekande med areasats och sinussats skulle förmodligen leda till målet.
Det enda jag ser direkt som du kanske inte tänkte på är att A+B = 180o - C, så sin(A+B) = sin(C). Om det hjälper vet jag inte.
Nej, lite knivigt är det väl.
Det dryga är att jag försöker allt jag kan, vrider och vänder på alla satserna, bevisar dom. Försöker tänka nyanserat kring allt, och så vidare.
Jag skulle säga att jag överlag är duktig på att lära mig. Men jag lär mig inte, det händer ingenting i huvudet på mig när jag sitter och försöker. Det kopplar inte, jag får inget "ah, ja, just det". Man har ingen kontroll över sin egen förståelse egentligen, utan antingen begriper man eller så gör man inte det. Någonting som retar mig enormt.
Det du skriver står i facit... Men jag förstår inte. Och då förklarade du ett liknande problem för mig igår eller förrgår. Jag har ritat några enhetscirklar här med alla vinklar några gånger och försökt förstå att SIN(180-C) = SIN(A+B) = SIN(C), men jag gör det inte.
A+B+C = 180, för det är en triangel. Sen använder jag bara först att sin(180+x) = -sin(x) och sen sin(-x) = -sin(x).
Att sin(v) = sin(180°-v) framgår av enhetscirkeln.
Sin v = sin(180°-v) är superlogiskt och jag är med på det, men inte sin(A+B) = SIN(180-C) = SIN(C). Då är det två vinklar inblandade, som är olika dessutom. Beroende på vilket hörn jag då ska gå efter på vinkeln C så ger ju det helt olika värden.
Eftersom det är en triangel så gäller att A+B+C = 180°, dvs C = 180°-(A+B).
Med sin(C) = sin(180°-C) får vi alltså sin(C) = sin(180°-(180°-(A+B)) = sin(180°-180°+(A+B)) = sin(A+B)
Ja, men då är första bilden här en korrekt tolkning och den andra.. ja, trianglar i en cirkel typ ^^'