Visa att gränsvärde existerar mha epsilon delta definitionen

Hej, försöker visa att följande gränsvärde existerar i (x,y)=(0,0) genom att anta att funktionen närmar sig 1 då (x,y) närmar sig (0,0). Har fastnat vid $|x-3| \leq \epsilon$ , är ute efter att få uttrycket $\sqrt{x^2-y^2} < \epsilon*t$ för något värde t så jag kan sätta $\epsilon*t=\delta$ .

Edit:Det ska stå 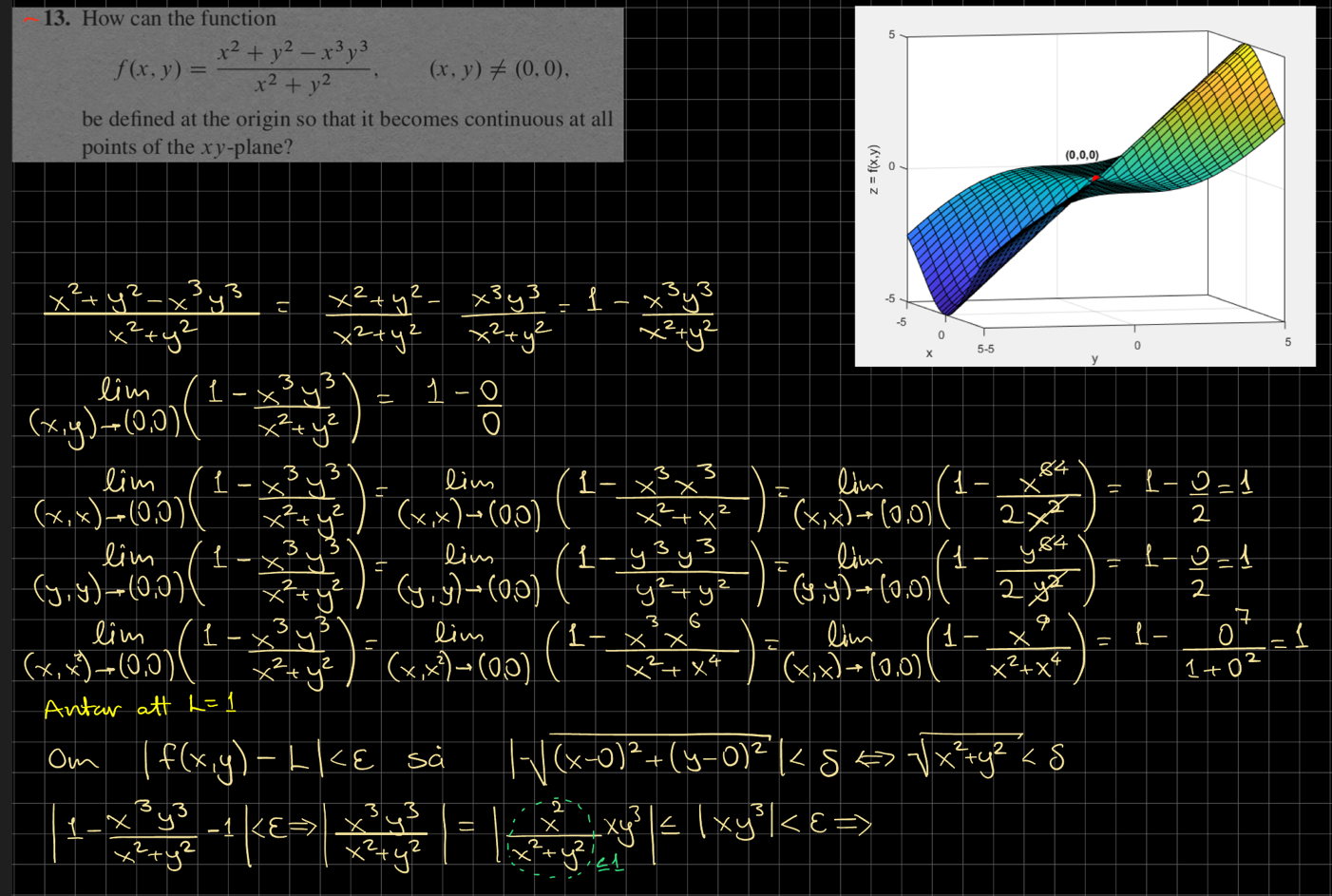$\sqrt{x^2+y^2} < \epsilon*t$ .

Jag är med på att vi kan skriva f = 1 - (x³y³)/(x²+y²)

så det gäller visa att andra termen går mot noll när (x,y) gör det.

För |x| < 1 och |y| < 1 har vi

| x³y³ / (x²+y²) | ≤ |y³| / (x²+y²) = |y| y²/(x²+y²) ≤ |y| som går mot noll när y går mot noll.

Och om (x,y) går mot noll så gör y det också.

Ursäkta pluttiga absoluttecken, det var vad som fanns.

Mogens skrev:
Jag är med på att vi kan skriva f = 1 - (x³y³)/(x²+y²)

så det gäller visa att andra termen går mot noll när (x,y) gör det.

För |x| < 1 och |y| < 1 har vi

| x³y³ / (x²+y²) | ≤ |y³| / (x²+y²) = |y| y²/(x²+y²) ≤ |y| som går mot noll när y går mot noll.

Och om (x,y) går mot noll så gör y det också.

Ursäkta pluttiga absoluttecken, det var vad som fanns.

Går det att visa med delta epsilon? känns mer absolut att lösa på det sättet

Tag 0<r<1 godtyckligt. För (x,y) tillhörande en omgivning kring (0,0) med radien d = r/2 gäller samma olikhet som Mogens skrivit ovan, alltså abs(f(x,y))<= abs(y)<=d=r/2<r Till r har vi alltså funnit ett d sådant att f avbildar en d-omgivning till origo in i en r-omgivning kring 0.

Eftersom jag ej har grekiska tecken har jag använt r för epsilon och d för delta - i övrigt ingen skillnad.

Lägg märke till att de nödvändiga uppskattningarna fortfarande måste till, så epsilon-delta är ingen tekniki/genväg att lösa uppgiften.

Epsilon-delta används för att exakt definiera begreppet gränsvärde/kontinuitet för funktioner på ett metriskt rum X (metriskt betyder att det finns ett avståndsbegrepp t ex absolutbelopp i Rⁿ)

Svara Avbryt

Visa senaste svar