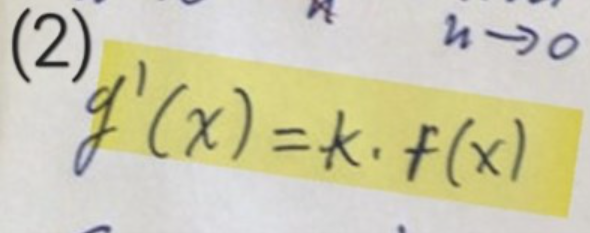Visa att g'(x)= k*f'(x)

$g'(x)=\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}=$
$\lim_{h\to 0}\frac{k\cdot f(x+h)-k\cdot f(x)}{h}=...$

Är det så här ?

f'(x) är 2, det stämmer. Men sen har du bara upprepat uppgiften. Att g'(x) = kf'(x) är det du ska visa.

Använd derivatans definition på g(x).

Jan du visa ?

Utgå från det tomast80 skrev i svar #2, använd sedan det som kom fram i slutet av denna tråd (rörande konstanter i gränsvärdesuttryck) 

jag förstår inte vad k är i det  här fallet

ska det vara k*f(x+h)-kf(x)

Arup skrev:

jag förstår inte vad k är i det  här fallet

 I uppgiften står det att k är en konstant och att du ska ta reda på vad $g'(x)$ är.

Enligt derivatans definition så är $g'(x)=\lim_{h\rightarrow0}\frac{g(x+h)-g(x)}{h}$

Eftersom det i uppgiften står att $g(x)=k\cdot f(x)$ så blir din "faktaruta"

=========

• $g(x)=k\cdot f(x)$
• $g(x+h)=k\cdot f(x+h)$

=========

Arup skrev:

ska det vara k*f(x+h)-kf(x)

Der beror på vad du menar. Om du menar täljaren i differenskvoten så är svaret ja.

Yngve skrev:

Utgå från det tomast80 skrev i svar #2, använd sedan det som kom fram i slutet av denna tråd (rörande konstanter i gränsvärdesuttryck) 

Derivstan för alla konstanter är noll

Ja, men derivatan av en konstant multiplicerat med en funktion är lika med konstanten multiplicerat med derivatan av funktionen.

Enligt formelbladet (gulmarkerat):

yngve på ändringkvotens täljare är det möjligt att bryta ut
$k$

Är det här en bra lösning ?

Nej, den stämmer inte.

Se markering, det du har kommit fram till är att g'(x) = k, men det stämmer inte.

Titta igenom din uträkning och se om du hittar felet.

jag ser inte felet. Jag har väl motiverat alla mina steg tydligt.

Är du med på att det du har visat är att g'(x) = k?

ja

OK bra. Är du med på att du sedan skriver att g'(x) är något helt annat?

nej, inte helt.

Vad är det ?

I det gulmarkerade söger du att g'(x) = k.

I det rödmarkerade säger du att g'(x) = k*(2x-3).

Det är inte samma sak.

Och tyvärr är inget av dessa rätt, du skulle ju visa att g'(x) = k*f'(x).

Och om du visar att f'(x) = 2 så räcker det med att du visar att g'(x) = k*2.

Hur då i uppgifts texten skulle jag väl visa att

$g\text{'}\left(x\right)=k\times f\text{'}\left(x\right)$

Arup skrev:

Hur då i uppgifts texten skulle jag väl visa att

$g\text{'}\left(x\right)=k\times f\text{'}\left(x\right)$

Ja det stämmer.

Men det du har kommit fram till är

• dels att g'(x) = k (det gulmarkerade).
• dels att g'(x) = k*f(x) (det rödmarkerade).

Är du med på det?

ja

OK, är du då med på att din lösning är fel?

nej

för att f(x) är väl 2x-3

eller dens derivata är ju 2

Arup skrev:

nej

för att f(x) är väl 2x-3

Ja, f(x) = 2x-3. Det är givet i uppgiften.

Arup skrev:

eller dens derivata är ju 2

Ja, f'(x) = 2 

Det bör du visa med hjälp av derivatans definition.

Säg till om det är för rörigt, då kan jag föreslå en lösningsmetod.

ok kör på

Jag ser två olika tillvägagångssätt:

=======

Det ena är följande:

1. Visa med hjälp av derivatans definition att f'(x) = 2.
2. Visa, med hjälp av derivatans definition, att g'(x) = k*2
3. Det betyder att g'(x) = k*f'(x), vilket skulle visas.

========

Det andra är följande:

1. Sätt upp ett uttryck för g'(x) enligt det tomast80 skrev i svar #2.
2. Motivera att det går att bryta ut konstanten k från detta uttryck, t.ex. på det sätt jag hänvisade till i svar #6.
3. Det ger dig att $g'(x)=k\cdot\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$, vilket per definition är lika med $k\cdot f'(x)$, vilket skulle visas.

Smart

Lös gärna uppgiften på båda sätten.

========

Har du hittat felen du gjorde tidigare?

Om inte, vill du hitta dem eller ska vi släppa det?

Yngve skrev:

Lös gärna uppgiften på båda sätten.

========

Har du hittat felen du gjorde tidigare?

Om inte, vill du hitta dem eller ska vi släppa det?

varför skulle jag släppa det ?

Bra!

Vill du fortsätta att försöka hitta felet själv (bra träning) eller vill du att jag pekar ut det?

pekar ut helst

Arup skrev:

pekar ut helst

Det gulmarkerade vid (1):

(2x+h)-3 är inte lika med f(x+h)

Det gulmarkerade vid (2):

Här skriver du att g'(x) = k*f(x), vilket inte stämmer.

Behöver du mer hjälp med något här?

Yngve skrev:

Behöver du mer hjälp med något här?

oj jag hade helt glömt uppgiften. Jag var bortrest idag. Jag kan se om jag kan ladda upp en ny bild med lösning idag alt. imorron bitti :D

Undrar dock vad som är fel med (2) här :

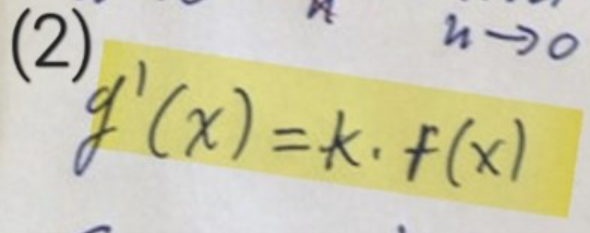
Tja, det stämmer ju inte. Vad fick du det ifrån?

Laguna skrev:

Tja, det stämmer ju inte. Vad fick du det ifrån?

ok, vad ska vara rätt uttryck ?

Jag tycker vi backar tills vi ser vad som gick fel.

Arup skrev:

Undrar dock vad som är fel med (2) här :

Varför tror du att det är rätt?

Jag ser inget i din uträkning som leder fram till detta påstående.

Skulle det här kunna förbättras ?

Snyggt!

En sak kan förbättras på sista raden: Skriv

$g'(x)=k\cdot\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}=k\cdot f'(x)$

Yngve skrev:

Snyggt!

En sak kan förbättras på sista raden: Skriv

$g'(x)=k\cdot\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}=k\cdot f'(x)$

Är inte det samma sak som jag skrev ?

Arup skrev:

Är inte det samma sak som jag skrev ?

Nej, du skrev så här:

Jag saknar mellansteget jag beskrev i svar #47.

Tycker du jag ska göra om uppgiften ?

Bara om du känner att du vill öva på skrivsätten.