Visa att funktion har gränsvärde i punkt

Vilken definition är det som åsyftas med "visa utifrån definitionen"? Gamla goda epsilon-delta kriteriet?

naytte skrev:

Vilken definition är det som åsyftas med "visa utifrån definitionen"? Gamla goda epsilon-delta kriteriet?

Jo, det antar jag. Lite otydligt skrivet i uppgiften tyvärr

Okej. Vi ska alltså bevisa klämsatsen om jag har förstått det rätt?

Börja i så fall med att skriva upp den givna informationen och skriv också upp vad vi vet om $f$ och $g$ uttryckt i $\epsilon$-$\delta$-definitionen.

naytte skrev:

Okej. Vi ska alltså bevisa klämsatsen om jag har förstått det rätt?

Börja i så fall med att skriva upp den givna informationen och skriv också upp vad vi vet om $f$ och $g$ uttryckt i $\epsilon$-$\delta$-definitionen.

filippahog skrev:

naytte skrev:

Okej. Vi ska alltså bevisa klämsatsen om jag har förstått det rätt?

Börja i så fall med att skriva upp den givna informationen och skriv också upp vad vi vet om $f$ och $g$ uttryckt i $\epsilon$-$\delta$-definitionen.

Tillägg:

Sats 3.1.16 är inte tillämpbar här, av samma skäl som igår. Men du har skirivt upp rätt information, bra!

En liten detalj är att vi måste motivera att det är samma $\delta$ här:

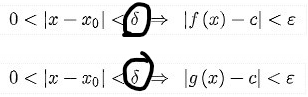
Men det är inget jätteproblem eftersom vi, precis som igår, bara kan låta vårt "gemensamma" $\delta$ vara det mindre av de två.

Vi vet att $f(x) \le h(x) \le g(x)$, varur det följer att $|f(x) - c| \le |h(x) - c| \le |g(x)-c| < \varepsilon$, när $|x-x_0| < \delta$. Detta betyder att $|h(x) - c| < \varepsilon$. 

Vi har alltså givet att:

$\displaystyle (\forall\varepsilon>0)(\exists\delta_1>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta_1\implies |f(x)-c|<\varepsilon]\;\; (1)$

$\displaystyle (\forall\varepsilon>0)(\exists\delta_2>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta_2\implies |g(x)-c|<\varepsilon]\;\; (2)$

Utifrån detta kan vi, enligt resonemanget ovan, dra slutsatsen att:

$\displaystyle (\forall\varepsilon>0)(\exists\delta>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta\implies |h(x)-c|<\varepsilon]$

där $\delta := \min\{\delta_1, \delta_2\}$

naytte skrev:

Sats 3.1.16 är inte tillämpbar här, av samma skäl som igår. Men du har skirivt upp rätt information, bra!

En liten detalj är att vi måste motivera att det är samma $\delta$ här:

Men det är inget jätteproblem eftersom vi, precis som igår, bara kan låta vårt "gemensamma" $\delta$ vara det mindre av de två.

Vi vet att $f(x) \le h(x) \le g(x)$, varur det följer att $|f(x) - c| \le |h(x) - c| \le |g(x)-c| < \varepsilon$, när $|x-x_0| < \delta$. Detta betyder att $|h(x) - c| < \varepsilon$. 

Vi har alltså givet att:

$\displaystyle (\forall\varepsilon>0)(\exists\delta_1>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta_1\implies |f(x)-c|<\varepsilon]\;\; (1)$

$\displaystyle (\forall\varepsilon>0)(\exists\delta_2>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta_2\implies |g(x)-c|<\varepsilon]\;\; (2)$

Utifrån detta kan vi, enligt resonemanget ovan, dra slutsatsen att:

$\displaystyle (\forall\varepsilon>0)(\exists\delta>0)(\forall x\in(a,b)\setminus\{ x_0 \})[|x-x_0|<\delta\implies |h(x)-c|<\varepsilon]$

där $\delta := \min\{\delta_1, \delta_2\}$

Herregud, jag är ledsen; det är den här definitionen jag går efter :')

Men tack igen för hjälpen. Jag uppskattar

Ingen orsak!

Men förstår du lösningen fullt ut? Är det något som är oklart?

naytte skrev:

Ingen orsak!

Men förstår du lösningen fullt ut? Är det något som är oklart?

Jo, jag förstår. Jag var förvirrad för att jag trodde lösningen skulle vara mer komplicerad, men egentligen är principen väldigt lik den andra uppgiften jag hade problem med