Visa att f har en invers
Halloj!
Jag sitter med frågan nedan:
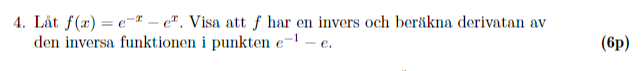
Jag tänker att man måste visa att f är en bijektion, av vilket det nödvändigtvis följer att f:Df→KDf är inverterbar. Jag börjar med att försöka visa injektivitet, alltså att för alla a,b∈Df så har vi att f(a)=f(b)⇔a=b. Då f är kontinuerlig på hela sin definitionsmängd kan vi ta fram dess derivata:
f'
Vi ser att derivatan är strikt negativ, vilket innebär att är strikt avtagande på hela sin definitionsmängd. Detta betyder att mappar exakt ett element ur sin definitionsmängd till exakt ett element ur sin målmängd, vilket inebär att:
Detta slutför beviset.
För surjektiviteten måste vi visa att , och detta följer trivialt av att enbart består av bilden av under (eftersom inget annat har specificerats i uppgiften). Detta slutför beviset.
Då är både injektiv och surjektiv måste den vara inverterbar, alltså existerar inversfunktionen.
Jag undrar om jag har gjort rätt här?
Man kan också visa att värdemängden är R. Så även om man antog att målmängden var hela R så funkar det.
Det köper jag. Men är det rätt så som jag har gjort också? Jag blir lite fundersam för i facit har de bara beviset injektivitet. Fattar inte varför de kan skippa surjektiviteten:
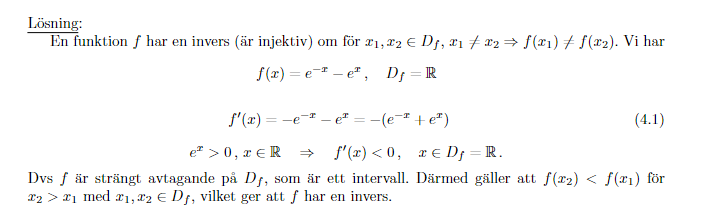
Det här stämmer väl inte? De har väl visat att vänsterinversen finns, men inte att inversen finns?
Ja, om man inte angett målmängd så går det inte att säga om funktionen är surjektiv eller inte. Man har ju dessutom inte angett vad Df är. Det står i facit att Df är ett intervall, men hur skulle man veta det.
Så man får anta att målmängden är samma som värdemängden eller nöja sig med att konstatera att det finns vänsterinvers.
Hursomhelst så är väl f(x) = -2sinh(x). Så inversen borde bli f-1(x) = sinh-1(-x/2).



