Visa att elektriskt fält är konstant mellan laddade plattor

Hej, till situationen nedan, två parallella plattor där övre har laddning +q och nedre -q. Vill ta fram det elektriska fältet mellan. Gör en Gauss yta som täcker ena plattan och använder mig av Gauss lag på integralform. Det elektriska fältet pekar i $-\hat{z}$ riktning, och normalen till de övre Gausslocket har motsatt riktning på normalen $+\hat{z}$ riktning. Vi får därför -EA för det övre locket. På samma sätt för det undre locket, här dock är elektriska fältet och normalen i samma riktning, vi får +EA. Summan blir alltså 0, vilket det inte bör. Vad missar jag?

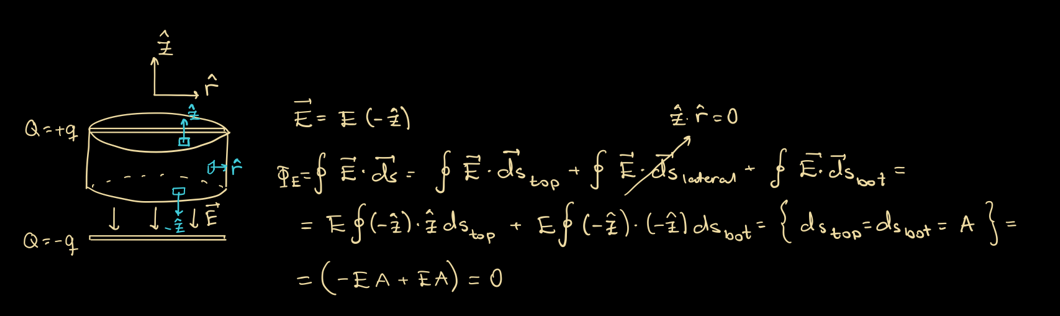
Hej!

Du måste också anta att plattorna har oändlig utsträckning, annars är inte fältet från plattan alltid vinkelrätt mot plattan.

Men det var inte svar på din fråga. Svaret på din fråga är att du gör fel antagande om fältets utseende. Fältet pekar utåt från den positiva plattan, på båda sidorna av plattan (och tvärtom på den negativa). Räkna på en platta i taget.

Titta på den här videon så tror jag att du förstår:

https://youtu.be/gsmigo2stQA?si=6_hOkKpUINR3erwn

JohanF skrev:
Hej!

Du måste också anta att plattorna har oändlig utsträckning, annars är inte fältet från plattan alltid vinkelrätt mot plattan.

Men det var inte svar på din fråga. Svaret på din fråga är att du gör fel antagande om fältets utseende. Fältet pekar utåt från den positiva plattan, på båda sidorna av plattan (och tvärtom på den negativa). Räkna på en platta i taget.

Titta på den här videon så tror jag att du förstår:

https://youtu.be/gsmigo2stQA?si=6_hOkKpUINR3erwn

Tack, bra video. Tror jag är med nu

Är plattorna ledande, e.g. metallplattor? Eller skall man se det hela som två laddningsbärande ytor, där laddningarna är fixerade på ytorna?

PATENTERAMERA skrev:
Är plattorna ledande, e.g. metallplattor? Eller skall man se det hela som två laddningsbärande ytor, där laddningarna är fixerade på ytorna?

Visste inte det var någon skillnad på det två situationerna. Om plattorna är två metallplattor, som i en kondensator, gäller något annorlunda då?

Ja, det blir lite annorlunda.

Tillägg: 12 dec 2024 19:31

Om du har en metallplatta (ledande platta) så är fältet inne i plattan noll. Du kan ha en ytladdningstäthet på undersidan och en annan på översidan. Så i princip kan du få fyra parallella ytor med laddning.

Tillägg: 12 dec 2024 23:45

Om du vill lösa detta problem så försök först att visa att $σ_{1 a} = - σ_{2 a}$ och $σ_{1 b} = σ_{2 b}$ .

Sedan gäller naturligtvis att $σ_{1 a} + σ_{1 b} = Q_{1} / A$ och $σ_{2 a} + σ_{2 b} = Q_{2} / A$ .

Bonne Chance!

Svara

Visa senaste svar