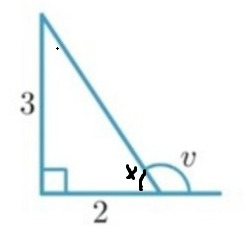
Vinkeln v

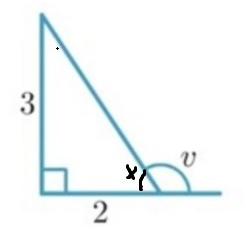
I figuren ser vi att $x+v$ bilar en vinkeln på 180 grader, dvs:

$x+v=180$

Dracaena skrev:

I figuren ser vi att $x+v$ bilar en vinkeln på 180 grader, dvs:

$x+v=180$

Ja, det är jag med på. Därför tänkte jag att om man räknar ut vinkeln x så subtraherar man den sedan

180-x = v

När vi fått ut vinkeln v, vet jag dock inte riktigt hur jag ska ta mig vidare, på grund av att vinkeln är större än 90⁰ och de trigonometriska formlerna (sin, cos, tan) inte riktigt att går använda.

Måste ha något med enhetscirkeln att göra då väl? 

Jag var lite vag i mitt svar eftersom jag inte ville ge dig svaret. 

Du har tänkt rätt, vi behöver inte blanda in enhetscirkeln. Den inre vinkeln, det jag kallade $x$ i figuren är mindre än 90 grader. Den yttre vinkeln är mycket riktigt den inre vinkeln subtraherad från 180 grader. 

Jag är inte riktigt säker på hur du vill använda sin, cos eller tan för att beräkna v? Du var väl med på att $x+v=180$ som ger: $v=180^\circ-x$, och $x=\arctan(3/2) \approx 56.3 ^\circ$

Så hur stor är vinkeln $v$?

Dracaena skrev:

Jag var lite vag i mitt svar eftersom jag inte ville ge dig svaret. 

Du har tänkt rätt, vi behöver inte blanda in enhetscirkeln. Den inre vinkeln, det jag kallade $x$ i figuren är mindre än 90 grader. Den yttre vinkeln är mycket riktigt den inre vinkeln subtraherad från 180 grader. 

Jag är inte riktigt säker på hur du vill använda sin, cos eller tan för att beräkna v? Du var väl med på att $x+v=180$ som ger: $v=180^\circ-x$, och $x=\arctan(3/2) \approx 56.3 ^\circ$

Så hur stor är vinkeln $v$?

180-56,3 ≈ 123,7⁰

Cos(123,7) ≈ -0,55

Av en konstig anledning skrev jag sin istället för cos innan 

Tack snälla!

Uppgiften var att bestämma cos v exakt.

Alltså - 2/$\sqrt{13}$ (med Pythagoras sats).

Louis skrev:

Uppgiften var att bestämma cos v exakt.

Alltså - 2/$\sqrt{13}$ (med Pythagoras sats).

Hur fick du fram det exakta värdet med Pythagoras sats?

Hypotenusan är $\sqrt{2^2+3^2}$= $\sqrt{13}$.

Louis skrev:

Hypotenusan är $\sqrt{2^2+3^2}$= $\sqrt{13}$.

Ja, det är jag med på. Men varifrån kommer -2?

Är du med på att man använder sambandet cos(180-v) = -cos(v)?

och att cos(v) är (närstående katet)/hypotenusa ?

Jag var lite slarvig, jag såg bilden och antog direkt att detta var en klassisk matte 1 uppgift där man ska beräkna den yttre vinkeln. Det borde har varit en ledtråd att jag inte läst uppgiften tillräckligt noga när du började prata om enhetscirkeln.

Ture skrev:

Är du med på att man använder sambandet cos(180-v) = -cos(v)?

Ja, men inte hur man kan få nytta av det här

och att cos(v) är (närstående katet)/hypotenusa ?

Japp

Tillägg: 3 aug 2023 18:51

Vinkeln v är cirka 123,7⁰

naturnatur1 skrev:

Ture skrev:

Är du med på att man använder sambandet cos(180-v) = -cos(v)?

Ja, men inte hur man kan få nytta av det här

180-v = x i din figur ! Så:  -cos(v) = cos(180-v) = cos(x)

och att cos(v) är (närstående katet)/hypotenusa ?

Japp

Då kan du beräkna cos(x) exakt 

---

Tillägg: 3 aug 2023 18:51

Vinkeln v är cirka 123,7⁰

Jo, men som Louis skrev så ska vi svara exakt, och då duger det inte med närmevärden på vinklarna.

Ture skrev:

naturnatur1 skrev:

Visa föregående citat

Ture skrev:

Är du med på att man använder sambandet cos(180-v) = -cos(v)?

Ja, men inte hur man kan få nytta av det här

180-v = x i din figur ! Så:  -cos(v) = cos(180-v) = cos(x)

Visa föregående citat

och att cos(v) är (närstående katet)/hypotenusa ?

Japp

Då kan du beräkna cos(x) exakt 

---

Tillägg: 3 aug 2023 18:51

Vinkeln v är cirka 123,7⁰

Jo, men som Louis skrev så ska vi svara exakt, och då duger det inte med närmevärden på vinklarna.

Där vinkeln v finns kan man väl inte använda sig utav Pythagoras sats eller trigonometriska formler (sin, cos, tan) pga den triangeln inte är rätvinklig?

Jag hänger med på att man kan göra det där vinkeln x finns (3^2 och 2^2). Men vet inte riktigt hur jag ska ta mig vidare med det sambandet. 

Fick bara fram nörmevärdet, men lyckas inte få fram -2/√13

Du fick fram närmevärdet via närmevärdet på v.
Men du behöver inte alls fundera på värdet på v.
De frågar inte heller efter v.

cos x = 2/$\sqrt{13}$

cos v = -cos(180-v) = -cos x = -2/$\sqrt{13}$

där jag satt samman sambanden som du fick av Ture.

Louis skrev:

Du fick fram närmevärdet via närmevärdet på v.
Men du behöver inte alls fundera på värdet på v.
De frågar inte heller efter v.

cos x = 2/$\sqrt{13}$

cos v = -cos(180-v) = -cos x = -2/$\sqrt{13}$

där jag satt samman sambanden som du fick av Ture.

Vart kommer 2/ ifrån? (Täljaren) 

Tillägg: 3 aug 2023 19:48

Jag tror jag hänger med, återkommer

cos x = närstående katet/hypotenusa.

Närstående katet = 2

Tack för hjälpen alla i denna tråd!