Vilket värde på k ska han använda?
Hej! Jag försöker lösa a-uppgiften men vet inte riktigt hur man kan göra, jag har försökt göra så som på bilden nedan, men har även försökt approximera till en normalfördelning och lösa det på så vis, verkar ändå inte få rätt svar dock:( En approximation jag försökt använda är N(np;np(1-p)) men denna approximation kanske inte gäller då tumregeln för att använda denna aproximation skulle vara att np(1-p)>10 men np(1-p) =100*0,02*0.98= 1,96<10. En annan approximation jag försökt med är summan av xi1,...xi100 approximativt är N(n*my,sigma*sqr(n))=N(100*2;1,4*sqr(100)) = N(2;14) men får även fel svar då jag använder denna approximation (andra bilden nedan).
Facit:
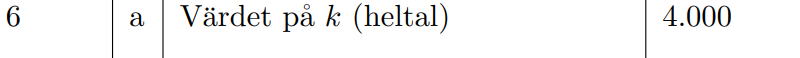
Lösning 1:

Lösning 2:

Tack på förhand!
Hur lyder uppgiften?
Arktos skrev:Hur lyder uppgiften?
Oj vad dumt jag hade glömt lägga in screenshoten för frågan! Förlåt!
Här är själva frågan:)

Räkna med exakta fördelningen, det kommer bli ett fåtal termer att addera (k litet) eftersom det är mer än 50% sannolikhet för k=2 (medelvärdet som i det här fallet också är median).
Dessutom kan du återanvända värdet för ett k till nästa då du bara lägger till en term i summan som är CDF för binomialfördelningen.
dioid skrev:Räkna med exakta fördelningen, det kommer bli ett fåtal termer att addera (k litet) eftersom det är mer än 50% sannolikhet för k=2 (medelvärdet som i det här fallet också är median).
Dessutom kan du återanvända värdet för ett k till nästa då du bara lägger till en term i summan som är CDF för binomialfördelningen.
Tack för svar! Jag förstår dock inte riktigt hur du menar?
P(xi <= k) = sum(from m=0, to m=k, binom(n, m) p^m (1-p)^(n-m))
binom(n, m) är binomialkoefficienten ”n över m”
Så för k=0 är det bara en term i summan, 0.98^100. För k=1, två termer, ena är samma som för k=0 och. Andra är 100*0.02*0.98^99. Så genom att addera termer får du sannolikheten för allt större värden på k. Upprepa tills du kommer upp till 0.95 och det värdet på k är svaret på frågan.
dioid skrev:P(xi <= k) = sum(from m=0, to m=k, binom(n, m) p^m (1-p)^(n-m))
binom(n, m) är binomialkoefficienten ”n över m”
Så för k=0 är det bara en term i summan, 0.98^100. För k=1, två termer, ena är samma som för k=0 och. Andra är 100*0.02*0.98^99. Så genom att addera termer får du sannolikheten för allt större värden på k. Upprepa tills du kommer upp till 0.95 och det värdet på k är svaret på frågan.
Ahh tack nu förstår jag och får rätt svar med de beräkningarna! tack:)

