Vilken summa är mest sannolik att du kommer få av talen som kommer upp?
Du kastar två 6-sidiga tärningar. Vilken summa är mest sannolik att du kommer få av talen som kommer upp och hur stor är denna sannolikhet?
Jag behöver hjälp med den här uppgiften (hela frågan fick inte plats i rubriken). Sannolikhet och kombination har aldrig varit min styrka och jag förstår inte riktigt hur jag ska gå tillväga.
Jag började med att försöka räkna ut svaret genom formeln för kombinationer: C(n,k) = n!/(n-k)!k! , där n motsvarar hur många objekt totalt sett, och k motsvarar hur många man väljer. Problemet är de att jag har ju flera objekt, eller är "objekten" endast de två tärningarna eller alla olika kombinationer?
Jag tänkte även att man på något sätt skulle kunna rita upp ett koordinatsystem, liknande de nedan (om du zoomar ser du värdena bättre). 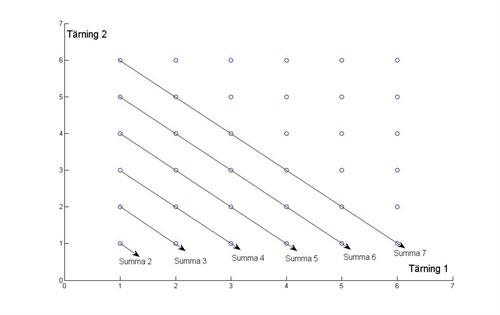
Men problemet är att det finns ju hur många kombinationer direkt, man kan ju få 1 och 2, 1 och 3, 1 och 4 osv. Jag tänker att det borde finnas en slags formel, eller iallafall ett lättare sätt att gå tillväga istället för att försöka rita upp alla siffror och se vilka man kan kombinera med varandra?
Väldigt tacksam för hjälp :)
Koordinatsystemet, som vi kan kalla "utfallsrum" (eftersom det visar alla möjliga utfall) är alldeles utmärkt!
Varje prick motsvarar ett utfall.
Det finns alltså 6*6 = 36 olika utfall, alla lika sannolika.
De pilar som är ritade binder samman de utfall vars ögonsumma är lika.
Det finns bara ett sätt att få summan 2, nämligen (T1:T2) = (1:1)
Det finns två sätt att få summan 3, nämligen (T1:T2) = (1:2) eller (2:1)
Och så vidare.
Frågan i uppgiften kokar då ner till följande:
Vilken pil är längst och hur stor andel av de 36 prickarna täcker den?
I det här fallet så tycker jag att rita upp en tabell som du gjort med varje utfall som finns är en väldigt bra strategi. Precis som du ritat upp så kan du se tydligt att det är ett utfall (en summa) som ser ut att vara vanligast vid kast med två tärningar.
För att få fram en sannolikhet så behöver du nu bara dividera antalet utfall som ger denna summa på det totala antalet av möjliga utfall.
Exakt, då är det ju summan 7 som är vanligast, och den täcker 6/36 prickar.
Om jag har förstått det rätt ska jag dividera 6 med 36 (antalet utfall/de totala antalet möjliga utfall), vilket blir ungefär 16.66%.
Helt rätt.
Det är störst sannolikhet att få summan 7 är och den sannolikheten är 1/6, dvs ungefär 17 %.
Okej, tack så mycket för hjälpen.


