vilken fördelning får summan av två exponentialfördelade variabler?
Hej!
Jag försöker lösa denna uppgift men vet inte riktigt hur jag ska göra. Jag tänker att jag kan sätta xi1+xi2 till en variabel eta och om jag bestämmer dess fördelning kan jag sedan beräkna sannolikheten att eta är mindre än eller lika med 1. Frågan är dock hur jag ska ta fram dess fördelning?
Jag vet att V(eta)= V(xi1)+V(xi2) =
och E(eta) =
Dock vet jag inte vilken fördelning eta får? eta består ju av två variabler som båda är exponentialfördelade men även om eta är summan av dessa, blir eta också exponentialfördelad?
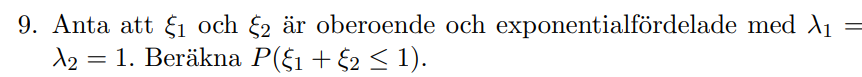
Tack på förhand!
Efter litet googling får jag veta att summan inte är exponentialfördelad, den är gammafördelad.
Att de är gammafördelade kan visas genom att undersöka just P(X1+X2<x), utnyttja oberoende och använda sig av lite regler för väntevärden. Detta blir lite långt att göra på en tenta, men kan vara en bra uppgift att träna på
Annars gissar jag att tanken är att du kan använda satsen direkt utan bevis.
Laguna skrev:Efter litet googling får jag veta att summan inte är exponentialfördelad, den är gammafördelad.
Ah okej! Men gäller detta bara summan av exponentialfördelade variabler eller även andra?
Calle_K skrev:Att de är gammafördelade kan visas genom att undersöka just P(X1+X2<x), utnyttja oberoende och använda sig av lite regler för väntevärden. Detta blir lite långt att göra på en tenta, men kan vara en bra uppgift att träna på
Annars gissar jag att tanken är att du kan använda satsen direkt utan bevis.
Har dock inte sett satsen i boken:(
Summan av n stycken oberonde Exp(lambda) variabler är G(n,lambda)-fördelade.
T.ex kommer summan av n stycken Bernoulli(p) variabler vara Binomial(n,p) fördelade.
Calle_K skrev:Summan av n stycken oberonde Exp(lambda) variabler är G(n,lambda)-fördelade.
T.ex kommer summan av n stycken Bernoulli(p) variabler vara Binomial(n,p) fördelade.
Ah okej tack!



