Vietes formler

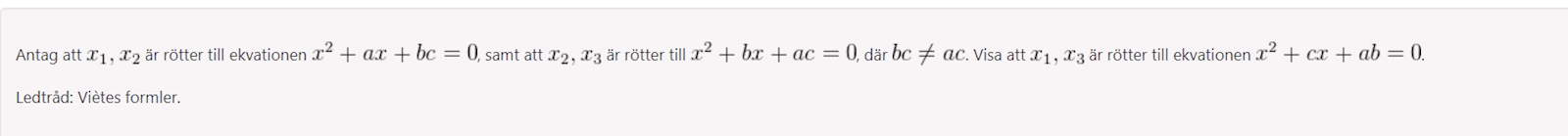
Jag har det svårt att visa detta, från vietes formler vet vi att x1+x2 = -a och x2+x3 = -b samt x1x2 = bc och x2x3=acvi vill visa att x1+x3=-c och x1*x3=ab

Vid addition får jag x1+x2 + x2+x3 = -a-b -> x1+x3 = -a-b-2*(x2)jag har svårt att visa att -c = -a-b-2*(x2), har testat typ alla kombinationer som finns och kan inte få -c explicit med hjälp av formlerna.samma för x1x3 = ab -> x1x3 = ab*c^2/(x2)^2 när jag multiplicerar x1x2 * x2x3 = bc*ac. det känns omöjligt. Flera timmar och kan inte knäcka det. kan inte få ab explicit/algebraiskt:

Så jag försökte visa att detta är sant om x2 = c:

Detta är min lösning: vi vet från vietes formler att x1x2 = bc samt x2x3=ac, om vi multiplicerar detta får vi att x1*x2*x2*x3= bc*ac -> x1*x3 = ab*c^2/(x2)^2. och det vi vill få harifrån är att x1x3 = ab, så (x2)^2 måste vara lika med c^2. vi tar roten ur det och får att x2 är antingen +-c. Nu när vi multiplcerar (x1+x2)(x2+x3) får vi = -a*-b = ab. om vi utvecklar det vidare får vi:x1x3+x1x2+x2x3+(x2)^2 = ab, och för att detta ska vara sant, att x1x3=ab, behöver vi att x1x2+(x2)^2+x2x3 = 0. och från detta faktoriserar vi ut ett x2 och får x2(x1+x2+x3) = 0, sätter att detta ska vara lika med 0 för att få att x1x3=ab.så x2 får inte vara lika med 0 då vi kan ej dela med noll, då i början vi dividerade med (x2)^2. Så vi jobbar endast med : x1+x2+x3 = 0, och från det får vi att x1 + x3 måste vara lika med -x2, och vi behöver att x1+x3 vara lika med -c, så x2 måste vara lika med c.Slutsats: För att x1 och x3 ska vara rötter till x^2+cx+ab, behövs det alltså att x2 = -c.

Vet inte om det är korrekt tänkt eller ej. Kan inte riktigt visa det.
Tack!