Verkliga trigonometiska ekvationer
Hej, jag skulle räkna ut en vinkel för att sedan kunna räkna ut avståndet mellan två båtar som ligger på en rät linje.

Ekvationen ger sedan att med nollproduktsmetoden få en vinkel från cos(V)= 0 --> V= 90+ (360n) och tan v= 40.84 + (180n)
Detta var en vinkel i en triangel som innehöll vinklarna ( V, 150-V , U)
Det jag undrar är varför jag inte skulle kunna använda 90 grader istället för 40.84, som de använde i facit?
Din bild blev ingen bild.
herregud, testade igen men det funkade inte,
hursomhelst använde jag mig av sinussatsen och fick: sin(150-v)/1.3 = sin(v) / 0.9
och kom fram till:
< width="262" height="49" style="max-width: none; vertical-align: -18px;">
Tillägg: 23 sep 2021 12:16
aja, jag ger upp hahah,
fick att cos(v)=0
och att tan(v) = - 1/ (sqrt3 - 2.6/0.9)
Om vi ska kunna hjälpa så behöver vi veta hur uppgiften ser ut.
Ladda upp en bild eller beskriv den i text.
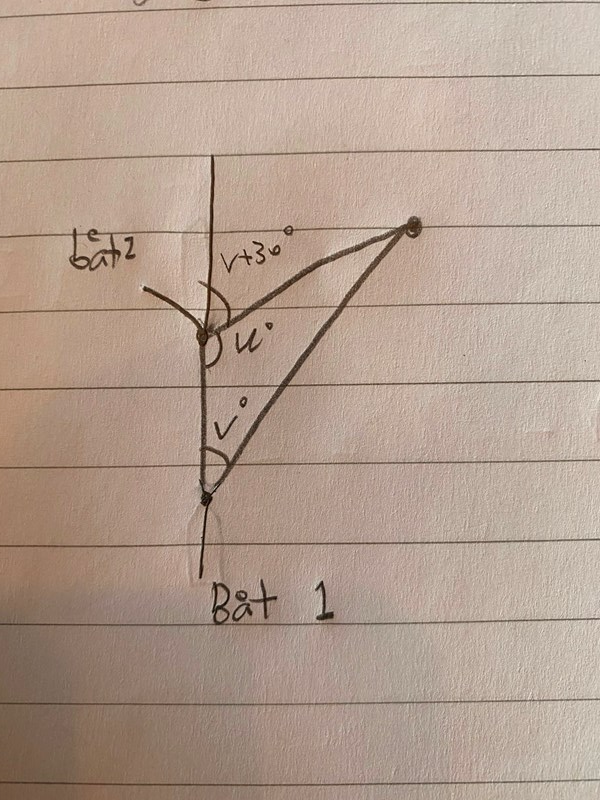
Så, la även till skissen av hur jag uppfattade uppgiften, är det orealistiskt att v= 90 och att man därför ska försumma den vinkeln?
Jag förstår varken hur du kom fram till cos(v) = 0 eller varför facit beräknar vinkeln v.
Med beteckningar enligt bilden så har vi att u = 180°-(v+30°) = 150°-v.
Eftersom u+v+w = 180° så får vi att w = 180°-(150°-v)-v = 30°.
Cosinussatsen ger oss då direkt att x2 = 0,92 + 1,32 -2•0,9•1,3•cos(30°).

==============
Men som svar på din fråga, ja det är orealistiskt att v = 90°. Försök att rita en sådan figur så får du se att det inte går ihop.



