Vektorer och gradienten
Hej, jag undrar vad skillnaden är på dessa två frågor jag bifogar. I båda uppgifterna har jag först räknat ut gradienten av en funktion, men jag förstår faktiskt inte riktigt vad gradienten är och varför skillanden blir som den blir i uppgiftena.
I den första "Value" så frågar dom om "maximal directional derivative at a point" och då ska slutresultatet bli en längd/ett värde. Är det längden av gradienten? Jag vet att gradientens riktning är dit riktningen är maximal, men varför blir det ett värde här?
Motsvarigheten, eller det jag blir förvirrad av, är i den andra uppgiften "Vector". Här frågar de om direktionen där funtionen i punkten ökar som mest och då ska svaret bli en vektor.
Varför blir svaret en vektor i det ena fallet och ett värde i det andra?
Tack, Olivia

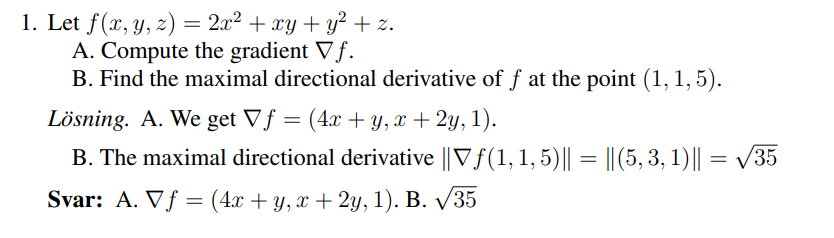
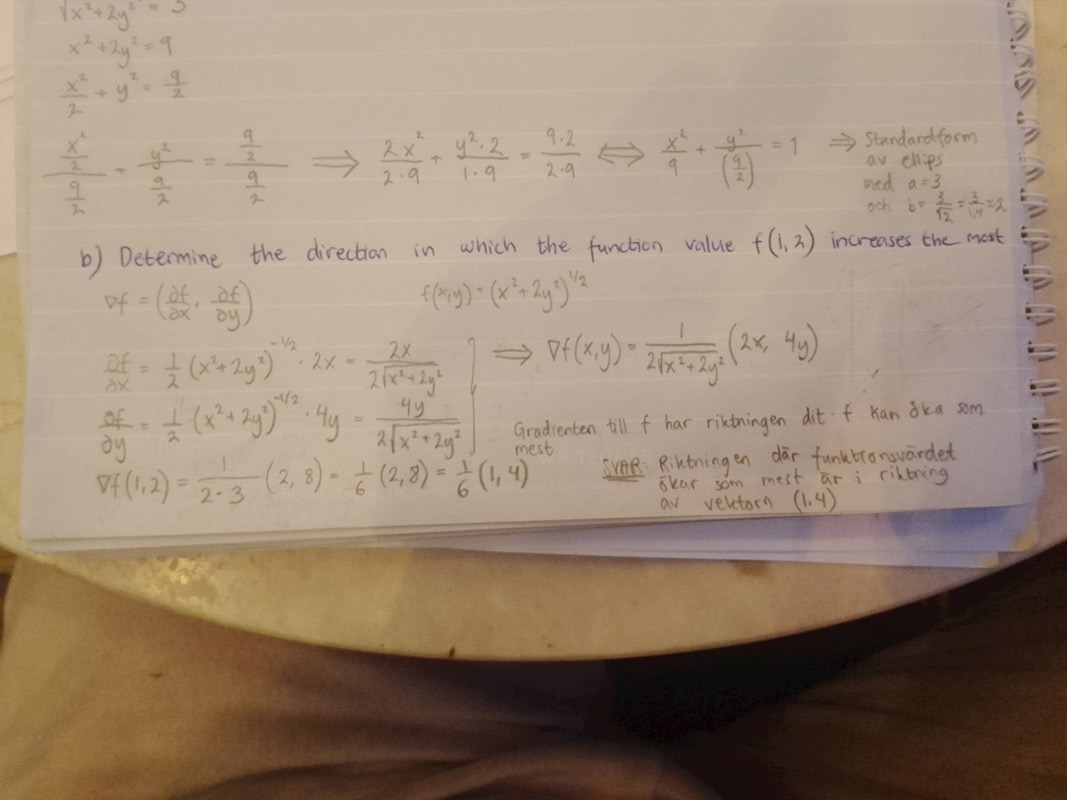

"directional derivative at a point" anger hur som funktionsvärdet förändras då man rör sig i en riktning från en punkt. Exempelvis kan man fråga sig hur som funktionen förändras om man befinner sig i (1,1,1) och rör sig i z-axelns riktning, trots att funktionen tycks vara mer föränderlig i exempelvis x-axelns riktning.
"maximal directional derivative at a point" är då det största värdet vi kan få fram då vi prövar alla möjliga riktningar att röra sig mot från. Att denna enkelt kan räknas ut med vanliga derivationsregler är något vi är tacksamma över. Att det blir ett värde beror på att en derivata är ett värde, som ges av längden av gradientvektorn.
I andra uppgiften så frågar de efter det engelska ordet "direction", på svenska "riktning". Det är svårt att peka ut en riktning med bara ett värde, så där är de faktiskt intresserad av gradienten som en vektor.
Bedinsis skrev:"directional derivative at a point" anger hur som funktionsvärdet förändras då man rör sig i en riktning från en punkt. Exempelvis kan man fråga sig hur som funktionen förändras om man befinner sig i (1,1,1) och rör sig i z-axelns riktning, trots att funktionen tycks vara mer föränderlig i exempelvis x-axelns riktning.
"maximal directional derivative at a point" är då det största värdet vi kan få fram då vi prövar alla möjliga riktningar att röra sig mot från. Att denna enkelt kan räknas ut med vanliga derivationsregler är något vi är tacksamma över. Att det blir ett värde beror på att en derivata är ett värde, som ges av längden av gradientvektorn.
I andra uppgiften så frågar de efter det engelska ordet "direction", på svenska "riktning". Det är svårt att peka ut en riktning med bara ett värde, så där är de faktiskt intresserad av gradienten som en vektor.
Tack så mycket, det gav bättre förståelse!

