Vattendjupet


 Hej! Jag undrar om jag har löst a uppgiften rätt. I b så undrar jag vad som krävs för att vattendjupet ska stiga eller sjunka som snabbast
Hej! Jag undrar om jag har löst a uppgiften rätt. I b så undrar jag vad som krävs för att vattendjupet ska stiga eller sjunka som snabbast
a) Dygnet har 24h och du fick svar med "+ 12n"
Tänk alltid på definitionsmängden för variabeln i denna typ av tal.
Du fick fram det ena av 2 intervall då djupet är >= 6 meter.
b)
y(t) är djupet.
Då är y'(t) förändringen av djupet.
Du vill veta när förändringen av djupet är störst (både ökning och minskning). Du vill alltså veta när y'(t) har sitt max- och minvärde. Hur gör du då?
a) Hur menar du med att du fick det ena av 2 intervall då djupet är > 6m? Vad ska jag göra för att hitta det andra intervallet?
b) Jag söker efter andraderivatan
a) Du har fått t1=4+12n och t2=0+12n. Då fick du intervallet 0 till 4. Vilket intervall får du med n=1?
Definitionsmängden för t är 0 <= t < 24 eftersom det är timmar under dygn.
Dessutom: De frågade efter intervall för t då y(t)>=6. Du löste y(t)=0 och fick gränserna.
Men man vet inte automatiskt på vilken sida om t=0 och t=4 som y(t)>=6.
Du bör motivera varför y(t) >= 6 i intervallet. T ex mha enhetscirklen eller genom att visa att y(t) har positiv derivata för t=0, i så fall är den över 6.
b) Ja. Extrempunkterna för en funktion får man genom att derivera och sätta lika med 0. Nu är funktionen vi vill undersöka y'(t) och dess derivata y''(t) så det blir andraderivatan av y(t).
Programmeraren skrev:a) Du har fått t1=4+12n och t2=0+12n. Då fick du intervallet 0 till 4. Vilket intervall får du med n=1?
Definitionsmängden för t är 0 <= t < 24 eftersom det är timmar under dygn.
Dessutom: De frågade efter intervall för t då y(t)>=6. Du löste y(t)=0 och fick gränserna.
Men man vet inte automatiskt på vilken sida om t=0 och t=4 som y(t)>=6.
Du bör motivera varför y(t) >= 6 i intervallet. T ex mha enhetscirklen eller genom att visa att y(t) har positiv derivata för t=0, i så fall är den över 6.b) Ja. Extrempunkterna för en funktion får man genom att derivera och sätta lika med 0. Nu är funktionen vi vill undersöka y'(t) och dess derivata y''(t) så det blir andraderivatan av y(t).
Om n=1 får jag t=16 och t=12
alltså 12 < t < 16
Men jag förstår inte . Varför ska man testa med olika värden på n?
Menar du att jag ska lösa ekvationen y(t)>6?
Du måste tänka på vad t är. Vilka värden t kan anta. Uppgiften säger "t är tiden i timmar räknat från midnatt".
Från #2:
"a) Dygnet har 24h och du fick svar med "+ 12n"
Tänk alltid på definitionsmängden för variabeln i denna typ av tal."
Från #4:
"Definitionsmängden för t är 0 <= t < 24 eftersom det är timmar under dygn."
Du har redan löst ekvationen y(t)>=6. Men du har bara angett ett av de två intervall då y(t)>=6 inom t:s defintionsmängd.
Det andra intervallet är 12<=t<=16.
Läs också vad jag skrev om att visa att intervallet ger y(t)>=6. Att bara räkna ut för vilka t som y(t)=6 visar inte det, det ger bara gränserna (de t) då y(t) går från mer/mindre än 6 till motsatsen.
Är det isåfall rätt att svara att
6>t>0
och då 16>t>12 ? jag undrar hur ska man kunna förstå varför man ska testa med olika värden på n? Kan du visa med hjälp av en graf?
 Det här är min ansats för b frågan. Men sen vet jag inte vad jag ska göra
Det här är min ansats för b frågan. Men sen vet jag inte vad jag ska göra
a) När du löste 6=5+2cos(v) så hittade du gränserna. Du använde dem för att göra ett internvall.
De frågar efter när 6 <= 5+2cos(v)
Det du fick fram nära rätt svar men eftersom du löser med "=" visar du inte på vilken sida om gränserna som olikheten gäller.
Olikheter och vinklar kräver att man tar reda på vilken sida av gränserna man hamnar på. Gränsvinklara är som du beräknade -1,047 och +1,047. Vi tittar i enghetscirkeln:
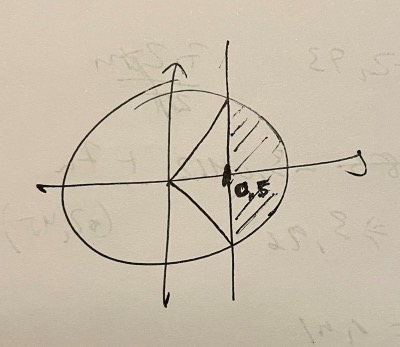
Här ser vi att de gränserna för de vinklar som ger cos(v)>=0,5 i hela området är v >= -1,047 och v <= 1,047.
Löser vi olikheterna
pi(t-2)/6 >= -1,047 och
pi(t-2)/6 <= 1,047 får vi
0 + 12n <= t <= 4 + 12n
Eftersom definitionsmängden för t är 0 <= t <24 får vi även 12 <= t <= 16.
Ritar vi upp grafen ser vi att det stämmer:

Du gör en olikhet men du söker extrempunkterna för f'(t), dvs då f''(t)=0.
b) f'(t) är förändringshastigheten. Du vill hitta när den är som hastigast, dvs min- och maxpunkterna för f'(t).
Derivatan av f'(t) är f''(t).
Sätter du f''(t)=0 får du fram extrempunkterna för f'(t).
Det är precis som ett vanligt tal där du ska hitta min och max.
Om det inte känns klart, testa att tänka så här:
Vi gör en ny funktion g(t) som ger djupförändringens hastighet.
När är hastigheten högst? Vi deriverar och sätter g'(t)=0 för att få min- och maxpunkterna
Vilken funktion är g(t)?
g(t)=f'(t) eftersom f'(t) är djupförändringens hastighet.
Och om g(t)=f'(t) så är g'(t)=f''(t).

