Variabelseparation
Uppgift: Lös med hjälp av variabelseparationsmetoden:
∂u∂t=∂2u∂x2,
0<x<π,
t>0
Kom fram till det här och behöver hjälp med att komma vidare!
Min lösning
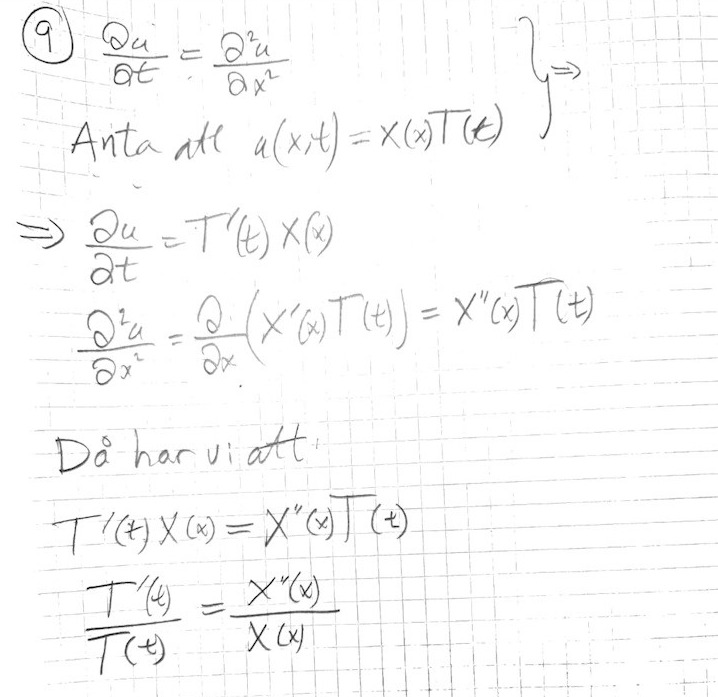
VL och HL av din sista ekvation är endast lika när de båda är konstanta, eftersom vänsterledet en funktion av endast en variabel t, och högerledet är en funktion av endast en variabel x.
Så nästa steg är att separera din sista ekvation i två differentialekvationer.
Okej! Jag är med på det nu!
då får jag:
T'
Där är en konstant. Vad ska jag ansätta för högerled nu?
Du kan nu börja lösa varje ekvation individuellt. Den första ekvationen (av första ordningen) kan skrivas så här:
Kan du gå vidare?
Multiplicerar både led med och integrerar:
Känns fel dock.
Jag har nu redigerat inlägget #4. Jag missade "d" (ber om ursäkt), så "dt" redan finns och du kan integrera direkt.
Blir det bara inte ?
Edit: sen löser man ut så att: , där ?
Skulle behöva hjälp med att fortsätta!
Lösning..

Är det din lösning du har lagt upp senast? Vilket är nästa steg du behöver hjälp med?
Japp det är det.
Jag tar ju fram och , sedan måste jag ju hitta kontanterna i respektive ekvation! Men vet inte riktigt hur.
Om vi bara tittar på ekvationssystemet du ställt upp så har vi inget roligare alternativ än att C=0 eller A,B=0, så det leder ju till att hela u är konstant. Om du har räknat rätt tidigare, men texten är ganska suddig och det är inte mitt område, så vet inte om det är så. Verkar rimligt räknat.
Som Micimacko säger, lite svårt att se din bild!
En fråga: En fråga: Är det allt som står i frågan? Det är ju värmeekvationen eller hur? Vilket är
dvs. en 1/k saknas?
Finns inga initiala villkor? Du behöver dem för att hitta de konstanterna.
OBS! För att stämmer överens med situationen kan du använda istället för c.
och i så fall får du:
Sedan blir lösningen X(t) gånger T(t), precis som du har gjort.
Sorry! Det finns ett till villkor i uppgiften som jag inte la märke till. Jag kommer skapa en ny tråd sen om jag inte kommer vidare.




