Variabelbyte med tanx

Hej!

1)

Måste du använd just $t =\hspace{0.17em}\ln \left(\cos \right(x\left)\right)$ som ditt variabelbyte?

2)

Vad menar du med t1 och t2? Jag hänger inte riktigt med dig där.

3)

Som du redan märkt är detta en generaliserad integral, eftersom din integrand är odefinierad i $x=\frac{\mathrm{\pi }}{2}$. Vet du hur man brukar hantera generaliserade integraler?

Hej

tror du krånglar till det för dig med variabelbyte. Använd regeln ${\int }_{}^{}f\text{'}\left(x\right)/f\left(x\right)dx = \ln \left|f\right(x\left)\right| +C$

så tror jag det faller ut enklare.

Edit: Missade att övre gränsen var 90° och då funkar inte det då cos(90) är 0..

Moffen skrev:

Hej!

1)

Måste du använd just $t =\hspace{0.17em}\ln \left(\cos \right(x\left)\right)$ som ditt variabelbyte?

2)

Vad menar du med t1 och t2? Jag hänger inte riktigt med dig där.

3)

Som du redan märkt är detta en generaliserad integral, eftersom din integrand är odefinierad i $x=\frac{\mathrm{\pi }}{2}$. Vet du hur man brukar hantera generaliserade integraler?

 1) tänkte att det var enklast eftersom dt/dx=-sinx/cosx som sedan kan skrivas om så -dt/dx=sinx/cosx. 

2) Menar att t1 och t2 är gränserna.

3) Ska jag beräkna gränsvärdet av $\frac{lim}{t->\infty }{\int }_0^t-dt$ eller tänker jag fel?

lamayo skrev:

Moffen skrev:

Hej!

1)

Måste du använd just $t =\hspace{0.17em}\ln \left(\cos \right(x\left)\right)$ som ditt variabelbyte?

2)

Vad menar du med t1 och t2? Jag hänger inte riktigt med dig där.

3)

Som du redan märkt är detta en generaliserad integral, eftersom din integrand är odefinierad i $x=\frac{\mathrm{\pi }}{2}$. Vet du hur man brukar hantera generaliserade integraler?

 1) tänkte att det var enklast eftersom dt/dx=-sinx/cosx som sedan kan skrivas om så -dt/dx=sinx/cosx. 

2) Menar att t1 och t2 är gränserna.

3) Ska jag beräkna gränsvärdet av $\frac{lim}{t->\infty }{\int }_0^t-dt$ eller tänker jag fel?

 Precis som CurtJ skriver, så testa istället att använda variabelbytet:

 $$\begin{gathered} u=\cos x \Rightarrow du=-\sin x: \\ {\int }_0^{\frac{\mathrm{\pi }}{2}}\tan xdx=\underset{a\to \infty }{\lim }-{\int }_0^a\frac{du}{u}=... \end{gathered}$$

Du tänker korrekt, men ditt variabelbyte verkar onödigt krångligt om jag får säga det själv, och jag hänger inte med på vad du gör i ditt variabelbyte. 

Integralen för en funktion är ju arean mellan funktionen och x-axeln i det givna intervallet och eftersom tan(pi/2) är odefinierat så undrar jag om din integral har nån lösning. Det testar du ju lätt genom att lösa integralen för någon mindre övre gräns då lösningen är som jag antydde ovan. Ju närmare pi/2 du kommer med övre gränsen desto större blir värdet vilket borde antyda att lösningen är oändligt stor. Rätta mig gärna om jag har fel.

Moffen skrev:

lamayo skrev:

Visa föregående citat

Moffen skrev:

Hej!

1)

Måste du använd just $t =\hspace{0.17em}\ln \left(\cos \right(x\left)\right)$ som ditt variabelbyte?

2)

Vad menar du med t1 och t2? Jag hänger inte riktigt med dig där.

3)

Som du redan märkt är detta en generaliserad integral, eftersom din integrand är odefinierad i $x=\frac{\mathrm{\pi }}{2}$. Vet du hur man brukar hantera generaliserade integraler?

 1) tänkte att det var enklast eftersom dt/dx=-sinx/cosx som sedan kan skrivas om så -dt/dx=sinx/cosx. 

2) Menar att t1 och t2 är gränserna.

3) Ska jag beräkna gränsvärdet av $\frac{lim}{t->\infty }{\int }_0^t-dt$ eller tänker jag fel?

 Precis som CurtJ skriver, så testa istället att använda variabelbytet:

 $$\begin{gathered} u=\cos x \Rightarrow du=-\sin x: \\ {\int }_0^{\frac{\mathrm{\pi }}{2}}\tan xdx=\underset{a\to \infty }{\lim }-{\int }_0^a\frac{du}{u}=... \end{gathered}$$

Du tänker korrekt, men ditt variabelbyte verkar onödigt krångligt om jag får säga det själv, och jag hänger inte med på vad du gör i ditt variabelbyte. 

 jag får att gränsvärdet är 0?

Intressant, visa gärna hur du har gjort så kan vi gå igenom det steg för steg (integralen är divergent!).

lamayo skrev:

 jag får att gränsvärdet är 0?

 Om du plottar funktionen $f(x)=\tan(x)$ från 0 till $\pi/2$ så förstår du varför "arean under kurvan" i det här fallet går mot oändligheten

Men substitutionen är listig och det vore synd att överge den, testa istället att beräkna integralen

$\displaystyle \int_0^{\pi/3} \tan(x)$

Moffen skrev:

Intressant, visa gärna hur du har gjort så kan vi gå igenom det steg för steg (integralen är divergent!).

 har gjort så

Guggle skrev:

lamayo skrev:

 jag får att gränsvärdet är 0?

 Om du plottar funktionen $f(x)=\tan(x)$ från 0 till $\pi/2$ så förstår du varför "arean under kurvan" i det här fallet går mot oändligheten

Men substitutionen är listig och det vore synd att överge den, testa istället att beräkna integralen

$\displaystyle \int_0^{\pi/3} \tan(x)$

 Såg det,

får såhär då: antar bättre svara ln0,5 än att avrunda.

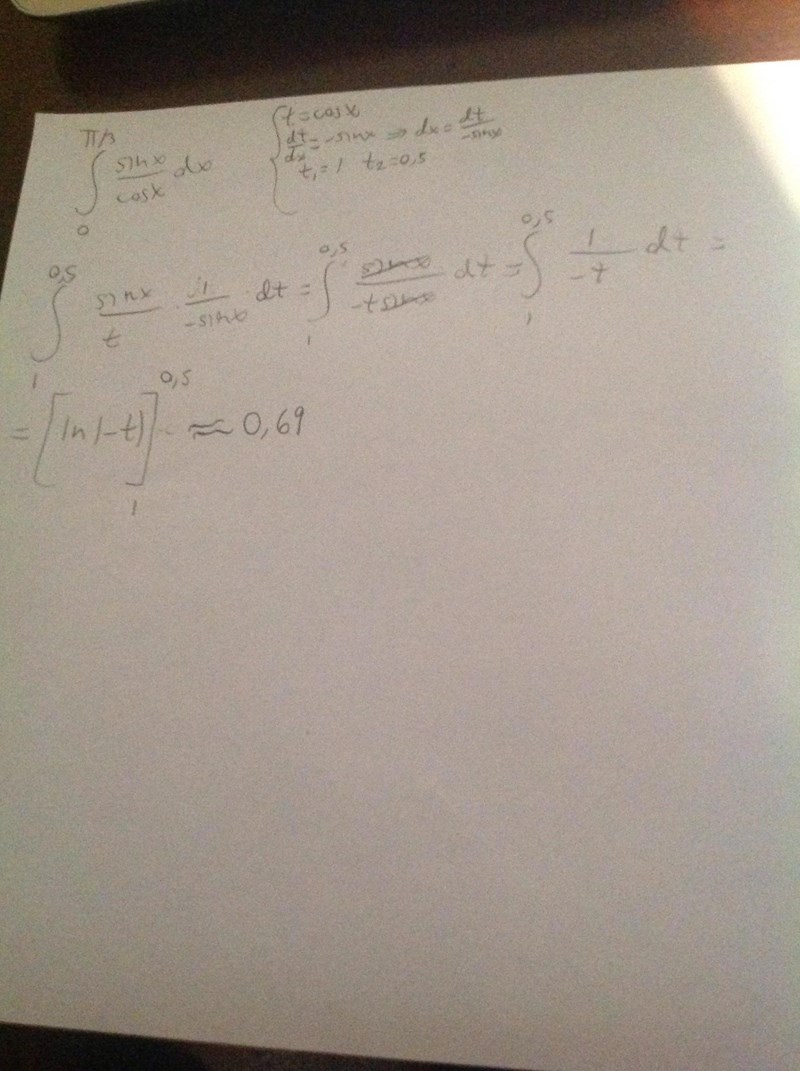
lamayo skrev:

Moffen skrev:

Intressant, visa gärna hur du har gjort så kan vi gå igenom det steg för steg (integralen är divergent!).

 har gjort så

 Det ser bra ut!

Nu är det bara sista delen kvar:

$-{\int }_1^{\infty }\frac{dt}{t}=\underset{a\to \infty }{\lim }-{\int }_1^a\frac{dt}{t}=\underset{a\to \infty }{\lim }-\left[\ln \left|a\right|-\ln \left|1\right|\right]=-\underset{a\to \infty }{\lim }\ln \left(a\right)$

Detta gränsvärde konvergerar ej och därför är integralen divergent.

EDIT: Ser att jag i ett inlägg ovanför har skrivit fel integrationsgränser, men av någon anledning kan jag inte redigera just det inlägget. Det ska iallafall vara 1 som undre integrationsgräns, inte 0.

Moffen skrev:

lamayo skrev:

Visa föregående citat

Moffen skrev:

Intressant, visa gärna hur du har gjort så kan vi gå igenom det steg för steg (integralen är divergent!).

 har gjort så

 Det ser bra ut!

Nu är det bara sista delen kvar:

$-{\int }_1^{\infty }\frac{dt}{t}=\underset{a\to \infty }{\lim }-{\int }_1^a\frac{dt}{t}=\underset{a\to \infty }{\lim }-\left[\ln \left|a\right|-\ln \left|1\right|\right]=-\underset{a\to \infty }{\lim }\ln \left(a\right)$

Detta gränsvärde konvergerar ej och därför är integralen divergent.

 

EDIT: Ser att jag i ett inlägg ovanför har skrivit fel integrationsgränser, men av någon anledning kan jag inte redigera just det inlägget. Det ska iallafall vara 1 som undre integrationsgräns, inte 0.

 Okej, Tack så mycket för hjälpen!

lamayo skrev:

får såhär då: antar bättre svara ln0,5 än att avrunda.

 

Ja, jättebra. Om du vill vara riktigt elegant kan du också använda att $-\ln(0.5)=-\ln(2^{-1})=\ln(2)$.

Alltså får du det vackra och något oväntade

$\displaystyle \int_0^{\pi/3} \tan(x)\,dx=\ln(2)$

Vilket gör åtminstone mig glad när jag ser det :)

Guggle skrev:

lamayo skrev:

får såhär då: antar bättre svara ln0,5 än att avrunda.

 

Ja, jättebra. Om du vill vara riktigt elegant kan du också använda att $-\ln(0.5)=-\ln(2^{-1})=\ln(2)$.

Alltså får du det vackra och något oväntade

$\displaystyle \int_0^{\pi/3} \tan(x)\,dx=\ln(2)$

Vilket gör åtminstone mig glad när jag ser det :)

 Tack så mycket för hjälpen!