Varför tar man (n-2) x 180 i polygoner. Enligt tabellen.

180 kommer från att man måste dela upp det i tranglar, men varför (n-2)?
Om vi har en triangel, dvs. n = 1, har vi tre hörn. Om antalet hörn i en n-hörning ska stämma, måste vi alltså dra bort två hörn. Detta märks tydligast om du delar in några polygoner i trianglar:
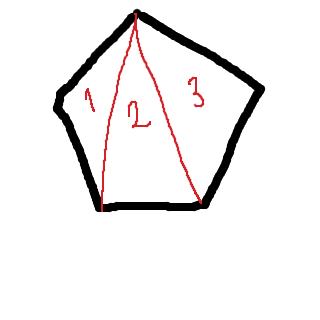
En pentagon ger tre trianglar. Om du lägger på ett hörn (hexagon) tillkommer ännu en rektangel, och om du lägger på ett hörn till, får du en femte triangel. :)
...men varför (n-2)?
Fundera över t.ex. dom två inringade talen i figuren nedan.

Ju men jag ser den numeriska mönstret men det blir bara ett sifferspel om man inte försår bakomliggande principen, det där med triangel exempel, a jag vet inte, det är lite bökigt, jag tänkte jag låter bli att dubbelfråga, men jag kanske måste ändå göra det, vad säger denna inritade triangeln egentligen?
det blir lite som palindrom eller superpalindrom, det finns ett samband, men den säger inte så mycket, man läser bara talen från höger till vänster. Eller ett ambigram.
Så här tänker jag: Detta ser ut att vara en triangel, men i själva verket är det (t ex) en sjuhörning, där 4 av hörnen är 180o vardera. Alltså är vinkelsumman i en sjuhörning 180o +4*180o = 5*180o = (7-2)*180o.




