Varför skriver man allt som en olikhet och hur väljer man oberoende var.?

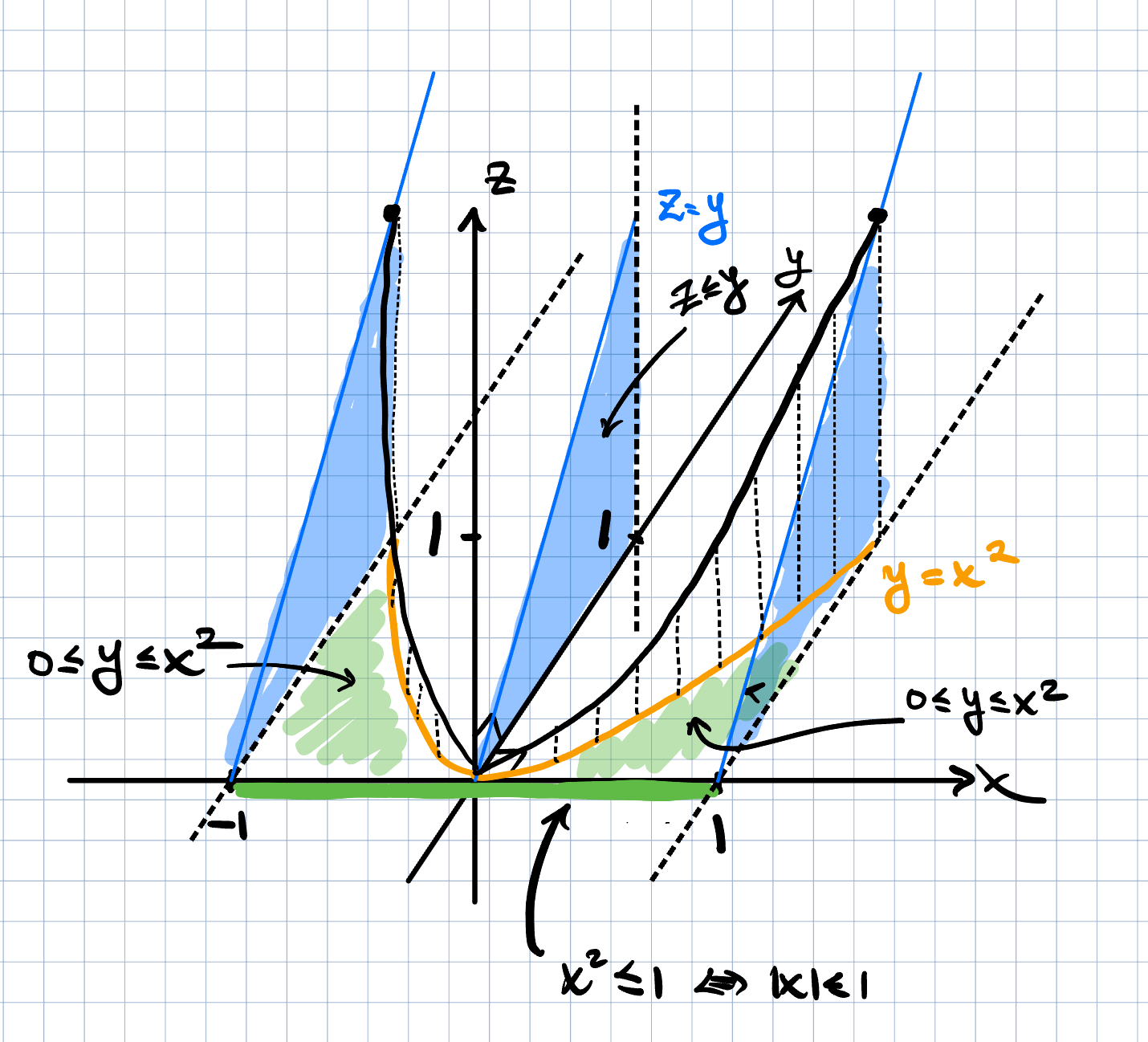
Området är en tredimensionell kropp. Det kräver förstås betydande rutin för att genast se den framför sig (en rutin jag saknar), men jag undrar hur man skulle kunna göra det enklare. Jag ska försöka rita och se vad jag får ut av det.

Frågan blir sedan ska jag integrera … dx dy dz eller i en annan ordning. När jag lyckats rita området kanske det klarnar. CU

Det jag menar är att man t.ex. kan beskriva området som:

$\displaystyle \{ (x,y,z)\in\mathbb{R^3}:-1\le x\le 1,0\le y\le x^2,0\le z \le y\}$

Jag är dock extremt dålig på att se hur man ska välja sin fria variabel och hur man sedan ska välja gränserna för sina resterande, beroende variabler. Nu följer ordningen $dzdydx$ implicit.

Jag kom nog fram till samma som Trinity2. Min bild kommer såklart bli bli legendarisk. 

Vi har ett plan y = z som begränsar uppåt.

Sedan en lodrät parabelyta y = x² som begränsar åt höger.

Och (planen) x = ±1 som begränsar i riktning mot och från betraktaren.

Slutligen planen y = 0 och z = 0 som begränsar åt vänster och nedåt.

Knepigt, men jag störs inte så av det kompakta skrivsättet.

Marilyn skrev:

Jag kom nog fram till samma som Trinity2. Min bild kommer såklart bli bli legendarisk. 

Vi har ett plan y = z som begränsar uppåt.

Sedan en lodrät parabelyta y = x² som begränsar åt höger.

Och (planen) x = ±1 som begränsar i riktning mot och från betraktaren.

Slutligen planen y = 0 och z = 0 som begränsar åt vänster och nedåt.

 

Knepigt, men jag störs inte så av det kompakta skrivsättet.

En fin bild. Här är mitt bidrag till ”Friends of Jackson Pollock”

Tack för era svar!

Jag är dock fortfarande lite förvirrad, särskilt över ditt inlägg #4, @Trinity2. Det känns som att du börjar i "fel ände" eller vad man ska säga. Finns det något sätt att välja sin oberoende variabel först (blev $x$ i vårt fall), och sedan komma fram till resterande gränser? 

naytte skrev:

Tack för era svar!

Jag är dock fortfarande lite förvirrad, särskilt över ditt inlägg #4, @Trinity2. Det känns som att du börjar i "fel ände" eller vad man ska säga. Finns det något sätt att välja sin oberoende variabel först (blev $x$ i vårt fall), och sedan komma fram till resterande gränser? 

Om man märket att integranden blir riktigt svår får man välja en annan riktning. Då kanske man får ett "variabelbidrag" från gränserna som "tillverkar" en inre derivata av integranden och man ps.s. kan finna en primitiv fkn och "stega upp ett steg" i integrationsdjupet.

Färg är Fusk. 

Generellt vill jag ivra för att för att vrida x- och y-axeln litet snett. Då får man fram det tredimensionella djup som min bild så känsligt förmedlar.

naytte skrev:

”Finns det något sätt att välja sin oberoende variabel först (blev x i vårt fall)…”

Nja, det blir ju x sist tycker jag. Men vi kanske tänker lika.

Det jag menar är att jag tycker det är extremt ologiskt att först välja gränserna på $z$ och $y$, och sedan välja gränserna på $x$. Jag tycker det som är så ologiskt med detta är att $z$ och $y$ beror på $x$, så $x$ borde begränsas först. Så som ni verkar tänka är i min hjärna "fel håll".

Marilyn skrev:

Färg är Fusk. 

Generellt vill jag ivra för att för att vrida x- och y-axeln litet snett. Då får man fram det tredimensionella djup som min bild så känsligt förmedlar.

"Colors by Benetton"...

Din bild speglar samtiden så vackert där kontrasterna mellan svart och vitt (öst-väst, nord-syd, x-y, y-z, x-z?) upplöses med ett stilfullt värdegrundsverifierat rutnät och fångar oss alla i en varm omfamning längs y. 

Jag gillar den gamla skolan av "art", när det var svart/vitt och "kopparstick". Man ser sällan dessa illustrationer idag när allt kan göras med dator.

Fast jag lät AI rita

Bara för att förtydliga min fråga: finns det något sätt att komma fram till hur $x$ varierar först, och sedan resterande variabler? Om vi helt från början bestämmer oss för ordningen $dzdydx$.

Eller för att ändra frågan lite: hur skulle det se ut om vi valde $z$ som fri variabel istället? Går det att lirka fram hur den varierar fritt först, och sedan bestämma resterande begränsningar?

Marilyn skrev:

Fast jag lät AI rita

Kan något AI rita vackra bilder (om vi bortser från ADD kreatur).

Här är mitt digitala/manuella försök

Om vi börjar med x så går x från –1 till roten ur y, därefter från roten ur y till 1.

y går från 0 till z och sist går z från 0 till 1.

Tror jag, har inte tänkt jättenoga på det. Det blir två fall i första integrationen, så det känns jobbigare.

Men i vissa uppgifter (kan inte ge exempel) kan byte av integrationsordningen innebära att man slipper en primitiv funktion som kan vara svår eller omöjlig att bestämma.

Trinity2, den var snygg! Jag trodde bara du var poet men du har många konstformer på din palett.

Marilyn skrev:

Trinity2, den var snygg! Jag trodde bara du var poet men du har många konstformer på din palett.

Tack!

"There is no end to my talents"

Som Marilyn skriver kan ibland en "ofullständig" integrand kompletteras med sin inre derivata om gränserna innehåller en lämplig funktion. Då kan man i dessa fall "få in" denna funktion i integranden när man integrerar i en speciell riktning och sedan därifrån lättare finna en primitiv funktion för att sedan gå till nästa variabel. Det är inte helt lätt att ställa upp ett regelverk utan man får se på fall från fall. Det är inget svar som någon vill höra, men det är tyvärr så att 2- och 3-integraler är "knepiga" och likt "pussel" får man vända och vrida på det. Ibland kan man utnytta att någon funktion är udda eller jämtni någon riktning och på så sätt komma vidare.

Jag tittade kort i Persson/Böiers Analys II, men fann inte något liknande område som vi kunde öva mera på. 2- och 3-integraler brukar ställa till det för folk, det är inte helt lätt ibland.

Det kanske kan hjälpa att ta ett exempel där gränserna redan är explicita och försöka göra om det till "kompakt" notation. Låt säga att vi har ett enklare, tvådimensionellt område som ges av:

$0\le x\le 1,0\le y\le x^2$

Hur skulle man skriva om detta på "kompakt form"?

naytte skrev:

Det kanske kan hjälpa att ta ett exempel där gränserna redan är explicita och försöka göra om det till "kompakt" notation. Låt säga att vi har ett enklare, tvådimensionellt område som ges av:

$0\le x\le 1,0\le y\le x^2$

Hur skulle man skriva om detta på "kompakt form"?

Det är inte alltid det går. 1:a kvadraten, x≥0, y≥0 kan inte skrivas mycket "kompaktare" om man inte inte inför en regel att "," = "och" och skriver x,y≥0 men det kan vara lite vanskligt. Matematikprovet har tidvis infört denna typ av "kompakta" former men jag tycker inte de är speciellt lämpliga. De är någon fix idé(?) de har i Göteborg.

Attans.

Får väl helt enkelt be till gud att mina tentafrågor inte kommer på den här otrevliga formen och om det händer får jag väl helt enkelt brösta missade poäng. Det är alldeles för ologiskt för mig, av någon anledning.

Brukar inte ha den här typen av problem i matematiken men just exemplet i #1 stör mig verkligen. Det känns som det borde vara trivialt men något går fel i huvudet.

Försöker mig på en liten sista förklaring i hopp om att det ska hjälpa.

Just i ditt exempel så finns alla 3 variabler x², y och z inom 2 definitiva gränser. Därmed kommer alla dessa variabler sträcka sig inom [0,1]. Notera att det innebär att x sträcker sig inom [-1,1]. Nu är det bara att bestämma vilken som du vill sätta som oberoende (denna kommer få just detta intervall). Därefter bestämmer du de andra utifrån denna.

Anledningen till denna notation är troligen för att man slipper bestämma beroende/oberoende variabler. Istället kan man på en effektivt sätt bestämma deras relation på en enda rad.

Men låt säga då att vi låter $z$ vara vår oberoende variabel i exemplet i #1. Eftersom $z$ sträcker sig fritt över $[0,1]$ har vi:

$0\le z \le 1$

Som nedre gräns för $y$ har vi $0$ (eftersom $z$ börjar på $0$) och som övre gräns $x^2$. För $x^2$ har vi nedre gräns $0$ (eftersom $y$ börjar på $0$) och övre gräns $1$, så $-1 \le x\le 1$... och någonstans har det gått fel för nu har vi två fria variabler.

y kommer begränsas av  $z\le y\le 1$ och x kommer begränsas av $y\le x^2\le 1$.

Alternativt (om vi tar x först): $z<x^2<1$ och $z\le y\le x^2$

Tillägg: 24 mar 2025 11:56

Det du gör fel är att du säger att nedre gränsen för x och y är 0. Det stämmer inte eftersom att de inte får vara mindre än z. Eftersom z är fri kan det vara t.ex. 0.8 och då blir det den undre gränsen för y.

Det du gör fel är att du säger att nedre gränsen för x och y är 0. Det stämmer inte eftersom att de inte får vara mindre än z. Eftersom z är fri kan det vara t.ex. 0.8 och då blir det den undre gränsen för y.

Jo men okej, det köper jag. Nu när jag har sovit på saken är jag med på åtminstone den detaljen.

Men jag förstår inte hur vi kan "hoppa över" $x^2$ i vår olikhetskedja och säga $y \le 1$ istället för $y \le x^2$?

Vi skapar en beroendekedja:

• z är vår oberoende variabel.
• y är beroende av z
• x är beroende av z och y

Vi skulle kunna skriva om usprungsolikheten till $0\le z\le 1, z\le y\le x^2\le 1$, men då har vi kvar samma problem för den andra ekvationen. I den andra ekvationen måste vi nu låta x vara beroende av y eller y beroende av x. Notera att båda fortfarande är beroende av z. Detta ger oss vår beroendekedja.

Jaaaa okej, så vi har en identisk beroendekedja fast med $z$ som nedre gräns, och då måste vi välja nästa "fria" variabel över $[z, 1]$?

Ja precis.

Och anledningen till denna beroendekedja är för att vi ska kunna utföra vår integral.
Eftersom att z är en fri variabel kan vi integrera bort denna. Då kommer övriga variabler tappa z-beroendet. Därmed vill vi att en annan variabel är en fri variabel. Om både x och y beror på varandra kommer ingen av de vara en fri variabel och vi kan därmed inte utföra nästa integral.

I beroendekedjan i #27 kommer vi få följande

• z är en fri variabel som vi integrerar bort. x och y tappar sina z-beroenden
• y blir en fri variabel som vi integrerar bort. x tappar sitt y-beroende
• x är en fri variabel som vi integrerar bort.

Voila! Integralen löst.

Hmm. Jag är inte riktigt med på vad du menar med att vi tappar variabelberoenden. Skulle du kunna skriva upp en itererad integral med dessa gränser fast med "funktionalberoendet" i variablerna? Jag tror det blir tydligare då.

Eller om vi kan utgå ifrån att:

$\displaystyle 0\le z\le y\le x^2\le 1\iff0\le z\;\wedge\; z\le y\;\wedge\; y\le x^2\;\wedge \; x^2\le 1$

Jag tror att det skulle vara lättare att förstå om vi behandlade varje olikhet "individuellt", om det går.

Om vi för enkelhetens skull väljer $x$ som fri variabel så ger olikheten längst till höger:

$-1\le x\le1$

Den andra olikheten ger $y\le x^2$.  Detta ger intervallet:

$y \le x^2$

Den sista två olikheterna tillsammans ger $0 \le z \le y$.

Problemet som kvarstår är intervallet för $y$. Hur ska man motivera att den nedre gränsen är noll? Det är klart att det gäller att $0\le y$, men det är ju INTE samma sak som att $y\in [0, x^2]$. Det är ju tekniskt sett sant att $-20 \le x$ men det innebär ju inte att $x\in [-20, 1]$.

En tanke angående just detta. Är det inte extrmet kass notaton att använda olikheter för att specificera området istället för att faktiskt specificera intervall? Kedjan som gavs i uppgiften var:

$\displaystyle 0\le z\le y \le x^2 \le 1$

Men detta säger inget om över vilka intervall $x,y,z$ sträcker sig över. Det är exakt lika sant att:

$\displaystyle -100\le z\le y\le x^2\le 17$

Olikheten uppfylls för vilka godtyckliga lägre och högre gränser som helst. Det är exakt lika sant. Men det betyder inte att $z\in [-100, 17]$, om $z$ är den fria variabeln.

naytte skrev:

Om vi för enkelhetens skull väljer $x$ som fri variabel så ger olikheten längst till höger:

$-1\le x\le1$

Den andra olikheten ger $y\le x^2$.  Detta ger intervallet:

$y \le x^2$

Den sista två olikheterna tillsammans ger $0 \le z \le y$.

Problemet som kvarstår är intervallet för $y$. Hur ska man motivera att den nedre gränsen är noll? Det är klart att det gäller att $0\le y$, men det är ju INTE samma sak som att $y\in [0, x^2]$. Det är ju tekniskt sett sant att $-20 \le x$ men det innebär ju inte att $x\in [-20, 1]$.

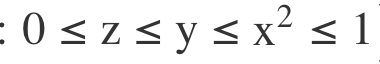
ger att 0≤y.

naytte skrev:

En tanke angående just detta. Är det inte extrmet kass notaton att använda olikheter för att specificera området istället för att faktiskt specificera intervall? Kedjan som gavs i uppgiften var:

$\displaystyle 0\le z\le y \le x^2 \le 1$

Men detta säger inget om över vilka intervall $x,y,z$ sträcker sig över. Det är exakt lika sant att:

$\displaystyle -100\le z\le y\le x^2\le 17$

Olikheten uppfylls för vilka godtyckliga lägre och högre gränser som helst. Det är exakt lika sant. Men det betyder inte att $z\in [-100, 17]$, om $z$ är den fria variabeln.

Här har du utvidgat området. 

Här har du utvidgat området.

Men olikheten jag här där är väl också sann? Det stämmer ju också. Mängden $D$ ges av:

$\displaystyle D:=\{ (x,y,z)\in\mathbb{R^3}:0\le z\le y\le x^2\le 1 \}$

Men detta säger ju ingenting om hur variablerna faktiskt varierar. Det skulle väl lika gärna kunna vara så att $z\in [0.2, y]$ och vi har fortfarande $0 \le z \le y$. Det står inte att "det minsta värdet på $z$ är $0$". Det står bara att "$z$ alltid är större än eller lika med $0$".

Fast då får vi kanske inte med alla punkter i rummet som uppfyller villkoret...

Trinity2 skrev:

naytte skrev:

Om vi för enkelhetens skull väljer $x$ som fri variabel så ger olikheten längst till höger:

$-1\le x\le1$

Den andra olikheten ger $y\le x^2$.  Detta ger intervallet:

$y \le x^2$

Den sista två olikheterna tillsammans ger $0 \le z \le y$.

Problemet som kvarstår är intervallet för $y$. Hur ska man motivera att den nedre gränsen är noll? Det är klart att det gäller att $0\le y$, men det är ju INTE samma sak som att $y\in [0, x^2]$. Det är ju tekniskt sett sant att $-20 \le x$ men det innebär ju inte att $x\in [-20, 1]$.

ger att 0≤y.

Det är detta jag inte förstår. Eller jag fattar men samtidigt inte.

Vi har att $y\le x^2$. Så för ett givet $x$ så ska $y$ vara mindre än $x^2$, men det måste samtidigt vara sant att $z \le y$. Eftersom $z$ som minst kan vara $0$ så måste det minsta $y$:et också vara $0$.

Detta är ju en logisk förklaring som jag kan formulera, men jag förstår ändå inte, tror jag. Det är svårt att förklara men det är skillnad på att förstå och förstå. När man förstår något djupare än bara logiskt så känns det trivialt. Det här känns inte trivialt. Fattar inte hur något så enkelt kan orsaka sådana stora problem.

Nu klickade det nog!

Vi har $y\le x^2$. Om vi stoppar in det minsta värdet på $x^2$ får vi:

$0 \le z \le y \le 0$

Eftersom $0\le y\le 0$ måste $y=0$ och vi har $0\le y\le x^2$

Fattar inte hur något så trivialt kunde vara så svårt att fatta.

Tack för hjälpen!

naytte skrev:

Nu klickade det nog!

Vi har $y\le x^2$. Om vi stoppar in det minsta värdet på $x^2$ får vi:

$0 \le z \le y \le 0$

Eftersom $0\le y\le 0$ måste $y=0$ och vi har $0\le y\le x^2$

Fattar inte hur något så trivialt kunde vara så svårt att fatta.

Tack för hjälpen!

Men vi skulle kunna ha y≤x^2+1≤2 utan att z 'trängs ihop' mellan 2 gränser. Man skall mera tolka 0≤z≤a att z kan anta alla värden i [0,a], även om 0.2≤z är sant för _vissa_ z, men inte alla.