Varför påstår Desmos att det finns två extrempunkter?
Halloj!
Jag sitter med uppgiften nedan:

Det jag tycker är märkligt här är att när jag löser fram extrempunkterna får jag bara en, nämligen en minimipunkt. Wolframalpha verkar hålla med mig:
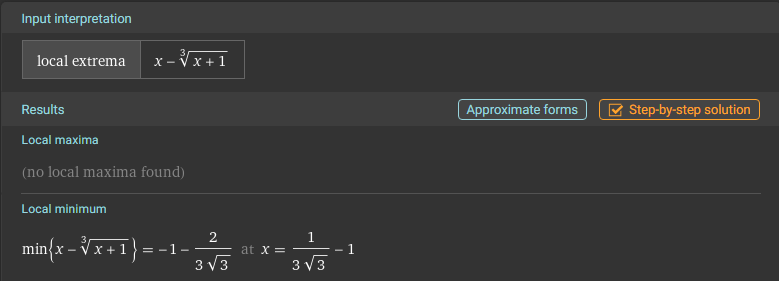
Detta var även det minimum jag erhöll. Men när jag grafar funktionen i Desmos får jag:
Desmos tycker alltså att det finns två extrempunkter. Vem är det som har rätt här? Wolfram och jag eller Desmos?
Generellt så är inte roten ur negativa tal definierat, och wolframalpha antar att x≥-1. Dock så finns t.ex. det reella talet 3√-5 i bemärkelsen att det är den unika reella lösningen på ekvationen x3=-5, nämligen -3√5. Detta går för udda exponenter som i det här fallet. Men om du testar att ändra 3:an till en 4:a i Desmos så borde grafen endast visas för x≥-1.
Vad menar du med att wolframalpha antar att x≥1? Värdet på x för det lokala minimet är ju negativt.
Sorry, ska stå -1, ändrade nu.
Har själv inte så god koll på detta men det verkar bero på vilken tredjerot man tar. Notera skillnaden i dessa två bilder där wolframalpha säger att den använder "principal root" och "real-valued root". Det finns ju tre olika tredjerötter
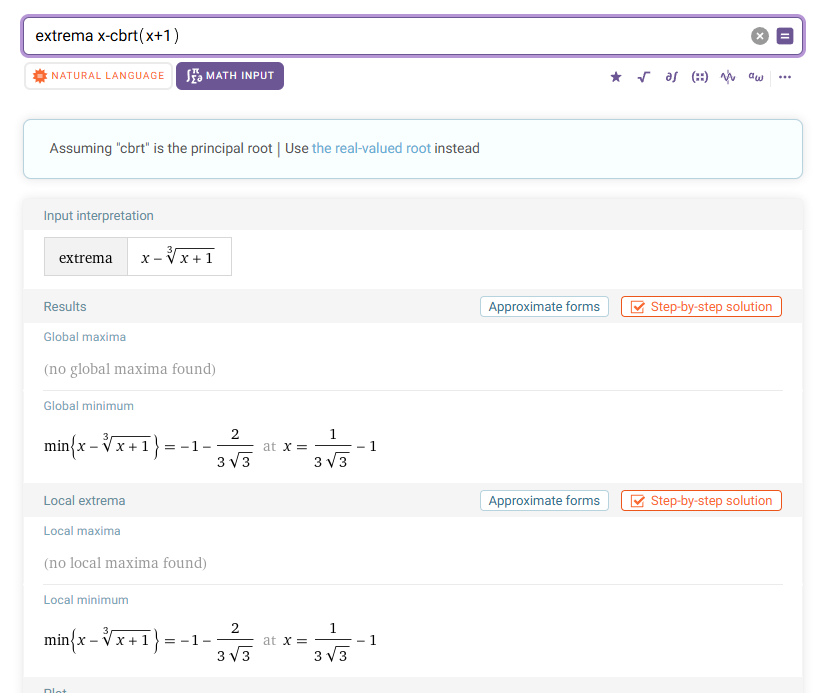
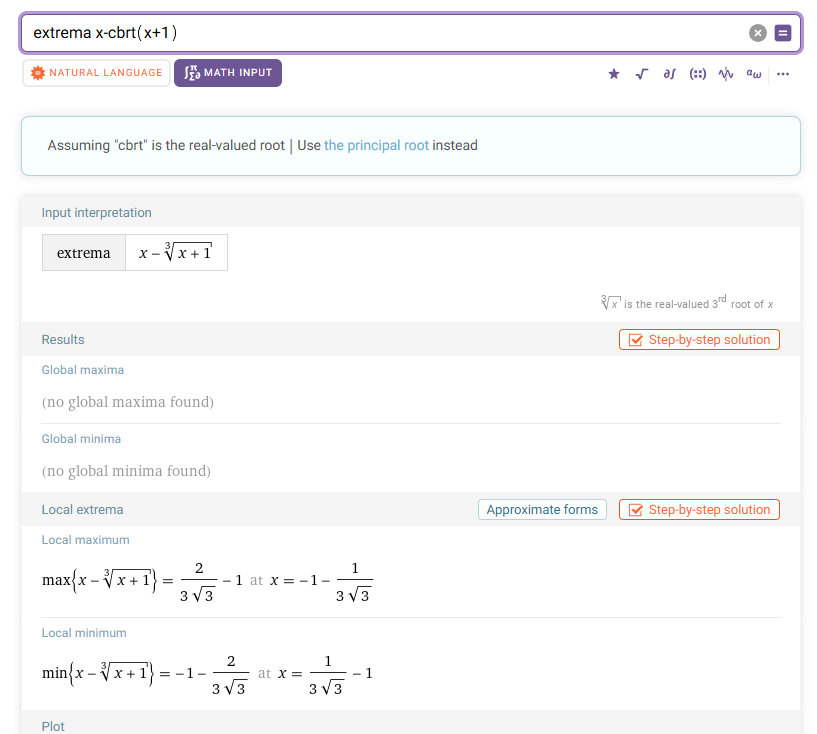
Jag antar desmos alltid väljer det som gör värdet reellt. Men det kanske inte räknas som "samma tredjerot" och då kommer wolframalpha inte visa den som sitt första resultat?
Ah gud vad dum jag är. Jag glömde bara ta ± när jag löste ekvationen (i mitt huvud så var det ^1/3 och inte ^2/3 när jag löste f'(x) = 0)... Herre gud vad jag har fallen off algebraiskt alltså.
Tack för hjälpen!
Det beror helt enkelt på vilken definition av exponentiering man använder. Det vanliga är att man inte tillåter n:te rötter av negativa tal, och det är garanterat så det är tänkt i uppgiften.
Som sagt finns dock t.ex. det reella talet 3√-5 i bemärkelsen att det är den unika lösningen till x3=-5. Det går alltså att definiera n:te rötter ur negativa tal då n är udda, och dessa blir då reella tal. Dock är denna utökade definition inte alltid så bra att använda eftersom potenslagen (ax)y=axy inte gäller. Till exempel: ((-1)2)1/2=11/2=1, men ((-1)2)1/2=(-1)2/2=-1.



