Varför har punkterna samma potential?

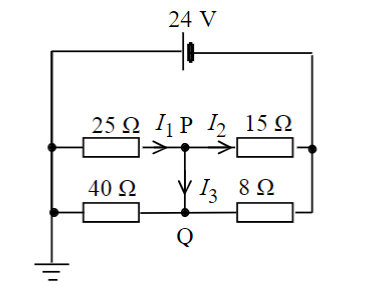
Nej, det beror på att det inte finns någon resistans mellan punkterna. Eftersom U = R•I så blir U = 0 om R = 0.

Av samma anledning har punkterna A och B samma potential:

Så om två punkter är förbundna med en ledare utan motstånd kommer de, oberoende av strömmens riktning, ha samma potential?

naytte skrev:

Så om två punkter är förbundna med en ledare utan motstånd kommer de, oberoende av strömmens riktning, ha samma potential?

Ja det stämmer.

Saknas det inte en ström uppåt också? alltså i ledaren går det en ström I₃ nedåt, men borde det inte gå en I₄ uppåt?

Det behövs inte.

Om uträkningarna visar att I₃ blir negativ så innebär det att strömmen istället går från Q till P.

Hur skulle den kunna bli negativ? Skulle du kunna visa med ett räkneexempel på kretsen?

Det är precis som kaströrelse angående gravitation. Du får fritt ange riktnigen till alla strömmar, men du måste vara konsekvent. Så länge du är konsekvent så gör det ingen skillnad, de kommer få rätt tecken. Ett minustecken betyder att strömmen flödar åt andra hållet.

Samma gäller en spänningskälla. Du får, om du vill, rotera den. Men då får du ta hänsyn till att alla tecken flippas.

Den simpla förklaringen är: 

Om du råkar vända på alla tecken (de är minus istället för plus) så fås:

$-I_1-I_2-I_3-....-I_n=...$, om du nu multiplicerar HL och VL med ett minustecknet så håller fortfarande ekvationen. Den algebraiska summan bryr sig alltså inte vilken riktning du tycker att strömmar och dylikt flödar, men den bryr sig om att du är konsekvent.

Dracaena skrev:

Det är precis som kaströrelse angående gravitation. Du får fritt ange riktnigen till alla strömmar, men du måste vara konsekvent. Så länge du är konsekvent så gör det ingen skillnad, de kommer få rätt tecken. Ett minustecken betyder att strömmen flödar åt andra hållet.

Samma gäller en spänningskälla. Du får, om du vill, rotera den. Men då får du ta hänsyn till att alla tecken flippas.

Den simpla förklaringen är: 

Om du råkar vända på alla tecken (de är minus istället för plus) så fås:

$-I_1-I_2-I_3-....-I_n=...$, om du nu multiplicerar HL och VL med ett minustecknet så håller fortfarande ekvationen. Den algebraiska summan bryr sig alltså inte vilket riktning du tycker att strömma och dylikt flödar, men den bryr sig om att du är konsekvent.

Kruxet i vad jag förstår är varför ingen av strömmen skulle gå uppåt? Om punkterna får samma potential då de förbinds borde väl strömmen inte ha någon "preferens". Regeln med att ström går från hög till låg potential blir väl oanvändbar där? För de sker ju en fördelning av strömmen i både Q och P.

Riktningen av strömmarna är utritade i bilden. Det finns inget som tyder på att den riktningen stämmer överens men det algebraiska tecknet strömmen får.

Som min bild ovan, minustecken betyder att strömmen flödar åt andra hållet från riktningen vi har ritat den eftesrom vi anger vad hög och låg potential blir. Det är av samma aneldning du får, om du vill, ange + och - på dina komponenter, så länge du är konsekvent.

Enklast är så här:

Bestäm dig (nu har de redan gjort de åt dig) vilket håll strömmar ska flöda. Sedan är det bara att räkna. Om du ritade någon ström åt fel håll så ser du det på teckent. 

naytte skrev:

Kruxet i vad jag förstår är varför ingen av strömmen skulle gå uppåt? Om punkterna får samma potential då de förbinds borde väl strömmen inte ha någon "preferens". Regeln med att ström går från hög till låg potential blir väl oanvändbar där? För de sker ju en fördelning av strömmen i både Q och P.

Är du med på att strömmen I i kretsen har den riktning som anges av den röda pilen, dvs från B till A, trots att punkt A och B har samma potential?

Ja.

Bra. Strömmen I har ingen "preferens" mellan A och B, men ändå flyter strömmen från B till A på grund av andra anledningar.

På samma sätt är det med P och Q.

Om dina beräkningar visar att strömmen flyter från P till Q så blir I₃ positiv, om de visar att strömmen istället flyter från Q till P så blir I₃ negativ.

Ja, men strömmen flyter från B till A eftersom den rör sig mot minuspolen på batteriet. Men I P och Q rör sig strömmen mot minuspolen oavsett om den vandrar upp eller ned i ledaren. I P kommer strömmen dela upp sig i två delar. Därför borde den väl dela upp sig i Q också? En ström mot 8 ohms-resistorn samt en ström uppåt mot 15 ohms-resistorn.

Gör så att du inför nya storheter enligt bilden så blir det lättare att prata om strömmarna.

Du har rätt i att både P och Q är punkter där strömmen antingen delar upp sig i två delar eller slås ihop från två delar till en.

Med storheter enligt bilden så har vi för punkterna P och Q att

• I₁ = I₂+I₃, dvs I₁ delar upp sig i två delströmmar I₂ och I₃
• I₃+I₄ = I₅, dvs de två delströmmarna I₃ och I₄ slås ihop till I₅

Dessutom gäller det att

• I = I₁+I₄, dvs I delar upp sig o de två delströmmarna I₁ och I₄
• I₂+I₅ = I, dvs de två delströmmarna I₂ och I₅ slås ihop till I

Fråga: Är du med på ovanstående?

Vi kan beräkna I genom U = R•I, där U är 24 V och R är kretsens totala resistans. Vi kan sedan beräkna storleken av övriga delströmmar.

Om det då visar sig att en eller flera av delströmmarna får negativt tecken så innebär det bara att de strömmarna flyter i motsatt riktning gentemot hur pilarna visar.

Se även Dracaenas svar #8.