Varför ges centripetalkraften av mgtan(alfa)

Här är en ful bild som illustrerar kraftsituationen: 

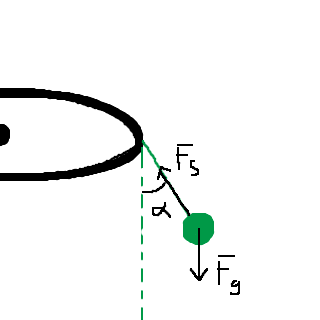där F_S är spännkraften i snöret (den har säkert något korrekt och fint namn jag glömt, men motkraften i linan i alla fall 😅). 

Om vi "drar ut" linan lite längre får vi följande situation: 

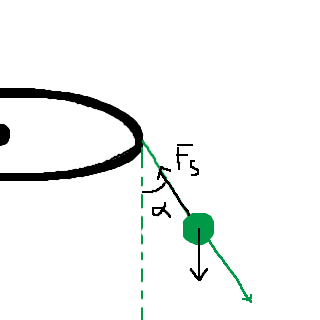
Vilken blir vinkeln mellan linan och den förlängda linan? Hur kan vi uttrycka centripetalkraften med hjälp av denna vinkel? :)

Smutstvätt skrev:

Här är en ful bild som illustrerar kraftsituationen: 

där F_S är spännkraften i snöret (den har säkert något korrekt och fint namn jag glömt, men motkraften i linan i alla fall 😅). 

Om vi "drar ut" linan lite längre får vi följande situation: 

Vilken blir vinkeln mellan linan och den förlängda linan? Hur kan vi uttrycka centripetalkraften med hjälp av denna vinkel? :)

Det var en väldigt bra bild :). Justeja, linan kommer ju behöva dels motverka tyngdkraften från gungan så att den inte faller mot marken och dels dra in den mot centrum så gungan inte försvinner ut mot horisonten. Linans spännkraft vertikalt är Fcos(alfa) = mg. Och dess spännkraft horisontellt är Fsin(alfa). Vinkeln kommer öka av någon anledning så att den inte drar mer än den behöver i vertikal riktning när centripetalkraften ökar. Hmm... det är intressant. Som ni märker är jag ute på lite outforskat territorium här när jag tänker. Vinkeln kan aldrig bli pi/2 eftersom då finns det ingen vertikal kraft. Vi har iallafall sambandet Fcos(alfa) = mg och Fsin(alfa) = mw^2r. Men kommer inte vidare i tankarna härifrån. Tips?

Ser nu hur man får centripetalkraften:

$$\begin{gathered} F=\frac{mg}{cos\left(\alpha \right)} \\ F\sin \left(\alpha \right)=mg\tan \left(\alpha \right) \end{gathered}$$

Jag är inte säker på om du känner dig klar med denna tråd?

Om inte: Jag tänker att resonemanget kring varför centripetalkraften är $F_C=mg\tan{(\alpha)}$ är enklare än så. Vi komposantuppdelar spännkraften i tråden till att vara centripetalkraften och normalkraften till tyngdkraften.

 $\tan \left(\alpha \right)$ är då centripetalkraften (riktad inåt, dvs. åt vänster) dividerat med tyngdkraften, dvs. $\tan \left(\alpha \right)=\frac{F_C}{mg}$, och då kan vi lösa ut $F_C$. 

Smutstvätt skrev:

Jag är inte säker på om du känner dig klar med denna tråd?

Om inte: Jag tänker att resonemanget kring varför centripetalkraften är $F_C=mg\tan{(\alpha)}$ är enklare än så. Vi komposantuppdelar spännkraften i tråden till att vara centripetalkraften och normalkraften till tyngdkraften.

 $\tan \left(\alpha \right)$ är då centripetalkraften (riktad inåt, dvs. åt vänster) dividerat med tyngdkraften, dvs. $\tan \left(\alpha \right)=\frac{F_C}{mg}$, och då kan vi lösa ut $F_C$. 

Hur kommer det sig egentligen att man kan division av två krafter som pekar i två vinkelräta mot varandra riktningar kan ge tangens av en vinkel. Är det bara krafterna som styr i vilka horisontella och vertikala riktningar linan är mot vertikalen?

Det är egentligen bara storleken av krafterna vi tittar på. Ska vi vara ordentliga ska vi egentligen skriva att $\tan \left(\alpha \right)=\frac{\left|F_C\right|}{m\left|g\right|}$. :)

Dualitetsförhållandet skrev:

Smutstvätt skrev:

Jag är inte säker på om du känner dig klar med denna tråd?

Om inte: Jag tänker att resonemanget kring varför centripetalkraften är $F_C=mg\tan{(\alpha)}$ är enklare än så. Vi komposantuppdelar spännkraften i tråden till att vara centripetalkraften och normalkraften till tyngdkraften.

 $\tan \left(\alpha \right)$ är då centripetalkraften (riktad inåt, dvs. åt vänster) dividerat med tyngdkraften, dvs. $\tan \left(\alpha \right)=\frac{F_C}{mg}$, och då kan vi lösa ut $F_C$. 

Hur kommer det sig egentligen att man kan division av två krafter som pekar i två vinkelräta mot varandra riktningar kan ge tangens av en vinkel. Är det bara krafterna som styr i vilka horisontella och vertikala riktningar linan är mot vertikalen?

Jag har bara slarvläst de frågor som du ställt tidigare i tråden, så jag kanske svarar på helt fel fråga, men jag tar risken... Jag undrar om inte den fråga som du formulerat ovanför, är själva nyckelfrågan. "Är det bara krafterna som styr i vilka horisontella och vertikala riktningar linan är mot vertikalen?". Ja, så är det. Eller kanske snarare tvärtom, den vinkel som linan har, avslöjar de enda riktningar som krafterna som verkar på föremålet kan ha.  

Tänk dig att du håller ett föremål i en lina. Du kommer bara att kunna påverka föremålet med en kraft längs linan. Det innebär att de enda krafter som kan verka på karusellstolen är snörkraften och tyngdkraften.

Eftersom stolens acceleration i y-led är noll, så _måste_ snörkraftens y-komposant vara lika stor som mg. Att jämviktsvillkoret är uppfyllt i y-led sätter villkoret på hur stor snörkraften måste vara. Vilket ger att x-komposanten av snörkraften då måste bli mgtanalpha. Och kraftresultanten i x-led måste ge centripetalkraften eftersom det är en cirkelrörelse.

JohanF skrev:

Dualitetsförhållandet skrev:

Visa föregående citat

Smutstvätt skrev:

Jag är inte säker på om du känner dig klar med denna tråd?

Om inte: Jag tänker att resonemanget kring varför centripetalkraften är $F_C=mg\tan{(\alpha)}$ är enklare än så. Vi komposantuppdelar spännkraften i tråden till att vara centripetalkraften och normalkraften till tyngdkraften.

 $\tan \left(\alpha \right)$ är då centripetalkraften (riktad inåt, dvs. åt vänster) dividerat med tyngdkraften, dvs. $\tan \left(\alpha \right)=\frac{F_C}{mg}$, och då kan vi lösa ut $F_C$. 

Hur kommer det sig egentligen att man kan division av två krafter som pekar i två vinkelräta mot varandra riktningar kan ge tangens av en vinkel. Är det bara krafterna som styr i vilka horisontella och vertikala riktningar linan är mot vertikalen?

Jag har bara slarvläst de frågor som du ställt tidigare i tråden, så jag kanske svarar på helt fel fråga, men jag tar risken... Jag undrar om inte den fråga som du formulerat ovanför, är själva nyckelfrågan. "Är det bara krafterna som styr i vilka horisontella och vertikala riktningar linan är mot vertikalen?". Ja, så är det. Eller kanske snarare tvärtom, den vinkel som linan har, avslöjar de enda riktningar som krafterna som verkar på föremålet kan ha.  

Tänk dig att du håller ett föremål i en lina. Du kommer bara att kunna påverka föremålet med en kraft längs linan. Det innebär att de enda krafter som kan verka på karusellstolen är snörkraften och tyngdkraften.

Eftersom stolens acceleration i y-led är noll, så _måste_ snörkraftens y-komposant vara lika stor som mg. Att jämviktsvillkoret är uppfyllt i y-led sätter villkoret på hur stor snörkraften måste vara. Vilket ger att x-komposanten av snörkraften då måste bli mgtanalpha. Och kraftresultanten i x-led måste ge centripetalkraften eftersom det är en cirkelrörelse.

Läste nu genom denna tråd igen, förstår inte hur du kommer fram till att x-komposanten av snörkraften måste bli mgtanalpha

Krafterna som verkar på gungan är tyngdkraften och snörkraften.

Summering av krafternas komposanter i y-led, och sätt lika med noll, eftersom accelerationen i y-led är noll:

$F_s\cos \alpha -mg=0 \left(1\right)$

Summering av krafternas komposanter i x-led, och sätt lika med centripetalkraften, eftersom det är cirkelformad rörelse i "x-planet":

$F_s\sin \alpha =F_c \left(2\right)$

Från (1) fås att $F_S=\frac{mg}{\cos \alpha }$

insätts i (2):

$$\begin{gathered} \frac{mg}{\cos \alpha }·\sin \alpha =F_c \iff \\ {F}_c=mg\tan \alpha \end{gathered}$$

Och eftersom $F_c$är just snörkraftens komposant i x-led, se (2), så är snörkraftens komposant i x-led: $mg\tan \alpha$

Smutstvätt skrev:

Här är en ful bild som illustrerar kraftsituationen: 

där F_S är spännkraften i snöret (den har säkert något korrekt och fint namn jag glömt, men motkraften i linan i alla fall 😅). 

Om vi "drar ut" linan lite längre får vi följande situation: 

Vilken blir vinkeln mellan linan och den förlängda linan? Hur kan vi uttrycka centripetalkraften med hjälp av denna vinkel? :)

Har det varit en bild här? Jag ser ingen bild.

Laguna skrev:

Smutstvätt skrev:

Här är en ful bild som illustrerar kraftsituationen: 

där F_S är spännkraften i snöret (den har säkert något korrekt och fint namn jag glömt, men motkraften i linan i alla fall 😅). 

Om vi "drar ut" linan lite längre får vi följande situation: 

Vilken blir vinkeln mellan linan och den förlängda linan? Hur kan vi uttrycka centripetalkraften med hjälp av denna vinkel? :)

Har det varit en bild här? Jag ser ingen bild.

Det är något tjall med bilderna. Jag har sett att de funnits, men nu ser jag dem inte. 

Hmmm, jag kan se bilderna, men det verkar inte som att de syns om en använder chrome som webbläsare. :s

$\mathrm{Men} \mathrm{de} \mathrm{är} \mathrm{inte} \mathrm{särskilt} \mathrm{vackra}, \mathrm{så} \mathrm{ni} \mathrm{missar} \mathrm{inget} 😅$

Jo, nu ser jag dem i Safari. 

Det var lite obegripligt utan dem.

Ja, så måste det hänga ihop!!! Jag brukar köra omväxlande Safari och Chrom beroende på enhet.

Ja, jo det blir inte så mycket kvar att gå på utan bilderna. Jag vet inte varför de inte syns i chrome, men jag har haft problem att lägga in bilder från den hemsidan när jag använt chrome, så det kanske är något som inte matchar där. 

JohanF skrev:

Krafterna som verkar på gungan är tyngdkraften och snörkraften.

 

Summering av krafternas komposanter i y-led, och sätt lika med noll, eftersom accelerationen i y-led är noll:

$F_s\cos \alpha -mg=0 \left(1\right)$

Summering av krafternas komposanter i x-led, och sätt lika med centripetalkraften, eftersom det är cirkelformad rörelse i "x-planet":

$F_s\sin \alpha =F_c \left(2\right)$

Från (1) fås att $F_S=\frac{mg}{\cos \alpha }$

insätts i (2):

$$\begin{gathered} \frac{mg}{\cos \alpha }·\sin \alpha =F_c \iff \\ {F}_c=mg\tan \alpha \end{gathered}$$

Och eftersom $F_c$är just snörkraftens komposant i x-led, se (2), så är snörkraftens komposant i x-led: $mg\tan \alpha$

Rent algebraiskt förstår jag det. Men inte intuititvt. Saker jag inte förstår intuitivt brukar jag glömma bort. Så skulle gärna vilja ha en intuitiv förklaring till att centripetalkraften är mgtanalpha