Varför gäller ej två fall av sinussatsen här?
Hej!
Sitter på uppgift 4231 i Matematik 5000 3c.
Uppgiften lyder såhär:
" Beräkna sidan AC samt vinklarna B och C i triangeln ABC om A = 40 grader AB = 36 cm och BC = 50 cm "
Jag gör såhär: sin C = sin40*36/50
C = sin^-1(sin40*36/50) = 27.568 grader
B = 180 - ( 40 + 27.568) = 112.43 grader
AC = 50 * sin112.43/sin40 = 71.9cm
h = 71.9*sin40 = 46.22 cm
Alltså gäller 46.22<BC<71.9. Därför bör ju två trianglar finnas. En med vinkeln B = 112.43 och en med B = 180 - 112.3 = 67.7 grader
Dock säger facit att svaret är B = 112.43 och C = 27.568 med AC = 71.9.
Hur kommer det sig?
Och sedan, en annan generell fråga: Ifall en triangel har två katetrar ( plural? ) som uppfyller villkoren h<k<motstående katet, säger man då att det finns 3 trianglar för de givna måtten?
Tack!
h som du beräknar är höjden ( den rätvinkliga mot C) i triangeln med sidan AB som bas.
Det rätvinkliga hörnet ligger bortanför B.
Om du lägger B i den punkten är ju varken AB=36 eller BC=50(BC=46,22).
Rita en figur.
Massa skrev:h som du beräknar är höjden ( den rätvinkliga mot C) i triangeln med sidan AB som bas.
Det rätvinkliga hörnet ligger bortanför B.
Om du lägger B i den punkten är ju varken AB=36 eller BC=50(BC=46,22).
Rita en figur.
Hej,
Tänkte inte på att det spelar någon roll ifall man beräknar h på AC eller BC, men nu när jag tänker på det så förstår jag att det inte blir så rätt haha.
Däremot så blir höjden ungefär densamma i just detta fallet, dvs omkring 46.22 ( med min felaktiga metod med AC som hypotenusa och AB som bas blir höjden ca 46.217, med BC som hypotenusa så blir det 46.216 ) Därför bör ju fortfarande villkoret h<BC<AC gälla, och därmed två vinklar på B, eller?
Tack!
Det är bara om man har en rätvinklig triangel man kan tala om hypotenusa och katet. I alla andra trianglar heter det bara sidor.
Smaragdalena skrev:Det är bara om man har en rätvinklig triangel man kan tala omhypotenusa och katet. I alla andra trianglar heter det bara sidor.
Aha. När jag sa hypotenusa syftade jag på den sida i triangeln som hade blivit hypotenusan till höjden när jag gjorde beräkningen, eftersom jag " bildar " en rätvinklig triangel med höjden som rätvinklig längd gentemot basen AB.
Hpakuten skrev:Smaragdalena skrev:Det är bara om man har en rätvinklig triangel man kan tala omhypotenusa och katet. I alla andra trianglar heter det bara sidor.
Aha. När jag sa hypotenusa syftade jag på den sida i triangeln som hade blivit hypotenusan till höjden när jag gjorde beräkningen, eftersom jag " bildar " en rätvinklig triangel med höjden som rätvinklig längd gentemot basen AB.
Det är nästan omöjligt att förstå vad du menar, när du inte ritar en bild som visar det.
Smaragdalena skrev:Hpakuten skrev:Smaragdalena skrev:Det är bara om man har en rätvinklig triangel man kan tala omhypotenusa och katet. I alla andra trianglar heter det bara sidor.
Aha. När jag sa hypotenusa syftade jag på den sida i triangeln som hade blivit hypotenusan till höjden när jag gjorde beräkningen, eftersom jag " bildar " en rätvinklig triangel med höjden som rätvinklig längd gentemot basen AB.
Det är nästan omöjligt att förstå vad du menar, när du inte ritar en bild som visar det.
Hej! Ursäkta för mitt sena svar, inte hunnit sätta mig ned och kolla på detta sedan jag postade tråden!
Jag gjorde en figur där jag förklarar hur jag tänker här: https://gyazo.com/02d6d4b3d17dd690e2610e92ab101bbb
Jag hann dock tänka lite mer på det medans jag ritade upp figuren och jag TROR jag kom fram till varför jag har fel. Jag tänkte att jag kanske kunde förklara hur jag tänker så kan du avgöra ifall det ligger något vett i vad jag säger haha.
För att illustrera min poäng ritar jag en ny triangel: https://gyazo.com/62badad586f26d10be8d69bfd95b40f2
Så när vi talar om två fall av sinussatsen så är det inte bara beroende på om sidan vi ska rita är större än höjden och mindre än sidan som är närliggande den givna vinkeln, utan också vilken information vi får given av uppgiften. Två fall gäller ifall den motstående sidan är mindre än sidan som är närliggande till den givna vinkeln, och ifall basen ej är given. Om jag ritar två fall när basen är given hade jag ändrat på triangelns mått, och därför hade det andra fallet inte uppfyllt kraven som är givna av uppgiften.
Tänker jag rätt? Svamlar jag?
Tack!
Här  och här
och här 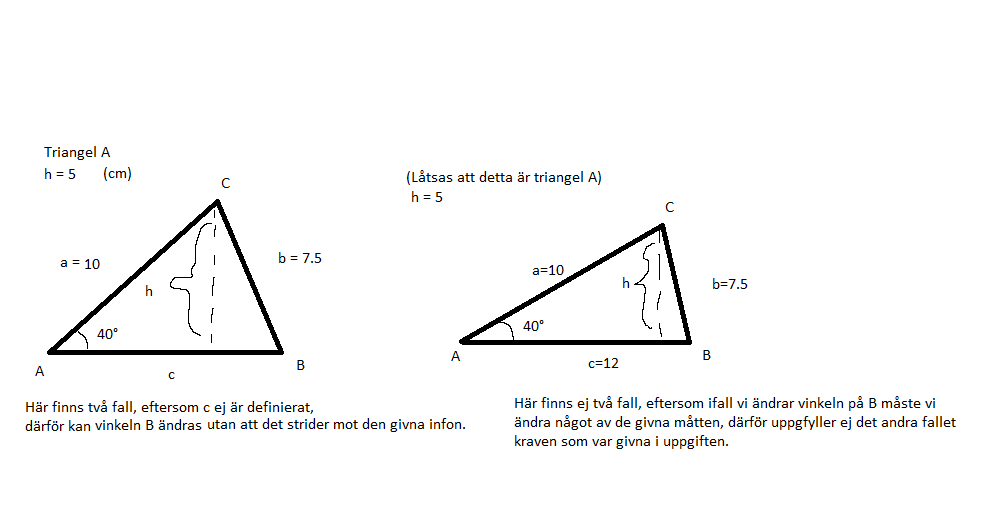 är de båda bilderna från Hpakutens inlägg. Här är en länk till hur man lägger upp bilder i sitt inlägg.
är de båda bilderna från Hpakutens inlägg. Här är en länk till hur man lägger upp bilder i sitt inlägg.
Hpakuten skrev:Alltså gäller 46.22<BC<71.9.
Nej. BC = 50 cm som givet i uppgiften.
Därför bör ju två trianglar finnas. En med vinkeln B = 112.43 och en med B = 180 - 112.3 = 67.7 grader
Kolla här:
Om du gör en triangel med sidorna 3.6, 5 och ena vinkeln 40 grader är den entydigt bestämd.
Du har inte lyckats presentera hur det på något vis kan finnas två olika trianglar där A = 40°, AB = 36 cm och BC = 50 cm.
Ebola skrev:Hpakuten skrev:Alltså gäller 46.22<BC<71.9.
Nej. BC = 50 cm som givet i uppgiften.
Därför bör ju två trianglar finnas. En med vinkeln B = 112.43 och en med B = 180 - 112.3 = 67.7 grader
Kolla här:
Om du gör en triangel med sidorna 3.6, 5 och ena vinkeln 40 grader är den entydigt bestämd.
Du har inte lyckats presentera hur det på något vis kan finnas två olika trianglar där A = 40°, AB = 36 cm och BC = 50 cm.
Hej!

Innan sidan med uppgiften ovan stod dessa villkoren, så när jag skrev min fråga var det dessa jag tänkte på. Jag tänkte då att BC i min triangel motsvarar a, och eftersom bc>h men bc<ac, där ac motsvarar b i villkoren ovan, så bör det finnas två trianglar i uppgiften. Jag tror dock jag förstår varför jag har fel nu haha.
Edit2: Tänker på villkoret i mitten då, där det står h<a<b
Problemet är att AB är given som 36 cm. Hade den inte varit det hade du haft två möjliga trianglar.
Ebola skrev:Problemet är att AB är given som 36 cm. Hade den inte varit det hade du haft två möjliga trianglar.
Okok, det var det jag misstänkte! Jag tänkte inte på att man ska se till så den andra triangeln inte strider mot måtten man får i uppgiften. Förstår nu, tror jag haha. Tack för all hjälp!



