Varför finns inget elektriskt fält i laddade/laddningsförskjutna objekt?

Hej!

Det enda jag förstår är att det i laddade objekt är en jämn utspridning av elektroner på ytan. Detta ger mig bilden av att det endast kommer vara avsaknad av kraft av elektriskt fält i mitten av alla elektroner då alla elektrostatiska krafter skulle ta ut varandra, men avsaknaden av elektriskt fält gäller hela inre delen av kroppen?

Om objektet är ett ledande klot så sprids laddningen jämnt på ytan, eftersom laddningarna vill vara så långt ifrån varandra som möjligt. Fältet inuti ett sådant klot är noll, inte lätt att förklara varför, men det beror på att det inte finns någon laddning inuti klotet. Jag tror inte resonemanget kan överföras till elektronens dimensioner. Dels vet jag inte om elektronen är sfärisk, dels så har elektronen en enda elementarladdning, som det blir knepigt att fördela jämnt över elektronens yta. Kort sagt - dessa modeller duger inte för att förklara dessa egenskaper hos elektronen , utan man måste använda kvantteorier. Tror jag.

Sedan har jag bara hittat förklaringen att symmetrin i en kropp på något sätt leder till att man ska räkna distans i coulombs formel från centrumet, men jag förstår inte riktigt varför :(

Det stämmer, delvis. Kroppen måste vara ett klot (så att det blir sfärisk symmetri) med jämn laddningsfördelning (tex om klotet är ledande). Det är inte så lätt att förklara på ett enkelt sätt, men det beror på att det elektriska fältet utanför en sådan kropp ser likadant ut som om man antog att samma laddning fanns i en punktladdning i dess centrum. 

För laddningsförskjutna kroppar åker elektroner mot riktningen av elektriska fältet som påverkar kroppen, vilket inom kroppen innebär att det bildas ett elektiskt fält som går åt det andra hållet, det blir då ett kraftfält riktat åt elektronerna som förflyttat sig, som då jämnar ut det yttre kraftfältet???

Jag förstår inte riktigt din fråga. Kan du förklara mer?

JohanF skrev:

Hej!

Det enda jag förstår är att det i laddade objekt är en jämn utspridning av elektroner på ytan. Detta ger mig bilden av att det endast kommer vara avsaknad av kraft av elektriskt fält i mitten av alla elektroner då alla elektrostatiska krafter skulle ta ut varandra, men avsaknaden av elektriskt fält gäller hela inre delen av kroppen?

Om objektet är ett ledande klot så sprids laddningen jämnt på ytan, eftersom laddningarna vill vara så långt ifrån varandra som möjligt. Fältet inuti ett sådant klot är noll, inte lätt att förklara varför, men det beror på att det inte finns någon laddning inuti klotet. Jag tror inte resonemanget kan överföras till elektronens dimensioner. Dels vet jag inte om elektronen är sfärisk, dels så har elektronen en enda elementarladdning, som det blir knepigt att fördela jämnt över elektronens yta. Kort sagt - dessa modeller duger inte för att förklara dessa egenskaper hos elektronen , utan man måste använda kvantteorier. Tror jag.

Sedan har jag bara hittat förklaringen att symmetrin i en kropp på något sätt leder till att man ska räkna distans i coulombs formel från centrumet, men jag förstår inte riktigt varför :(

Det stämmer, delvis. Kroppen måste vara ett klot (så att det blir sfärisk symmetri) med jämn laddningsfördelning (tex om klotet är ledande). Det är inte så lätt att förklara på ett enkelt sätt, men det beror på att det elektriska fältet utanför en sådan kropp ser likadant ut som om man antog att samma laddning fanns i en punktladdning i dess centrum. 

För laddningsförskjutna kroppar åker elektroner mot riktningen av elektriska fältet som påverkar kroppen, vilket inom kroppen innebär att det bildas ett elektiskt fält som går åt det andra hållet, det blir då ett kraftfält riktat åt elektronerna som förflyttat sig, som då jämnar ut det yttre kraftfältet???

Jag förstår inte riktigt din fråga. Kan du förklara mer?

Verkar som de första två frågorna blir svåra att svara på? Antar att jag inte behöver kunna göra det i fysik 1 då iallafall :]

På tredje frågan undrade jag att varför precis som i laddade objekt, inte finns ett elektriskt fält inuti en ledare som då ligger i ett elektriskt fält och blir påverkad av influens? Min antagelse är då att elektronerna rör sig på ett sätt som skapar ett elektriskt fält inom ledaren som går i jämvikt med det yttre elektriska fältet? Lite såhär: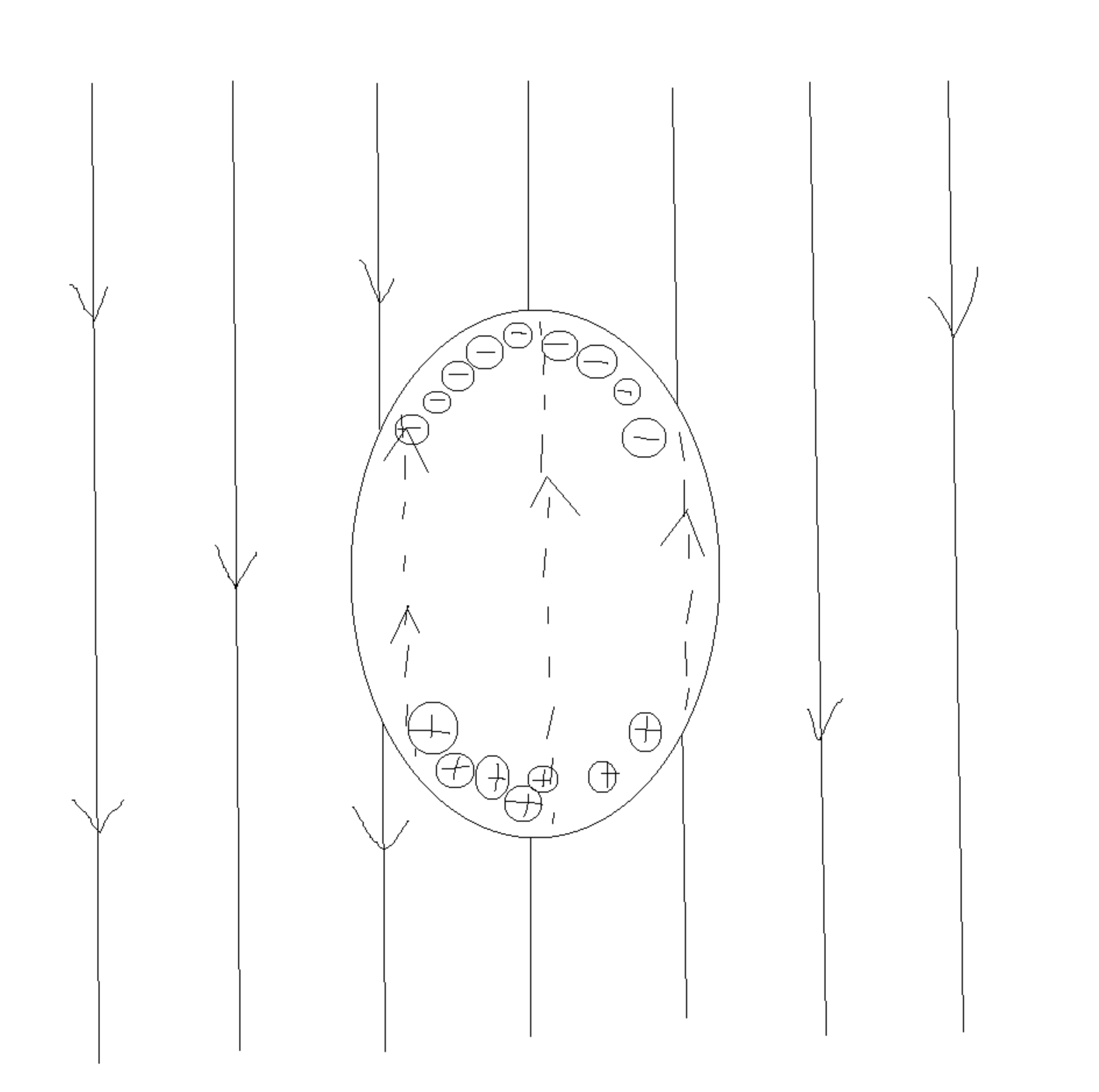

Verkar som de första två frågorna blir svåra att svara på? Antar att jag inte behöver kunna göra det i fysik 1 då iallafall :]

Du kan med gott samvete skippa förklaringen i fysik1. Du måste bara acceptera att det är så. En sådan fråga skulle eventuellt kunna komma på en tentamen i elektromagnetism på universitetsnivå där man först lärt sig Maxwell's ekvationer grundligt (som beskriver hur elektromagnetiska fält beter sig), detta är hans första ekvation.

På tredje frågan

Jaha, det var så du menade! Om jag förstår dig rätt så tror jag att du har helt rätt. I såna här lägen så är det bra att titta på en sak i taget, då ser man lättare vad som är orsak och vad som är konsekvens. Och sedan skilja på det yttre pålagda fältet (dina raka streck utanför ledaren), och det fält som orsakas av att laddningarna förskjuts. Precis som du förklarar.

Vi utgår från din bild. Jag tycker det är lite enklare att tänka i krafter som tar ut varandra i jämvikt, än att fält ska ta ut varandra (men det blir samma sak).

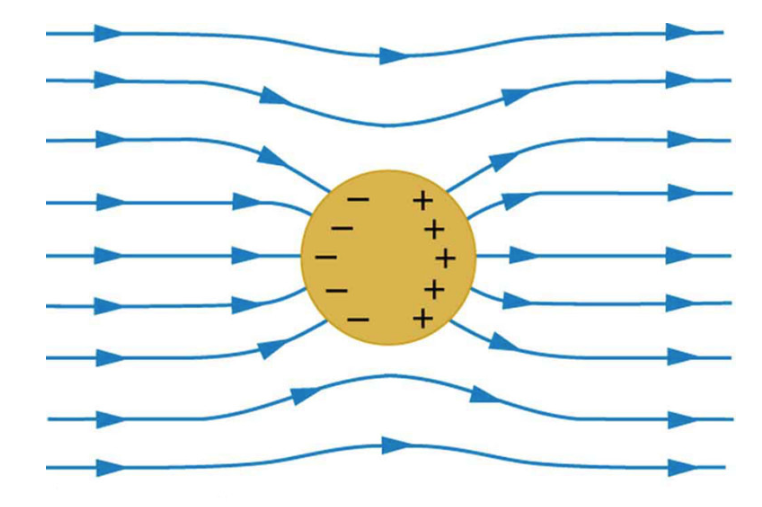
De positiva laddningarna påverkas av en kraft nedåt i bilden ifrån det yttre elektriska fältet, och drar dem mot "väggen" på ledaren. De negativa laddningarna dras uppåt åt motsatt håll. Laddningarna kommer att stanna i ett jämviktsläge där kraften åt ena hållet pga det yttre fältet, uppvägs av coulombkrafterna från de laddningar som dragits isär. Fältet kommer då att utsläckas inuti ledaren (om det finns tillräckligt många fria laddningsbärare därinne). Det som kan tilläggas till din bild att fältet utanför ledare kommer att påverkas lite också, eftersom fältlinjerna utanför ledaren måste ansluta till ledare vinkelrätt mot ledarens yta, vilket man kan tänka sig genom att ifall fältlinjerna inte hade gjort det så skulle laddningsbärarna vid ledarytan inte vara i kraftjämvikt, och förskjutas tills de kom i jämvikt, och därmed få fältlinjerna att ansluta vinkelrätt.

JohanF skrev:

Verkar som de första två frågorna blir svåra att svara på? Antar att jag inte behöver kunna göra det i fysik 1 då iallafall :]

Du kan med gott samvete skippa förklaringen i fysik1. Du måste bara acceptera att det är så. En sådan fråga skulle eventuellt kunna komma på en tentamen i elektromagnetism på universitetsnivå där man först lärt sig Maxwell's ekvationer grundligt (som beskriver hur elektromagnetiska fält beter sig), detta är hans första ekvation.

På tredje frågan

Jaha, det var så du menade! Om jag förstår dig rätt så tror jag att du har helt rätt. I såna här lägen så är det bra att titta på en sak i taget, då ser man lättare vad som är orsak och vad som är konsekvens. Och sedan skilja på det yttre pålagda fältet (dina raka streck utanför ledaren), och det fält som orsakas av att laddningarna förskjuts. Precis som du förklarar.

Vi utgår från din bild. Jag tycker det är lite enklare att tänka i krafter som tar ut varandra i jämvikt, än att fält ska ta ut varandra (men det blir samma sak).

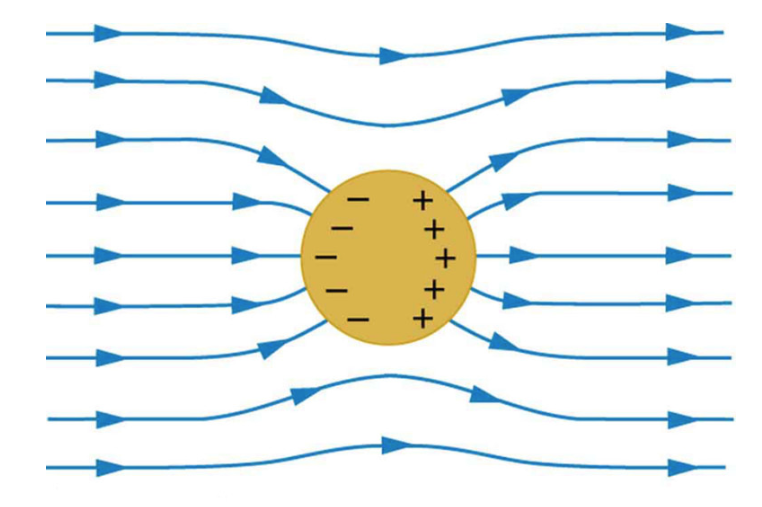
De positiva laddningarna påverkas av en kraft nedåt i bilden ifrån det yttre elektriska fältet, och drar dem mot "väggen" på ledaren. De negativa laddningarna dras uppåt åt motsatt håll. Laddningarna kommer att stanna i ett jämviktsläge där kraften åt ena hållet pga det yttre fältet, uppvägs av coulombkrafterna från de laddningar som dragits isär. Fältet kommer då att utsläckas inuti ledaren (om det finns tillräckligt många fria laddningsbärare därinne). Det som kan tilläggas till din bild att fältet utanför ledare kommer att påverkas lite också, eftersom fältlinjerna utanför ledaren måste ansluta till ledare vinkelrätt mot ledarens yta, vilket man kan tänka sig genom att ifall fältlinjerna inte hade gjort det så skulle laddningsbärarna vid ledarytan inte vara i kraftjämvikt, och förskjutas tills de kom i jämvikt, och därmed få fältlinjerna att ansluta vinkelrätt.

  

Tack så mycket för svaret!!! Tror jag förstår det som behövs nu iallafall :)