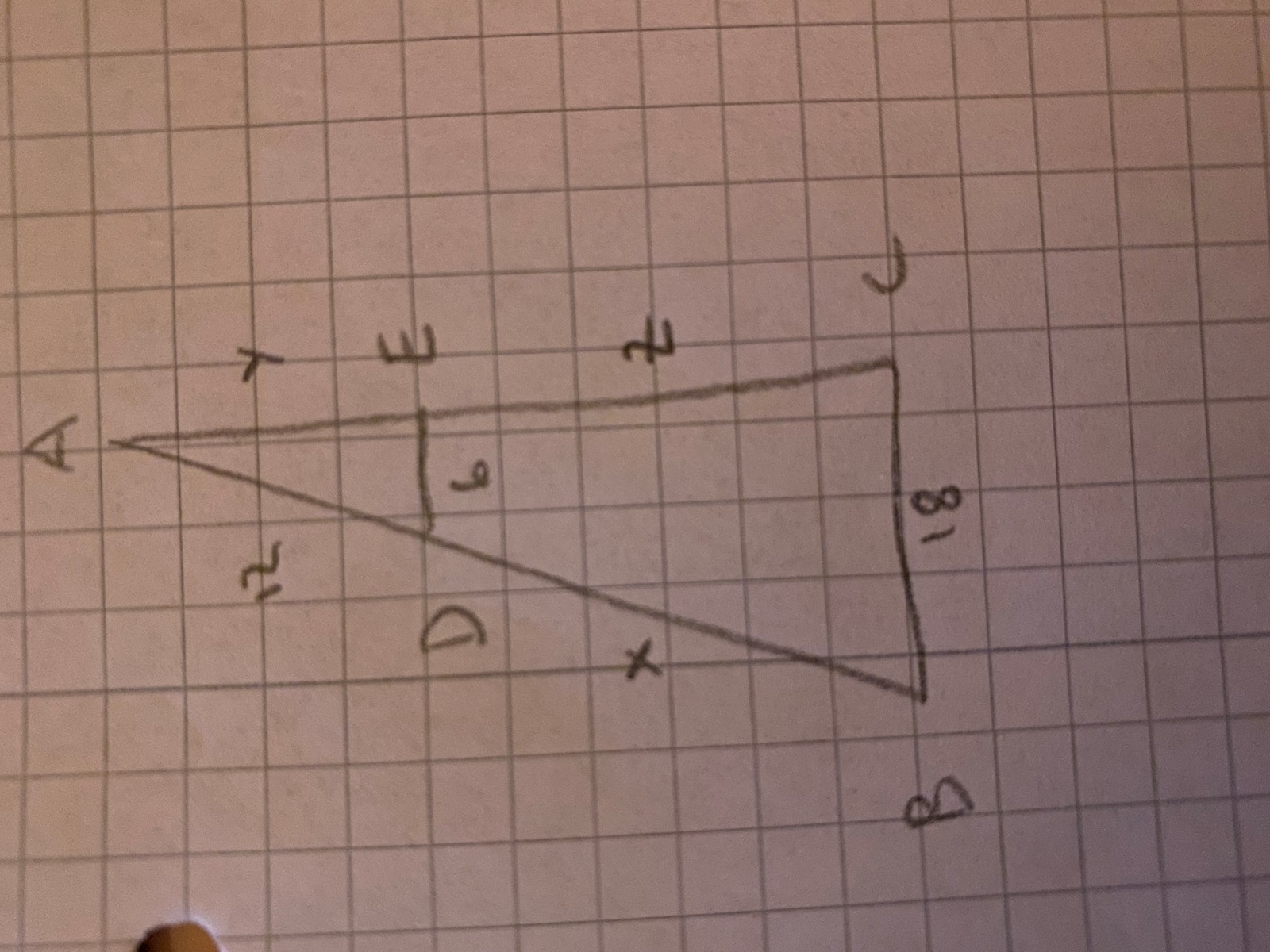Varför får jag ut ett ungefärligt tal, vart räknar jag/tänker jag fel?
Hej,
Håller på med en uppgift b), svaret jag får känns fel & tror det beror på att jag räknat fel på någon sida. För att kunna visa b) uppgiften måste jag gå igenom a) för de hänger ihop.
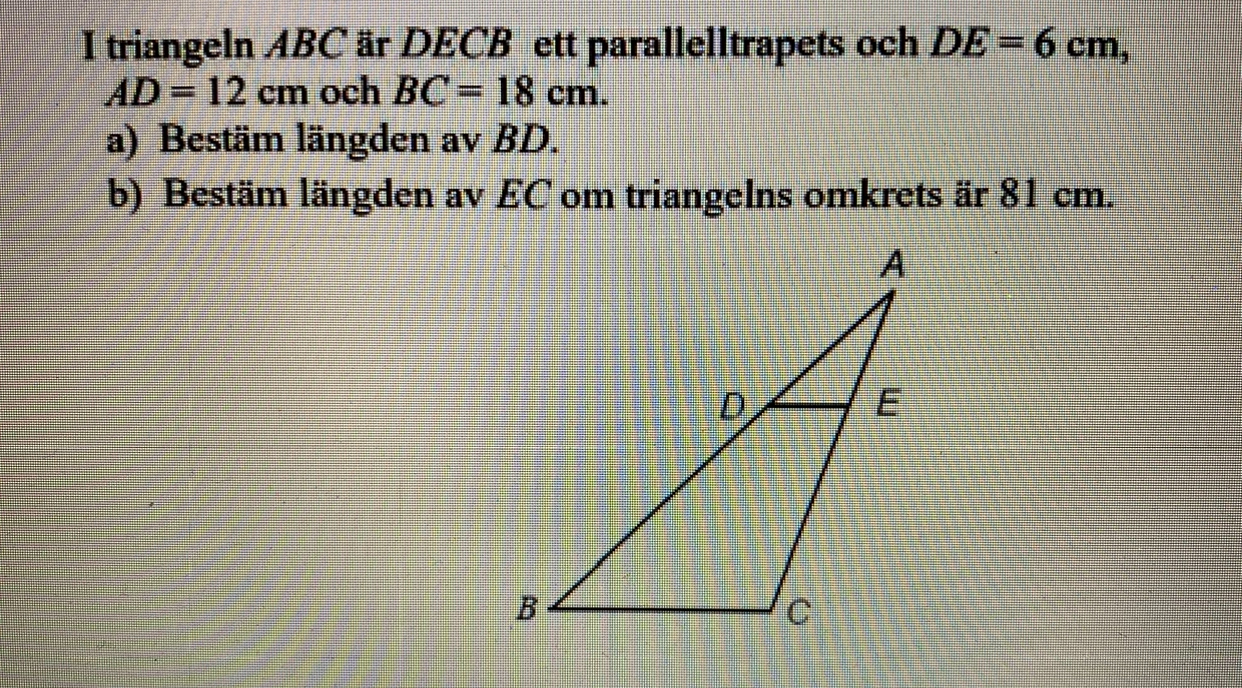
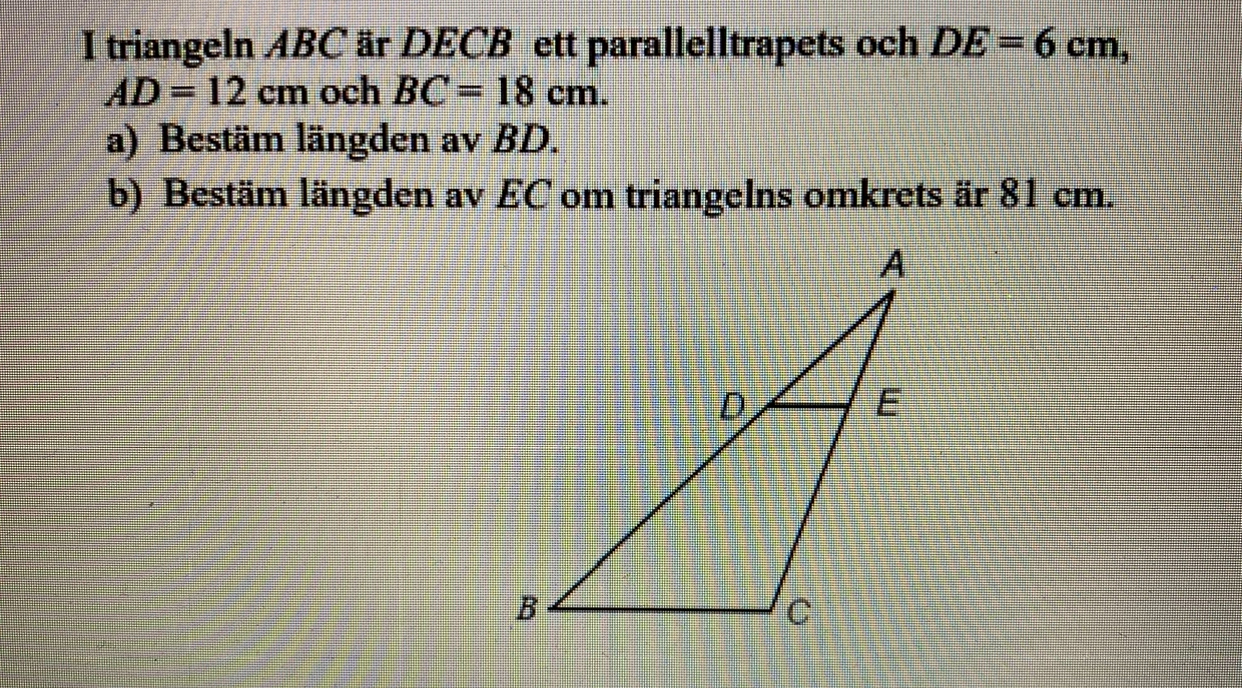
Uppgiften är:
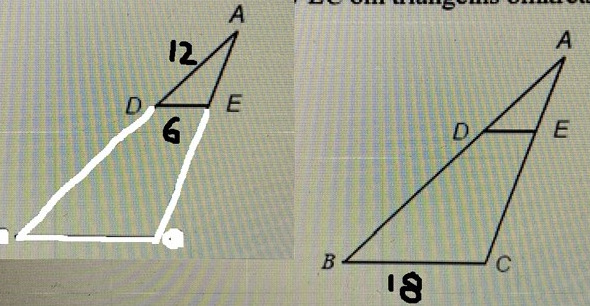
min triangel:
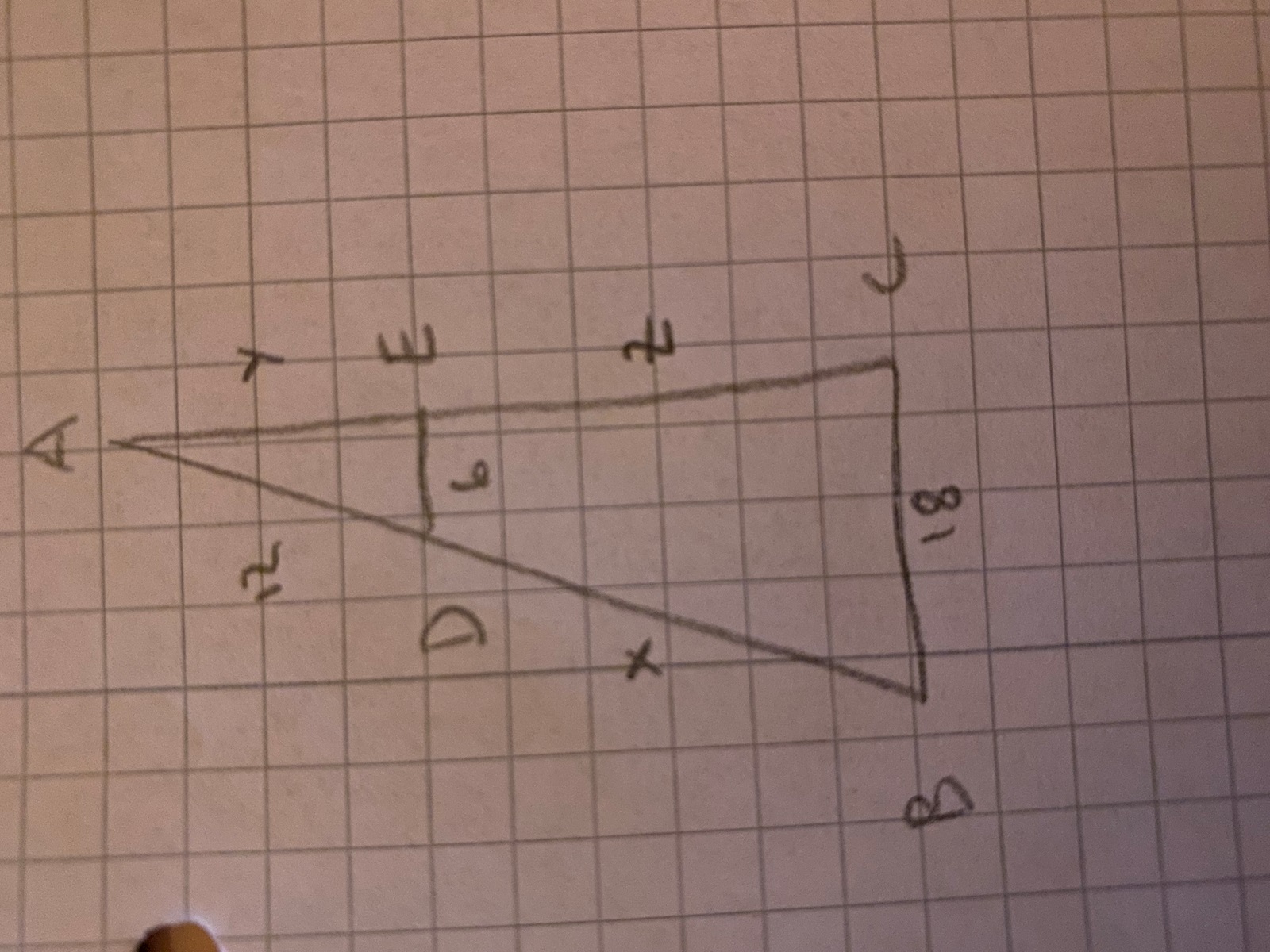
På a) uppgiften tänkte jag:
6/18=12/x Fick fram ett svar som vart BD=36
på b) uppgiften tänkte jag att jag tar:
12^2 + 6^2 = y^2
för att sedan räkna ihop sidorna & ta den summan & dra av från 81 för att sedan se vad jag får kvar & då skulle de bli EC sidan.
när jag tog:
12^2 + 6^2 = y^2
fick jag ett ungefärligt tal så avrunda det till 13 (& de känns fel)
tog hur som alla sidor:
12+36+18+13 = 79
81-79= 2
& det känns fel!
Naturens skrev:Hej,
Håller på med en uppgift b), svaret jag får känns fel & tror det beror på att jag räknat fel på någon sida. För att kunna visa b) uppgiften måste jag gå igenom a) för de hänger ihop.
Uppgiften är:
min triangel:
På a) uppgiften tänkte jag:
6/18=12/x Fick fram ett svar som vart BD=36
på b) uppgiften tänkte jag att jag tar:
12^2 + 6^2 = y^2
för att sedan räkna ihop sidorna & ta den summan & dra av från 81 för att sedan se vad jag får kvar & då skulle de bli EC sidan.
när jag tog:
12^2 + 6^2 = y^2
fick jag ett ungefärligt tal så avrunda det till 13 (& de känns fel)
tog hur som alla sidor:
12+36+18+13 = 79
81-79= 2
& det känns fel!
Längden av BD är ett heltal. Det kanske är enklare om man placerar de båda likformiga trianglarna bredvid varandra, och markerar det man vet:
Samma tankefel som i frågan jag svarade på tidigare ikväll. Kika igenom likformighet igen: https://www.matteboken.se/lektioner/skolar-9/geometri/likformighet
AB=12+x
Okej, tack för svaren, men jag förstår inte vart är det jag gör fel? Jag gick in på länken och läste, men liksom jag förstår inte, jag gör ju så?
a) Bestäm längden av BD.
Jag tar ju 6/18 = 12/x (detta för att få fram längden BD ?) Är det fel tänkt här? eller har jag räknat fel kanske? kan visa hur jag räknat och kommit fram till att BD blir 36?
Vidare på b) tittar jag på den "lilla" triangeln och har sidorna 12 och 6 och jag gör då så här:
12^2 + 6^2 = y^2 och y sidan är då AE sidan. Det är alltså denna sida som blir ett avrundat tal för mig?
***
vänta.. lite... nu.. är det här jag gör fel..
på a) ska det vara: 6/18 = 12/12+x ?
Naturens skrev:vänta.. lite... nu.. är det här jag gör fel..
på a) ska det vara: 6/18 = 12/12+x ?
Där har du det!
Lika sidor i trianglarna har samma förhållanden/proportioner.
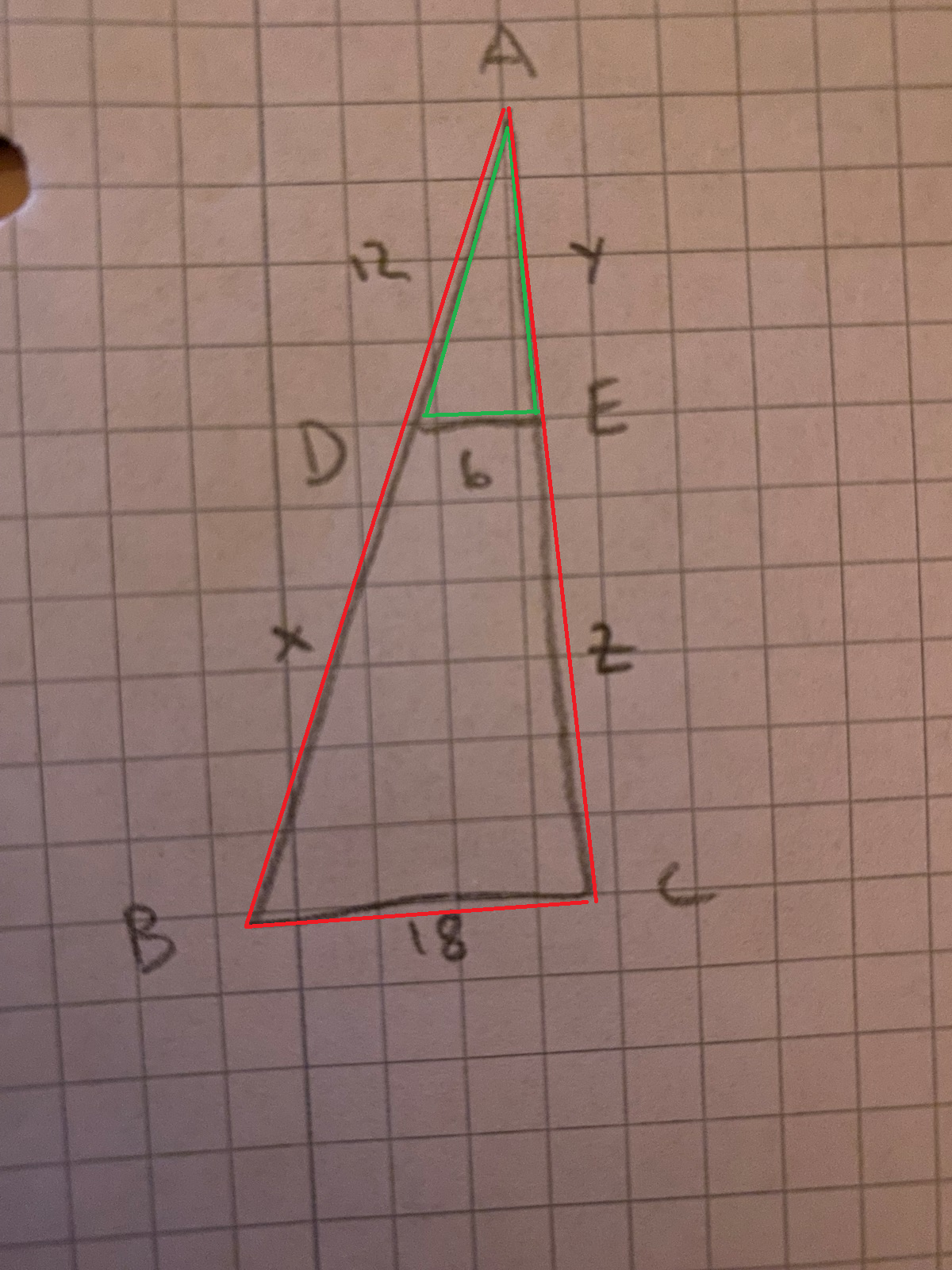
Basen på gröna (=6) förhåller sig till basen på röda (=18), som vänstra benet på gröna (=12) till vänstra på röda (=12+x):
Superenkel högstadiematte, men så lätt att göra fel. Så bra att kunna och väldigt användbart.
Bara att lösa för x.
Tack.
Men om BD= 24 (svaret jag fick när jag räkna fram 6/18=12/12+x) så ändrar det ju inte sidan AC(y)? dvs mitt fel i a) ändra inte decimaltalet jag får fram i b) uppgiften? dvs om jag vill få fram AE så tar jag 12^2+6^2=y^2 och de blir ju ett decimaltal ? dvs ca 13
och 24+12+18+ca 13 blir 67, (så ja här vart de en annan siffra dvs 67 istället för de jag fick fram först)
och 81-67 blir 14, så EC blir ca 14 cm, & jag måste ju skriva ca 14 för jag har ju ett ca 13 som sträckan AE blir?
Så mitt fel i a) uppgiften hjälpte ju inte med decimaltalet jag får fram genom att använda pythagoras sats
Jag tänker att pythagoras är de bästa alternativet att använda för att få fram y sidan?
Pythagoras fungerar bara på rätvinkliga trianglar. Inte här!
Däremot har du precis räknat ut x, så i och med det har du omkretsen av den stora triangeln (från uppgiften) + basen + vänstra benet. Då kan du räkna ut längden av det högra benet. Sedan blir det likformighet igen, fast nu skall du beräkna det du benämnt y.
jaha okej, men om BD har en ekvation som är: 6/18=12/12+x
så kan ju y inte ha en ekvation som är: 6/18= y/y-z utan tänker att jag typ får göra: 6/18=12/y för att lösa ut y ?
och när jag har y löst,
så adderar jag alla sidor och de jag får över blir EC ?
***
Alltså 81 (som är omkretsen) - vad de 4 sidorna blir adderat ihop. Tänker jag
Nej, likformighet fungerar bara för motsvarande sidor:
Det finns inget som säger att:
Allt handlar om att trianglarna är precis lika i sin form, men att den ena är en förstoring av den andra.
Nu har du i stora triangeln:
- BC=18 (från uppgiften)
- AB=12+x=12+24=36 (uträknat)
ABC:s omkrets =81 (från uppgiften). Det ger: AC=81-18-36=27
Nu har du höger ben i stora triangeln AC=27.
Du söker y och likformigheten ger dig:
jahaa.. okej! TACK!
men fråga..
AC=27 och AC är hela höger ben.
När jag ställer upp ekvationen: y/AC = AD/AB så blir AC som är 27 för hela benet, de måste väl bli -y alltså:
y/AC= AD/AB. blir. y/y-27 = 12/12+24 (dvs 36) ?
Titta på din uppställning.
I nämnarna har du längden av de långa benen. De vet du vad de är, 27 resp. 36.
I täljarna har du längden av de korta benen. Det ena är y och det andra är 12.
okej, tack.
Jag gjorde så här:
y/27=12/36
y=9
18+36+9=63
81-63=18
EC=18
Verkar rimligt! Tjusigt!
Likformighet återkommer överallt, så bra att kunna. Fast pythagoras är jätteanvändbart inom geometri, så är det enbart för rätvinkliga trianglar.
Tack för all hjälp.
Ska försöka komma ihåg det i framtida uppgifter.