Varför får jag en negativ massa?
Eftersom systemet är i vila är kraftsumman noll. Således gäller att . Dessutom vet vi att volymen i formeln för lyftkraft kan skrivas om med hjälp av aluminiums densitet:
Således går allt att skriva upp på följande sätt:
När man löser denna ekvation får man dock en negativ massa, så någonting med uppställningen stämmer uppenbarligen inte. Hjälp skulle uppskattas.
Om du ritar ut krafterna, med tydliga riktningar, blir det nog rätt.
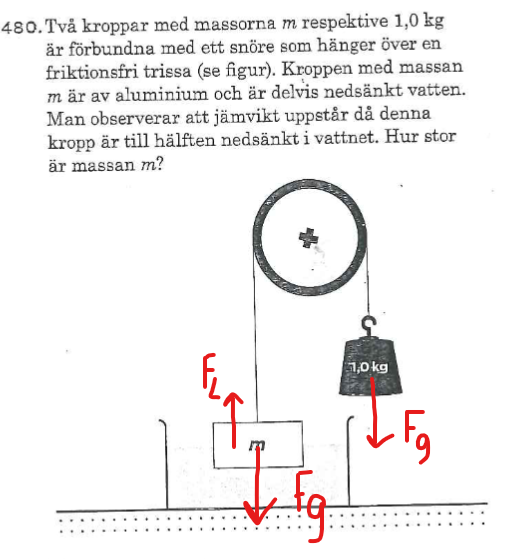 Det var så här jag tänkte krafterna när jag skrev min lösning. Är det inte rätt? Jag ignrorerade spännkraften eftersom det är en intern kraft som inte påverkar.
Det var så här jag tänkte krafterna när jag skrev min lösning. Är det inte rätt? Jag ignrorerade spännkraften eftersom det är en intern kraft som inte påverkar.
naytte skrev:
Jag ignrorerade spännkraften eftersom det är en intern kraft som inte påverkar.
Jodå.
Frilägg aluminiumkroppen i vattnet.
Jag förstår ju att spännkraften påverkar i avseendet att den drar i aluminiumbiten. Men den borde väl inte påverka om man tittar på hela systemet eftersom systemet påverkas av en exakt lika stor, motriktad spännkraft?
naytte skrev:Jag förstår ju att spännkraften påverkar i avseendet att den drar i aluminiumbiten. Men den borde väl inte påverka om man tittar på hela systemet eftersom systemet påverkas av en exakt lika stor, motriktad spännkraft?
Är det samma sak om tyngden står på aluminiumbiten, menar du?
Jag insåg att min ena Fg var riktad åt fel håll i mina beräkningar! Nu ställde jag upp det så här:
och det gav rätt svar. Mitt tankefel först var att båda gravitationskraftena verkade åt samma håll men det gör de ju såklart inte.
Pieter Kuiper skrev:naytte skrev:Jag förstår ju att spännkraften påverkar i avseendet att den drar i aluminiumbiten. Men den borde väl inte påverka om man tittar på hela systemet eftersom systemet påverkas av en exakt lika stor, motriktad spännkraft?
Är det samma sak om tyngden står på aluminiumbiten, menar du?
Det jag menade var att om man beaktar spännkraftena tar de ut varandra ändå om man tittar på hela systemet (jag definierar 1 kg viktens rörelseriktning som positiv):
Tillägg: 4 maj 2023 12:37
Stämmer inte det resonemanget?
Bumpar tidigt för det är kursprov imorgon. Stämmer det resonemanget med att man kan strunta i spännkrafterna?
Trissan är upphängd så du måste räkna med krafterna på den också om du ska räkna "på hela systemet". Annars är det inte i jämvikt.
Men som princip ska du snitta och frilägga aluminiumkroppen. På den verkar spännkraften i linan , och . Det blir enklast så.



