Varför får jag bara med halva lösningsmängden?
Jag har försökt lösa ekvationen , men av någon anledning får jag bara med två av de fem lösningar som finns när jag dubbelkollar med wolframalpha. Min metod går ut på att göra omskrivningen: och sedan para ihop varje möjlig omskrivning och lösa fyra ekvationer:
Då får man två dubblettlösningar, dvs. endast två lösningar totalt. Dessa stämmer enligt wolfram, men där listas tre lösningar till, som inte erhålls när man löser ekvationen så här?
Varifrån kommer resten av lösningarna?
Jag gör så här:
(1)
och
(2)
(1) ger
(2) ger
Vilka lösningar får du och vilka har facit?
De lösningarna du får får jag också. Men wolfram får tre till:
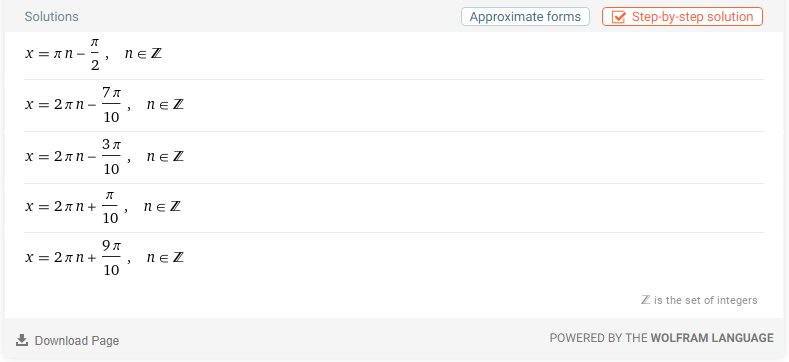
Det är nog samma lösningsmängd. Prova att stoppa in n = 1, 2, osv.
Om vi byter ut vårt n mot 5n, 5n+1, 5n+2, 5n+3 och 5n+4 borde man få facits svar.
Men varför listar de fem lösningar istället för två när två räcker för att beskriva varje möjlig lösning?
Hur Wolfram gör vet jag inte, men du kanske kan se hur den räknar om du trycker på Step-by-Step solution.
Det kan vara bra att ange allting med periodiciteten 2 pi, så kan man se alla lösningarna i enhetscirkeln, men med den metod vi använder så blir det förvisso ett extra steg.
En anledning till som kan finnas att inte behålla den ursprungliga lösningen utan bearbeta den så att man nämner alla olika lösningar i enhetscirkeln är att samma värde eventuellt uttrycks av båda uttrycken i den ursprungliga lösningen.
Det verkar inte vara så den här gången.



