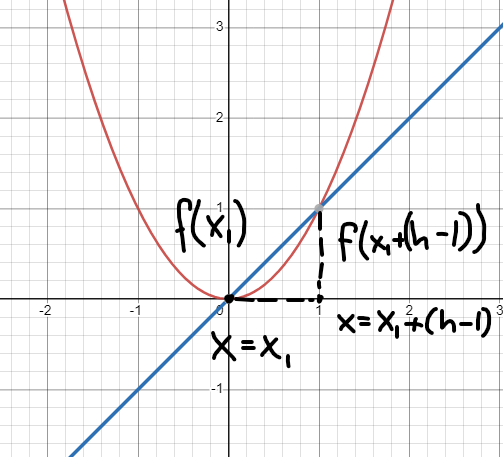varför är det så?
vet inte om jag fattat rätt, men kan någon förklara hur detta kommer sig?
när man ska räkna med derivata så vill man ju ha lutningen i just en specifik punkt (fås genom tangent). Men när man räknar med derivatans definition så blandas det ihop med medellutning? alltså man tar mellan två punkter?
hur går detta ihop? man vill ju ha vid en punkt, måste inte man då ta från själva tangenten och inte från
ex:
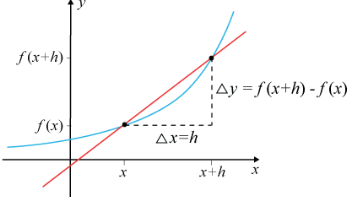
detta är väl en sekant? men detta används vid derivatans definition?
och detta
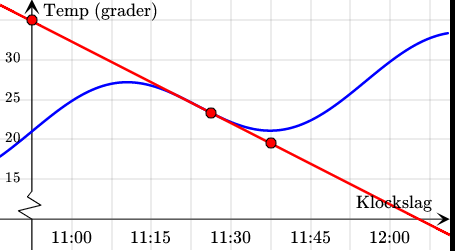
är tangent (derivatans lutning fås ut)
Tanken är att sekanten har tangenten som gränsvärde när h går mot noll.
När h går mot noll tar man sekanten mellan punken x och en punkt som är så nära x att den till slut blir x den också.
jarenfoa skrev:Tanken är att sekanten har tangenten som gränsvärde när h går mot noll.
När h går mot noll tar man sekanten mellan punken x och en punkt som är så nära x att den till slut blir x den också.
vad menar du?
alltså det är alltså för att h går mot noll som sekanten "kan bli till en tanget"?
Säg att vi vill ha reda på lutningen i punkten x=x1. Antag att sekanten skär en annan punkt x=(x1+h). Sekantens lutning kommer då ges av: f(x1+h)-f(x1)(x1+h)-x1=f(x1+h)-f(x1)h. Tänk sedan att h blir mindre och mindre, tills den punkt att det inte finns någon skillnad mellan punkten x1 och (x1+h) i x-led. Då kommer sekantens lutning bli samma som kurvans i punkten x=x1. Vi kan beskriva detta med ett gränsvärde:
limh→0f(x1+h)-f(x1)h
naytte skrev:Tänk sedan att h blir mindre och mindre, tills den punkt att det inte finns någon skillnad mellan punkten x1 och (x1+h) i x-led. Då kommer sekantens lutning bli samma som kurvans i punkten x=x1. Vi kan beskriva detta med ett gränsvärde:
limh→0f(x1+h)-f(x1)h
vad menar du med detta? (inte så inne i det än håller just på att läsa om det) så nu ser det inte så begripligt och bekant ut.
blir den mindre och mindre för att den närmar sig 0?
och detta är jag inte riktigt med på "tills den punkt att det inte finns någon skillnad mellan punkten x1 och ( x1 +h) i x-led. Då kommer sekantens lutning bli samma som kurvans i punkten x= x1. Vi kan beskriva detta med ett gränsvärde:"
Jag ska försöka illustrera det med några bilder. Tänk dig först att vi har en sekant som skär i x=(x1+h) och x=x1:
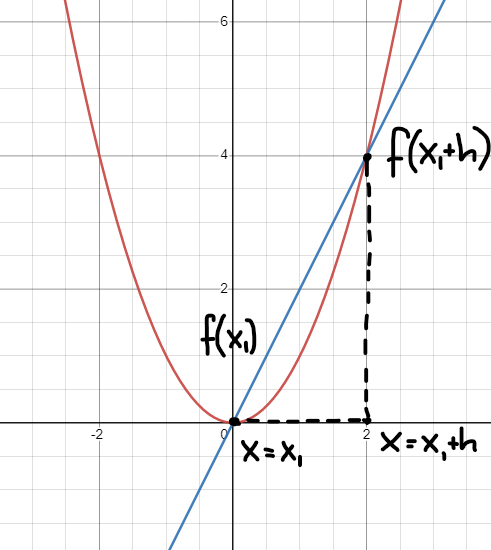
Sekanten har en medellutning i detta intervall som kan beskrivas så: k=f(x1+h)-f(x1)(x1+h)-x1.
Vad skulle sedan hända om vi som skärningspunkt nummer två tar x=x1+(h-1) istället?:
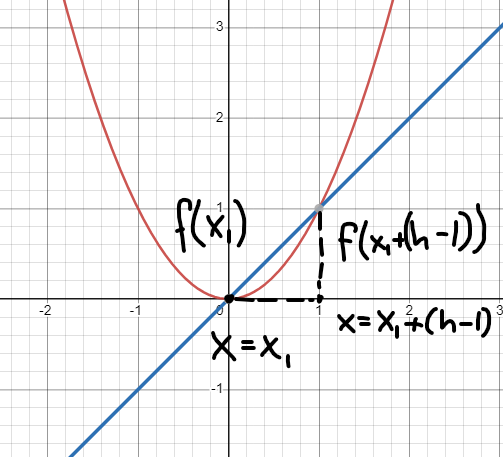
Ser du vad som händer med lutningen på sekanten när h blir mindre?
naytte skrev:
Ser du vad som händer med lutningen på sekanten när h blir mindre?
när h blir mindre så blir lutningen större? eller är det något annat jag bör se?
Tvärtom! Lutningen minskar i det här fallet. Men lite mer generellt kan vi säga att sekantens lutning närmar sig den röda kurvans lutning. Ju mindre h blir, desto likare blir grafernas lutning. När h blir "oändligt litet", kommer sekantens lutning och den röda kurvans lutning vara i princip samma.
naytte skrev:Tvärtom! Lutningen minskar i det här fallet. Men lite mer generellt kan vi säga att sekantens lutning närmar sig den röda kurvans lutning. Ju mindre h blir, desto likare blir grafernas lutning. När h blir "oändligt litet", kommer sekantens lutning och den röda kurvans lutning vara i princip samma.
aha, jo men det är klart den tar ju längre avstånd från y-axeln och då blir lutningen mindre.
det är alltså att ju kortare avstånd = mindre lutning, och detta beror på att h närmar sig 0, om jag förstått rätt?
men det känns som jag inte fortfarande förstått detta
"tills den punkt att det inte finns någon skillnad mellan punkten x1 och ( x1 +h) i x-led. Då kommer sekantens lutning bli samma som kurvans i punkten x= x1. Vi kan beskriva detta med ett gränsvärde:"
h vill alltså komma så nära noll som möjligt så att det bildas en tangent? men varför 0? hur kan det ge ut att "det är avståndet 0?"
och när man sedan räknar ut svaret, vad är det man får fram? är det gränsvärdet så det blir 0?
ursäkta för frågorna men hade uppskattat om någon kunde svara!
Det man får fram när man beräknar gränsvärdet är lutningen till grafen vid en x-koordinat.
h vill alltså komma så nära noll som möjligt så att det bildas en tangent? men varför 0? hur kan det ge ut att "det är avståndet 0?"
När h→0 går f(x1+h)→f(x1).
Du tar fram lutningen i en enda punkt.
"tills den punkt att det inte finns någon skillnad mellan punkten x1 och ( x1 +h) i x-led. Då kommer sekantens lutning bli samma som kurvans i punkten x= x1. Vi kan beskriva detta med ett gränsvärde:"
När h är "oändligt litet" kommer punkten x=(x1+h) ligga "oändligt nära" punkten x=x1. De kommer aldrig vara exakt samma, men de kommer vara så nära varandra att det nästan inte finns någon skillnad. Och om (x1+h)≈x1kommer f(x1+h)≈f(x1).