Var verkar lastens resultant
Hej! Hur ska jag tänka för att räkna ut var resultanten verkar? Q är resultanten, vilken jag får fram genom att integrera q(x) över hela ytan. Längden av ytan kallar jag L. 

Visa spoiler

Hej!
Resultaten måste verka i den punkten som gör att vridmomentet blir detsamma.
Kommer du vidare?
Nej, jag kommer ej vidare. Jag tänkte att jag ev skulle kunna göra en friläggning, men eftersom jag ej vet hur infästningarna ser ut så kan jag ej. Hur ska jag göra?
Jag kan förklara lite mer senare i kväll.
Men facits lösning på uppgift c ger några ledtrådar. Klura på vad dessa två integraler fysikaliskt betyder.
Det hade varit jättesnällt! Okej, jag ska fundera på den.
Såhär tänker jag mig det hela.
Den utbredda lasten, eller kraften per längdenhet, q(x)=q0xL verkar på någon slags endimensionell struktur. Jag ritade för enkelhets skull en stav som struktur.
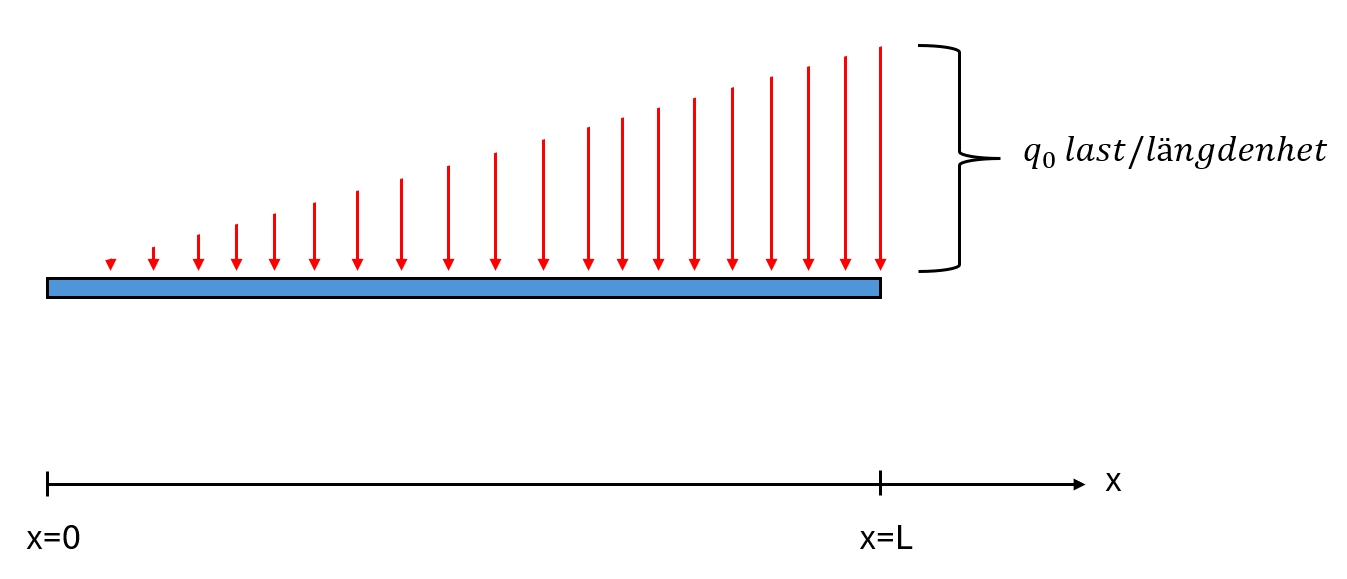
För att man ska kunna ersätta den utbredda kraften med en resultant så måste dels kraftresultanten vara lika stor som den samlade kraften på staven, dels måste denna kraftresultant angripa i en position på staven som gör att vridmomentet på staven är densamma som vridmomentet är från den samlade kraften.
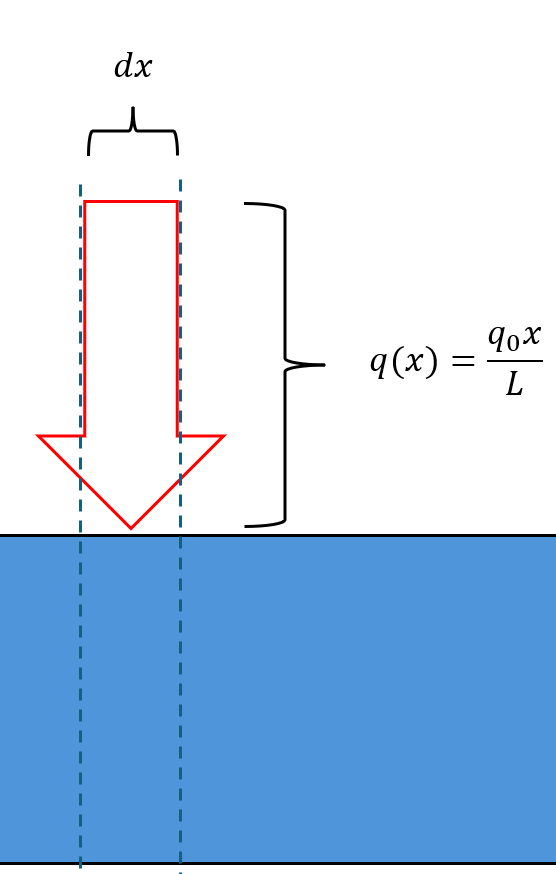
Kraftresultanten har du redan räknat fram genom att titta på hur kraften ser ut på en infintesimalt liten längd dx på staven, och integrera över hela stavens längd, från x=0 till x=L.
Kraften på längdelementet dx blir enligt figuren dF=q0xL·dx, och totala kraften blir därför F=∫dF=∫L0q0xLdx=q0L2
Kan du nu försöka dig på att räkna ut det resulterande vridmomentet på staven (till exempel kring punkten x=0) genom samma resonemang, dvs att titta på det infinitesimala vridmomentsbidraget dM på en liten del dx av stången och sedan addera (integrera) ihop alla små vridmomentsbidrag över hela stångens längd?
Kommer du vidare?
Tack för utförligt svar! Jag får momentet kring x=0 till q0L23. Här är min beräkning:

Men är hävarmen/centrum för kraften då L23? Jag tänker om q0då kanske är kraften?
Bra, du räknade fram det totala vridmomentet från den samlade lasten korrekt.
Om du nu ska kunna skapa ett lika stort vridmoment med hjälp av den resulterande kraften F=q0L2, var på stången måste denna resulterande kraft appliceras?


