Väntevärde
Sitter fast på a) svaret är att
Jag vet dock inte hur man visar det!
Edit: Jag kom fram nu till att man ska använda , men varför ska man betrakta f(x) som kontinuerlig i det här fallet??
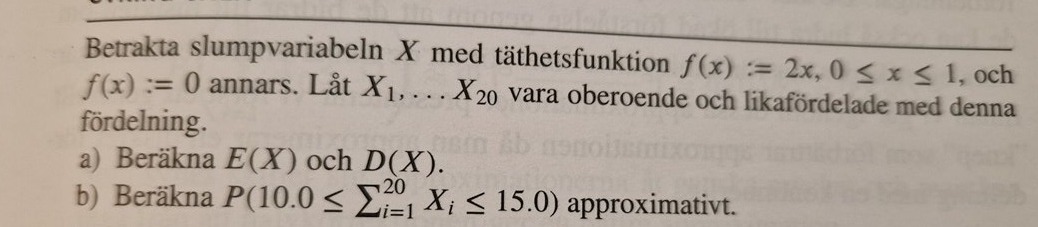
Använd definitionen på väntevärde
E(X) = Integral[ x·f(x)dx ] över R1
Arktos skrev:Använd definitionen på väntevärde
E(X) = Integral[ x·f(x)dx ] över R1
Det har jag gjort om du läser min "Edit" :)
Men frågan är, varför ska man betrakta f(x) som kontinuerlig i det här fallet?
Vad säger du om en likformig fördelning där f(x)= 1 mellan 0 och 1 och för övrigt =0 ?
Det är X som är "kontinuerlig".
En diskret slumpvariabel kan högst anta ett uppräkeligt antal värden.
Kolla exakta definitioner i kursboken.
Arktos skrev:Vad säger du om en likformig fördelning där f(x)= 1 mellan 0 och 1 och för övrigt =0 ?
Det är X som är "kontinuerlig".
En diskret slumpvariabel kan högst anta ett uppräkeligt antal värden.Kolla exakta definitioner i kursboken.
Jag är med på det! :) Fick fram att
på b) Ska jag använda ? Eller finns det andra sätt?
b) Ja, normalapproximation är väl det vanliga. Jag vet inget annat sätt.


