Välj en av 3 dörrar
Läste om ett spel där man kan vinna pengar.
Du får öppna 1 av 3 dörrar, bakom bakom en dörr finns pengar, bakom de andra dörrarna finns 2 getter
Du väljer dörr 1. Innan domaren öppnar din dörr, visar han att dörr 3 har en get
Väljer du nu att stanna kvar på dörrval 1, eller ändrar du ditt dörrval till dörr 2? 
Enligt det jag läste är det större chans att du har rätt ifall du byter dörr.
Förklaring:
I början har du 33,3% chans att få pengarna
I nästa val ifall du byter dörr har du 66,7% chans att få pengarna för då från ursprungliga beslutet en större chans att få pengarna.
Om man väljer att se det som en ny omgång och tänka 50-50 har man fortfarande mindre chans ifall man stannar på samma dörr.
Min egen reflektion är att det egentligen inte spelar någon roll, men om man ska gambla såhär 1000 gånger på raken kanske man bör följa detta exempel och byta dörr. (Gamblar inte, men bara som exempel xD)
Jag googlade lite och jag tror det heter "Monty Hall problem"
Hur ska man tolka detta? Är det bättre att byta dörr eller inte?
Ja, Monty Hall-problemet finns det massor av diskussioner om.
Så här tycker jag är enklast att resonera:
När du väljer första dörren är sannolikheten 1/3 att du väljer pengarna.
Oavsett vad som sedan händer, är sannolikheten att du valde rätt dörr från början 1/3.
Alla andra möjliga utfall måste stå för resten, dvs för sannolikheten 2/3. Om då "alla andra möjliga utfall" är en enda dörr, måste pengarna vara bakom denna dörr med sannolikheten 2/3.
Håller med Bubo, det bästa valet är att byta dörr.
Ett annat sätt att se det på är att expandera problemet. Låt oss föreställa oss 100 dörrar, med getter bakom 99 av dörrarna och ett fint pris bakom 1 dörr. Om du väljer 1 dörr och spelledaren öppnar 98 andra dörrar där det finns getter, skulle du då byta till den sista oöppnade dörren eller stå fast vid den dörren du valde från början? Även om det såklart finns en chans att du valde rätt från början säger intuitionen att det klart är bäst att byta dörr.
Detta kan gradvis skalas ned till färre dörrar, t.ex 50, 20, 10, osv. och för varje variant är det intuitivt bästa valet att byta dörr, om än i mindre utsträckning.
Du dubblerar din vinstchans om du byter dörr. Det var större sannolikhet att du valde fel dörr från början än att du valde rätt, så när spelledaren visar att en av dörrarna har en get bakom sig stiger din vinstchans till 66 % om du byter, eftersom sannolikheten att du valde fel var 33 %.
Det är i princip det Bubo sade uttryckt på ett lite annat sätt.
Har hittat den enklaste förklaringen till varför det är sant nu: 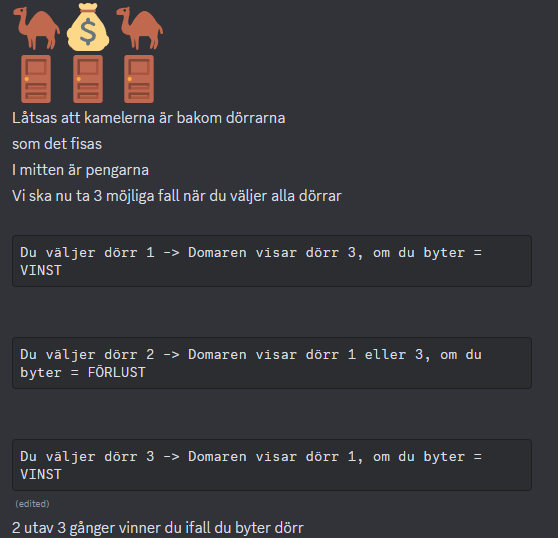 2/3, 66,7%. Enkelt att förstå nu. Ingen kan säga att det inte stämmer nu.
2/3, 66,7%. Enkelt att förstå nu. Ingen kan säga att det inte stämmer nu.
Det spelar ingen roll hur vinsten är fördelad, det blir ändå dessa 3 möjliga utfall
Ingen kan säga att det inte stämmer nu.
Kunde någon göra det innan? 😄
Fundera nu på detta: låt säga att spelledaren inte alls vet var priset är, utan öppnar en dörr helt ovetandes om vad som är bakom. Det visar sig att det inte är priset. Borde du byta dörr?
Jag skulle svara ja. Det spelar väl ingen roll om spelledaren vet eller inte var priset ligger? Bubos argument om utfallsrum borde väl gälla även här?
Jag tänker i samma spår som naytte - antingen har deltagaren valt rätt dörr (1/3), och då spelar det ingen roll vilken dörr som öppnas, utan deltagaren bör inte byta. Eller så väljer deltagaren fel dörr (2/3), varpå spelledaren antingen öppnar dörren utan pris (1/2) eller med pris (1/2). Om spelledaren öppnar dörren med priset bakom sig (1/3), är det självklart att deltagaren bör byta dörr. Om spelledaren öppnar en dörr utan pris (1/3) bör deltagaren byta dörr (i enlighet med ovanstående resonemang). Så det är fortfarande värt att byta i två fall av tre.
Jag vill hävda att Hondels variant leder till att sannolikheten är lika stor att vinna om vi byter dörr som om vi väljer att inte byta.
Jag håller med dig Smutstvätt, men det är under förutsättning att spelledaren kan öppna dörren med priset. Om vi förutsätter att spelledaren öppnat en dörr med en get bakom reduceras utfallsrummet och sannolikheten att vi valt rätt dörr från början är lika stor som om vi valt fel dörr. Alternativt kan vi tänka oss att spelledaren får öppna rätt dörr, men vi betraktar enbart de utfall där vi behöver göra ett aktivt fall (om spelledaren öppnar rätt dörr är det givet att vi ska byta till den, och därmed betraktar vi inte detta utfall).
När jag hörde om det här första gången 1991 (och jag vet inte om det var nytt då) så försökte en del förklara det med en princip som de kallade "restricted choice", som inte definierades strikt. Själv tycker jag det är säkrast att använda grundbegreppen (vilket redan är gjort här, så jag tillför inget).
Calle_K skrev:Jag vill hävda att Hondels variant leder till att sannolikheten är lika stor att vinna om vi byter dörr som om vi väljer att inte byta.
Jag håller med dig Smutstvätt, men det är under förutsättning att spelledaren kan öppna dörren med priset. Om vi förutsätter att spelledaren öppnat en dörr med en get bakom reduceras utfallsrummet och sannolikheten att vi valt rätt dörr från början är lika stor som om vi valt fel dörr. Alternativt kan vi tänka oss att spelledaren får öppna rätt dörr, men vi betraktar enbart de utfall där vi behöver göra ett aktivt fall (om spelledaren öppnar rätt dörr är det givet att vi ska byta till den, och därmed betraktar vi inte detta utfall).
Kan spelledaren öppna dörren som deltagaren valt? Om inte, blir väl utfallet detsamma? Deltagaren väljer dörr, spelledaren öppnar en annan, tom dörr, och deltagaren får välja om hen vill byta. Eller har jag fått något om bakfoten? :)
Jag tänkte nog inte att spelledaren kan öppna deltagarens dörr, men låt oss ställa upp de möjliga utfallen och resonera för var och en av spelvarianterna:
Vi benämner dörrarna med vinstdörr, feldörr1 och feldörr2 (det spelar ingen roll i vilken ordning dessa förekommer). Dessa är de sex möjliga utfall vi har:
- Utfall 1: Vi öppnar vinstdörr, spelledaren öppnar feldörr1
- Utfall 2 Vi öppnar vinstdörr, spelledaren öppnar feldörr2
- Utfall 3: Vi öppnar feldörr1, spelledaren öppnar vinstdörr
- Utfall 4: Vi öppnar feldörr1, spelledaren öppnar feldörr2
- Utfall 5: Vi öppnar feldörr2, spelledaren öppnar vinstdörr
- Utfall 6: Vi öppnar feldörr2, spelledaren öppnar feldörr1
Klassiska Monty Hall
Det enda möjliga utfallen är 1,2,4 och 6. Dessa utfall kommer med sannolikheterna (1/6), (1/6), (1/3) respektive (1/3). Någon skulle kunna hävda att sannolikheterna för de två första utfallen kan viktas annorlunda, men oavsett kommer de summeras till (1/3) vilket är det enda väsentliga för resultatet.
Resultat: Om vi byter dörr har vi (2/3) chans att vinna. Om vi stannar kvar har vi (1/3) chans att vinna.
Monty Hall - Spelledaren öppnar någon av de 2 andra dörrarna slumpmässigt
Nu är samtliga sex utfallen möjliga. I två av sex utfall har vi rätt resultat från början, därmed...
Resultat: Om vi byter dörr har vi (2/3) chans att vinna. Om vi stannar kvar har vi (1/3) chans att vinna.
Notera här att två av utfallen leder till självklara val, dvs om spelledaren öppnar vinstdörren. Om vi bortser från de utfallen, eller ekvivalent antar att spelledaren öppnar en dörr med en get bakom, får vi följande variant av spelet (vilket är det jag tolkar som Hondels variant).
Monty Hall - Spelledaren öppnar någon av de 2 andra dörrarna slumpmässigt, vilket visar sig vara en get
Efter att spelledaren öppnat en dörr med en get bakom utesluts utfall 3 och 5. Eftersom att de andra fyra utfallen har lika sannolikhet kommer dessa viktas om till sannolikhet (1/4) var.
Resultat: Om vi byter dörr har vi (1/2) chans att vinna. Om vi stannar kvar har vi (1/2) chans att vinna.
Låt oss sist undersöka varianten att spelledaren kan öppna deltagarens dörr:
I detta fall har vi 9 utfall, alla med sannolikheten (1/9). I tre av utfallen vet vi med säkerhet vilken som är vinstdörren, varav ett av dessa är dörren vi valt och de två andra är de de två andra dörrarna respektive. I ytterligare 2 utfall vet vi att vi har valt fel dörr, då väljer vi en annan dörr och får rätt med sannolikheten (1/2). För de sista fyra utfallen har vi valt vinstdörren i två av dessa och vi vinner genom att byta dörr för de två andra.
Resultat: Vet vi med säkerhet vilken som är vinstdörren väljer vi denna (1/3 chans att detta inträffar). Vet vi att vi har valt fel dörr byter vi till en annan (2/9 chans att detta händer, med sannolikhet 1/2 att vinna). För resterande fall spelar det ingen roll om vi byter eller inte (4/9 chans att detta inträffar, med 1/2 chans att vinna.)
Sammantaget 1/3 + 1/9 + 2/9 = 2/3 chans att vinna.
Tillägg: 13 maj 2024 14:07
Antar vi att spelledaren öppnat en feldörr i den sista spelvarianten (eller ekvivalent att vi bortser från de säkra valen) kommer de tre förstnämnda utfallen uteslutas. De sex resterande utfallen kommer viktas om och sannolikheten att vinna blir 1/6 + 2/6 = 1/2
Väl sammanställt! 😊
Smutstvätt skrev:Väl sammanställt! 😊
Lyckades jag få över dig på min sida? :D
Jo men det tycker jag! Skillnaden låg i tanken om att vi står och tittar på geten, dvs. att vi inte behöver ta hänsyn till utfallet där spelledaren slumpar fram vinstdörren, då slumpvalet redan har skett (till vår nackdel). Jag tänkte på ett scenario där vi tänker på hela spelet innan det börjar. Kan då spelledaren öppna vinstdörren måste det då tas med i beräkningen. Men det gör vi inte, så det känns grönt. :)
Jag provar med Bayes sats. Först den ”vanliga” varianten när spelledaren vet var priset är.
Låt D vara händelsen att priset är bakom min dörr jag precis valt. Låt M vara händelsen att spelledaren, som kallas för Monty Hall, visar en get bakom sin dörr.
Vi vill räkna ut P(D|M)=P(M|D)P(D)/P(M) enligt Bayes sats.
P(M|D)=1
P(D)=1/3
P(M) = P(M|D)P(D) + P(M|D^c)P(D^c) = 1* 1/3 + 1 *2/3 = 1 (lagen om total sannolikhet, D^c är komplementhändelsen till D, jag sitter på mobilen så tidsödande att formatera)
Sammanställer vi detta får vi
P(D|M) = 1*1/3 / 1 = 1/3 så det är alltså bara 1/3 att priset är bakom din dörr, och därmed 2/3 att den är bakom den andra dörren. Bättre att byta alltså.
Låt nu Monty vara helt omedveten om var priset är. Man kan återvinna allt jag gjort ovan, förutom en term: P(M|D^c). Eftersom Monty inte längre vet var priset är kommer inte denna vara 1 längre, utan 1/2: han har två dörrar att välja mellan och en av dem har en get. Därmed blir P(M) = 1*1/3 + 1/2 * 2/3 = 2/3 och hela uttrycket
P(D|M) = 1*1/3 /(2/3) = 1/2, dvs, det spelar ingen roll om du stannar eller byter, det är 50/50.
Faktum är att om vi generaliserar detta till att det finns N stycken dörrar, man väljer en och sedan öppnar Monty alla utom den du valt och en till och alla han öppnat har getter bakom sig är det fortfarande 1/2 att priset är bakom din dörr. Känns spontant ganska otroligt tycker jag, men man ska komma ihåg att detta är alltså en betingad sannolikhet, vi vet att det bara är getter bakom dörrarna Monty öppnat, men om han inte vet var priset är kommer det i många fall vara så att han råkar öppna en dörr där priset är (men det är alltså inte en situation vi är intresserade av)






