ta fram asymtoten
Jag håller på med assymtoter och tror mig förstå grunden till lodräta och sneda asymtoter, men förstår inte hur jag ska bevisa det matematiskt.
Horisontella asymtoter känner jag mig helt lost kring. Jag vet att man ska se vilket y-värde grafen går mot när x närmar sig oändligheten, men kan inte förstå hur jag ska ta fram det. Jag ser liksom inte logiken i ett tal som är oändligt stort/litet
Sned asymtot: JAg vet att täljarens gradtal måste vara en mer än nämnarens gradtal och att man sedan utför polynomdivision eller delar upp termer på ett liknande sätt som detta:x3-2x2+4xx2 , den sneda asymtoten är x-2, men varför försvinner bara 4/x?
Hur skulle jag undersöka om det finns en vågrät asymptot för denna graf?
kan denna tråd ge ngn ledning?
För vertikala undersöker du ändpunkter i intervall eller där funktionen inte är definierad. Om funktionen går mot + eller -oändligheten när x rör sig mot denna punkt existerar en vertikal asymptot där.
Ture skrev:kan denna tråd ge ngn ledning?
Det kanske är gränsvärdet jag inte förstår hur jag ska räkna med eftersom jag fortfarande inte förstår. Jag förstår liksom en del av det, men itne tillräckligt för att kunna applicera det på en uträkning. Tittat på otaliga videos, men förstår fortfarande inte alls och när jag tror att jag förstår förvirrars det ihop direkt efter....
aha
om vi tar exemplet i din tråd
x-2+4/x när x går mot oändligheten blir x större och större, medans 4/x blir mindre ju större x är.
När vi närmar oss oändligheten närmar sig 4/x noll.
Om vi ritar funktionen 4/x ser den ut så här
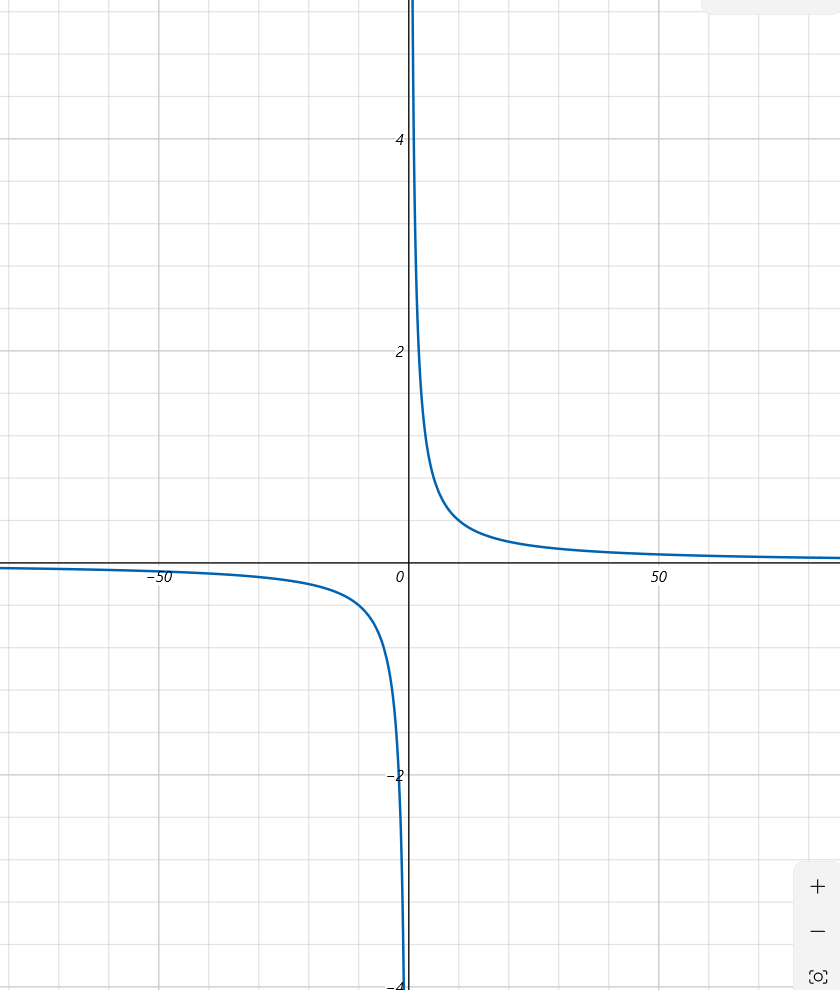
Vi ser att y närmar sig +0 när x går mot oändligheten och mot -0 när x går mot - oändligheten.
Jämfört med x+2 bidrar alltså 4/x inte mycket (läs: inte alls) när x är stor.



