Vågor som kommer ikapp tidigare vågor
Hej!
I min bok står det så här:
"En annan följd av att vågor bromsas in på allt grundare vatten är att vågorna bakom hinner i fatt vågorna framför så att de reser sig och kan bilda kammar."
- Vad menas egentligen med att de kan bilda "kammar"?
- Eftersom frekvensen är oförändrad, hur kommer senare vågor ifatt tidigare vågor?
Tack på förhand!
Det handlar säkert om vattenvågor.
Vattenvågor är komplicerade. Utbredningshastigheten beror på våglängd och på vattendjupet.
Men då kan man får sådant här: https://commons.wikimedia.org/wiki/File:Mavericks_Surf_Contest_2010.jpg
https://commons.wikimedia.org/wiki/File:Mavericks_Surf_Contest_2010.jpg
Ja, precis, det är i kapitlet om vattenvågor! :)
Frågan återstår: om frekvensen är oförändrad vid refraktion, hur kan vågor komma ikapp?
När våglängden ändras (och det kan den göra om vattendjupet ändras) så måste utbredningshastigheten ändras.
Hmm, jag hänger med på att våglängden blir kortare när vattendjupet blir grundare, och att utbredningshastigheten då sjunker.
Men, frekvensen är ju oförändrad - dvs att det fortfarande passerar X antal vågor på en punkt vid 1 sekund? Hur kan då senare vågor komma ikapp?
Majskornet skrev:Hmm, jag hänger med på att våglängden blir kortare när vattendjupet blir grundare, och att utbredningshastigheten då sjunker.
ökar.
Men, frekvensen är ju oförändrad - dvs att det fortfarande passerar X antal vågor på en punkt vid 1 sekund? Hur kan då senare vågor komma ikapp?
Det är en bra fråga. Ofta kan man tänka likadant på vattenvågor som på ljusvågor, men det funkar inte riktigt här. Ljusvågor kan aldrig komma ikapp, enligt precis de principer som du nämner.
Med vattenvågor är det en del massa som ska tryckas upp och ner, så trögheten i vattenmassan kan nog "smeta ut" vågrörelsen så att vågorna går i varandra om de är tillräckligt nära. Någon sorts interferensliknande effekt, som beror på (åtminstone delvis, tror jag) vattnets tröghet.
Har Pieter någon bättre kunskap om det här? Eller någon annan?
Majskornet skrev:Men, frekvensen är ju oförändrad - dvs att det fortfarande passerar X antal vågor på en punkt vid 1 sekund? Hur kan då senare vågor komma ikapp?
Det är bra tänkt. Även vid en långgrund kust mäter man samma frekvens som vågorna uppstod med ute på havet. Hastighetsberoende på djupet gör bara att vågorna kommer in alltid parallellt med stranden. Detta med kammen uppstår för att våglängden blir kortare när vågen går långsammare. Då måste vågen bli högre (mängden vatten är konstant), tänk också på tsunamin. Tills den bryts.
Detta med att komma ikapp kan man se om man kastar en sten i vatten. Då är det en puls som blir ringar av vågor som utbreder sig cirkulärt. Och då kan man se att vågor närmare mitten kommer ikapp vågor längre ut och komma förbi dem. Något som man kan roa sig med när det blir bättre väder.
Tack för svaren!
Hur kan man förklara fenomenet med den konstanta frekvensen i åtanke?
Majskornet skrev:
Hur kan man förklara fenomenet med den konstanta frekvensen i åtanke?
När man kastar en sten i vattnet uppstår en puls och den kan betraktas som en summa av många vånglängder och frekvenser.
Hmm, okej, så egentligen kan bara vågor komma ikapp tidigare vågor om det inte är en konstant frekvens?
Majskornet skrev:Hmm, okej, så egentligen kan bara vågor komma ikapp tidigare vågor om det inte är en konstant frekvens?
Det tror jag att det stämmer. Det är nog bara vattenvågor med olika frekvenser som kan komma ikapp varandra och då passerar de genom varandra. Och det är förstås vanligt att det finns många frekvenser.
Om det bara finns en frekvens (t ex dyningen som uppstår efter en långvarig storm på oceanen) då kommer vågorna inte ikapp varandra. Detta med kammar förklaras nog bättre med den här bilden: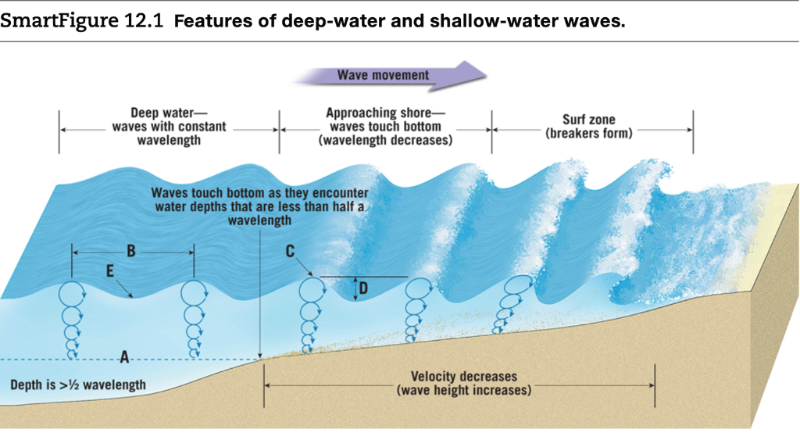
Pieter tänker som vanligt klarare och bättre.
Ett spektrum av olika frekvenser vid t.ex. ett stenkast tänkte jag inte alls på. Om vattnets tröghet har någon betydelse är den nog mycket mindre än de övriga orsakerna som Pieter nämner.
Tröghet är nog alltid viktig vid mekaniska vågor. Och jag tror att vattnets tröghet är särskilt viktig för att förstå varför vågen bryter, att vågens topp fortsätter med sin hastighet när vågens bas bromsas.
Men vattenvågor i djupt vatten är redan komplicerade (inte rent transversella, inte longitudinella, vattnets rörelser kan beskrivas med cirklar). Det blir mer komplicerat i grunt vatten. Och när vågen bryts blir det nog rätt hemskt att räkna på.
Jag har inte tänkt tidigare på varför en vågkam heter så, men man kan nog jämföra med en tuppkam. På engelska kan tuppkam tydligen heta både comb och crest, och vågkam heter ju "crest of a wave".
Jag kan tänka mig att de egentligen inte menade "komma ikapp" i texten utan bara komma närmare.
Tack för alla svaren och för bilden, nu förstår jag mycket bättre!




